Introduction to Googology

Last year CFY suddenly became interested in “googology” and “ordinals”, and even recommended an “ordinal incremental” game Ordinal Markup to me, and then I unfortunately fell into the rabbit hole. 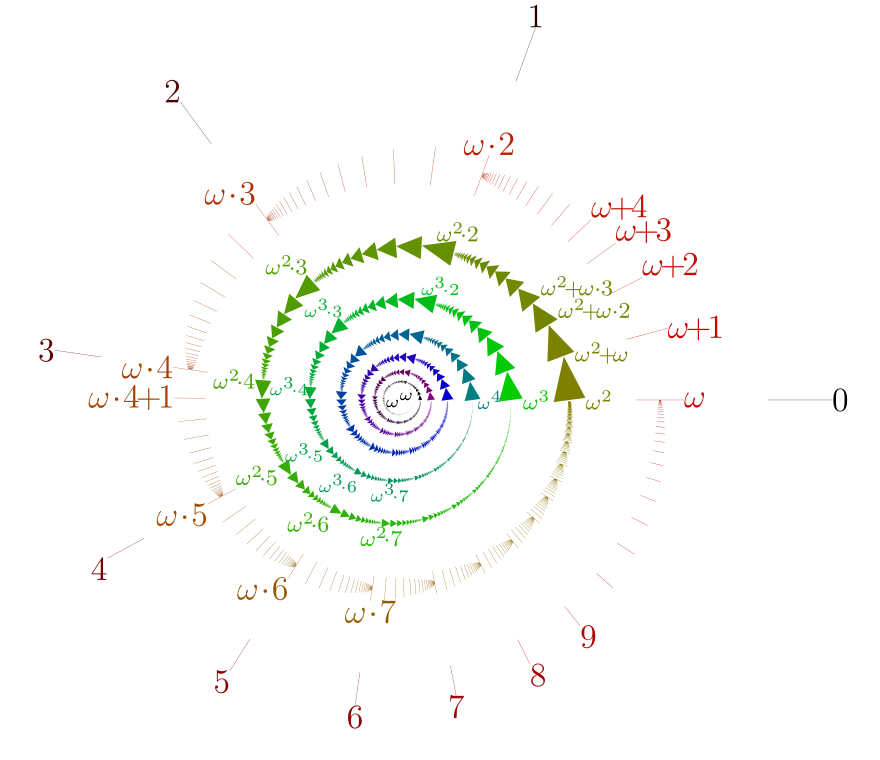
I had heard about ordinals a long time ago, but I always felt these things beyond infinity were too abstract, and I wasn’t interested in understanding them deeply at the time. Later I discovered this topic was more interesting than I imagined.
Note: Since there are many googology tutorials online, this article only serves as an introduction and won’t explain specific details in depth.
What is Googology?
“Googology” studies how to describe numbers as large as possible. If you think this is simple, you’re being too naive. The large numbers these people study are far beyond any imagination: the number of zeros after the number of digits of the number of digits of these numbers is so large that even if you filled the entire universe with notebooks, you couldn’t write them all down. In fact, even for the number of digits of the number of digits of the number of digits… of the number of digits of the number of digits to become small enough to reach numbers we commonly encounter, if you tried to expand that ellipsis and write it out, all the paper in the universe still wouldn’t be enough! Although these numbers are enormous, they are all finite. In this game of who can describe the largest number, absolute infinity is prohibited from participating.
Systematically describing these numbers generally uses iteration methods. For example, the first-level operation addition is actually the iteration of the zeroth-level operation successor (successor means counting one more number, equivalent to adding one), the second-level operation multiplication is the iteration of the first-level operation addition, the third-level operation exponentiation is the iteration of multiplication… This can be uniformly written as: $a\uparrow^n b$ represents the $n$-th level operation between a and b. Don’t think it stops here. We can continue nesting: let function $f(n)=3\uparrow^n 3$, nesting the operation level 64 times, we get a ridiculously large monster $f(f(f(f…f(f(3))…)))$, called Graham’s number, which comes from an upper bound of a mathematical problem’s answer. However, this is just the beginning of googology. Other interesting large numbers include Tree(3), Rayo’s number, Loader’s number, Busy beaver, etc., all introduced in this article.
If you want to continue learning about googology, you can refer to the links at the end.
Enter the Ordinals
Now let’s talk about the protagonist of googology—ordinals. Ordinals are things between finite natural numbers and absolute infinity, extensions of natural numbers. Ordinals are not some pseudoscientific concept; they are rigorously defined in the recognized mathematical foundation axiom system—ZFC set theory. In set theory, each natural number is a set that consists of all numbers smaller than it, and zero is the empty set:
$$0=\left\{\right\}=\phi$$$$1=\left\{0\right\}$$$$2=\left\{0,1\right\}$$$$3=\left\{0,1,2\right\}$$$$…$$Observing carefully, we find $x+1=x\cup\left\{x\right\}$, for example $5=\left\{0,1,2,3,4\right\}$, $6=5\cup\left\{5\right\}=\left\{0,1,2,3,4,5\right\}$
The set of all natural numbers $\left\{0,1,2,3,….\right\}$ is certainly no longer a natural number, but if we forcibly treat it as a number, we can transcend infinity and continue counting upward—these are “ordinals”. Let $\omega=\left\{0,1,2,3,….\right\}$ then$$\omega+1=\omega\cup\left\{\omega\right\}$$This way we have$$\omega+2$$$$\omega+3$$$$…$$And the number containing all the above ordinals is called $\omega+\omega$, also written as $\omega2$. Continuing this expansion leads to $\omega3$, $\omega4$, until the limit $\omega^2$, then continuing to $\omega^2+1$, $\omega^2+\omega$, $\omega^2 2$, $\omega^3$ and so on. We see that an ordinal is either a successor ordinal: obtained by adding one to an ordinal, or a limit ordinal: obtained by encompassing infinitely many previous ordinals. Although limit ordinals exist, just like natural numbers, there is never a largest ordinal: just add one to it.
Optional reading: Continuing this enumeration reaches $\omega^\omega$, $\omega^{\omega^\omega}$. Perhaps you think the next ones would be $\omega\uparrow^4 \omega$, $\omega\uparrow^\omega \omega$, $\omega\uparrow^{\omega\uparrow^\omega \omega} \omega$ etc., but due to infinity, many operational rules between ordinals differ from natural numbers. For example, addition and multiplication no longer have commutativity ($2\omega$ means adding $\omega$ twos together, the limit is still $\omega$; adding two $\omega$s gives the larger $\omega 2$), so we can’t generalize to the fourth-level operation after exponentiation. Beyond this, we can only continue by introducing many fixed points of exponential tower iteration, fixed points of fixed points of fixed points… For details, see the Veblen $\varphi$ function in the ordinal tutorials linked later.
What are ordinals useful for? They can be used to describe functions with astonishingly large growth rates and thus represent large numbers, namely various “growth hierarchy functions” of different speeds. See the links later for details. Ordinals are also a ruler for measuring the growth rate of large number functions. It can be said that to master googology, ordinals are the most basic and important tool. For example, that “Graham’s number”, expressed using the fast-growing hierarchy (FGH) function is merely $f_{\omega+1}(64)$. Why is the ordinal corresponding to such a large number so small? Simply put, the nesting times of these iterative functions can correspond to ordinals through certain methods. For example, addition comes from continuous iteration of successor (i.e., one “nesting”), so its growth rate corresponds to ordinal 1, multiplication to 2, the n-th level operation to n. But if the function’s argument is the operation level n itself, like $f(n)=3\uparrow^n 3$, its growth rate naturally exceeds all functions with natural number nesting times, and here the ordinal $\omega$ that exceeds all natural numbers comes to the rescue. When we construct Graham’s number, we perform another nesting on this operation level n, thus corresponding to ordinal $\omega+1$. It’s conceivable that continuing to nest can yield larger successor ordinals, and then if we make the nesting times the function argument, we get limit ordinals, and then we can continue endlessly nesting. The growth rate of large number functions, like ordinals, has no end… For precise definitions and analysis of these growth rates, see this article.
The “cover image” at the beginning of this article shows how fast-growing sequence functions nest: 
In my opinion, it is precisely because ordinals can serve as a ruler for measuring the growth rate of large number functions that ordinals, this abstract mathematical concept, has practical “down-to-earth” uses, rather than being just a useless toy defined in set theory that transcends infinity. What use is googology itself? Besides what everyone can think of—mathematicians doing research for entertainment—I also heard this story:
I studied a lot of mathematical logic and set theory in my freshman year and high school, always thinking this was the hardest to write and least useful mathematics in science fiction. But even this can be used, and unexpectedly it’s quite popular, because those people like to debate, comparing battle power levels, how to compare sizes… In the end, they can only resort to ordinal theory, cardinal theory…
I must say this use of googology is truly unexpected.
Collection of Resources on Large Number Theory
If you want to continue learning about large ordinals in depth, you can refer to the following links:
Popular Science
- Matrix67’s blog post introduces tetration and other operations in detail, mentioning that $100\uparrow^{100} 100$ is already casually far far…….far larger than the number of all possible arrangements and combinations of particles in the universe.
- List of large numbers on Googology Wiki
- Youtube video listing large numbers from 1 to infinity (9 hours 54 minutes long)
- Codeparade’s (the author of 4D Golf!) “Finding the Largest Number” video
- A small story about ordinals written in the style of GEB‘s turtle and Achilles dialogue (unfortunately I can’t find the Chinese version I first read, the original is in French)
Tutorials
- Cao Zhiqiu’s “Large Number Theory” (dynamically updated): The most comprehensive and systematic Chinese textbook on googology to date, bar none. (If the GitHub link doesn’t work, here’s a cloud drive link (240807 version))
- core.exe’s ordinal tutorial on Zhihu, very detailed, covering n-th level operations, fast-growing hierarchy, ordinals, Veblen functions, OCF, reflection and other concepts.
- Suzuka Meiten’s ordinal tutorial on Zhihu, covering concepts like Prss, BMS, reflection, stability, Y-sequences.
Tools
- Naruyoko’s googology-related calculation tools: Including BMS and 0-Y sequence converters, mountain diagrams for various Y-sequences, online fundamental sequence calculators, etc. He has also implemented online calculators for many large number notations I’ve never heard of.
- Ordinal Browser, highly recommended, can arbitrarily expand fundamental sequences of limit ordinals, and you can choose your preferred ordinal representation.

![Ordinal Browser settings to represent everything using "0", "[c]" (equivalent to $\Omega$), "+" and BOCF $\psi$ function](/img/ord003.png)
- My own Ordinal Map, similar to Ordinal Browser, but uses a more visual method to display ordinals: just zoom like an online map to find all ordinals (currently maximum ordinal reaches EBO, supports BOCF/MOCF and Veblen representation, may plan to support recursively inaccessible ordinal I etc. in the future), no need to click any expand buttons.
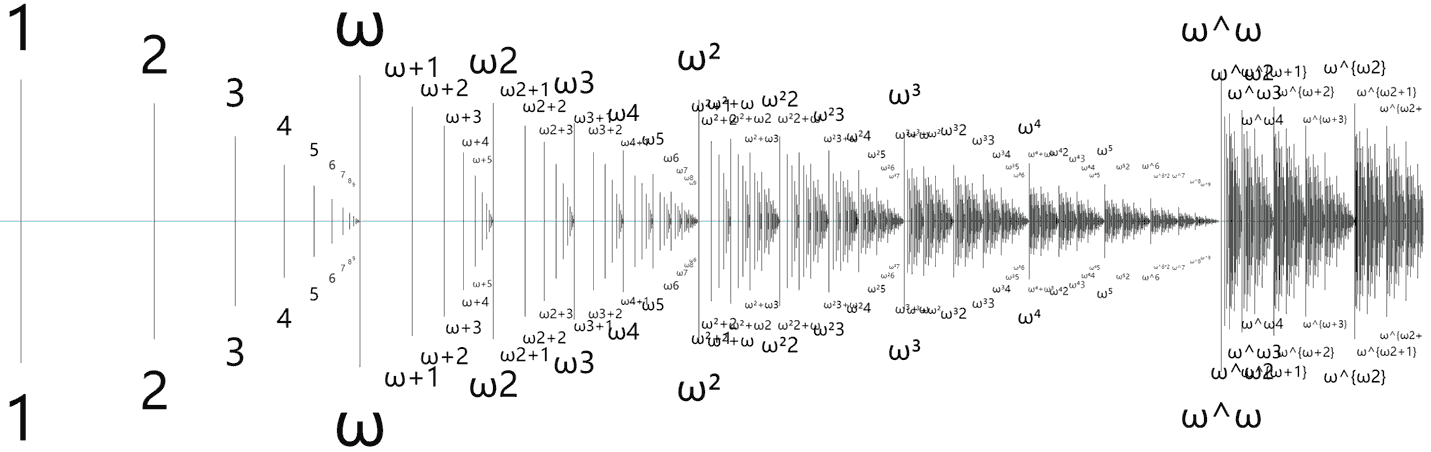
Operation tips:
- Mobile: Drag blank areas to pan the map, click plus/minus to zoom. Hold plus/minus and slide right to accelerate zooming.
- Desktop: Click and drag to pan the map, scroll wheel to zoom, press T/G keys to adjust zoom rate, press W/S keys to adjust iterative rendering depth.
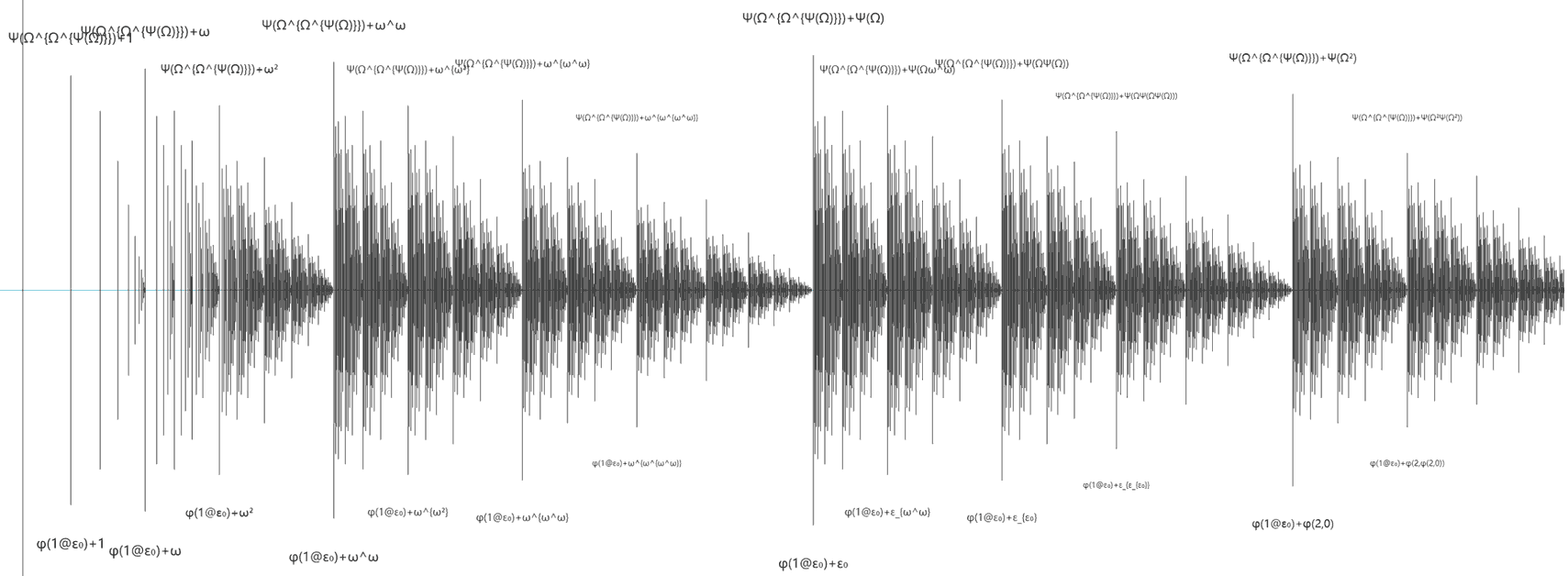
Non-recursive Ordinals
Ordinals are like a cheat code existence. If you think you can get all ordinals just by continuously taking successors and limits, you’re wrong. Non-recursive ordinals are defined as numbers that cannot be obtained through nesting fewer times than themselves. Thus we cannot construct non-recursive ordinals from bottom up. In ordinal collapsing functions, we encounter the non-recursive ordinal $\Omega$, which can be used to generate smaller recursive ordinals, very similar to generating finite large numbers through fast-growing hierarchy functions and infinite ordinals. The following diagram shows the relationship between the three levels of large numbers, recursive ordinals, and non-recursive ordinals: 
Cardinals and Ordinals
It should be noted that there’s another concept called cardinals, which is similar to ordinals. Both describe things beyond infinity, but they are very different. Cardinals have no hierarchical structure; they simply measure how many elements are in infinite sets through whether bijections can be established between sets. Ordinals and cardinals can be converted: ignoring the order structure of ordinals and just looking at the set size converts ordinals to cardinals, and given a cardinal, the smallest ordinal with elements equal to that cardinal is the ordinal obtained from that cardinal conversion. The ordinals introduced earlier, although very large, even reaching BHO, EBO or even Y-sequences, are all still countable, meaning they have as many elements as natural numbers. Their cardinals are all the same size, denoted $\aleph_0$. (Note: Non-recursive ordinals can also be countable, but uncountable ones must not be recursive ordinals) With $\aleph_0$, the next larger cardinal is $\aleph_1$, $\aleph_2$…$\aleph_\omega$…, since cardinals can also be treated as ordinals, naturally we have $\aleph_\omega=\aleph_{\aleph_0}$, then we have $\aleph_{\aleph_{\aleph_{…}} }$… The famous continuum hypothesis states that there is no cardinal between the number of real numbers ($2^{\aleph_0}$) and the number of natural numbers ($\aleph_0$), i.e., assuming $\aleph_1 = 2^{\aleph_0}$. The continuum hypothesis is independent of ZFC set theory, meaning you can choose to believe it’s true or false, and the theories built respectively won’t contain contradictions.
After playing ordinal games for a long time and reading a lot about set theory, I suddenly wanted to know what exactly is ZFC set theory, the foundation of ordinal theory? By the way, the later methods for constructing large ordinals like reflection ordinals, stable ordinals, etc. need to be defined in set theory. Besides stacking various large ordinals, we can also continue stacking large cardinals. To understand these things, we must dive into the rabbit hole of mathematical logic and formal systems, which we’ll fill in the next article.
Suggested Learning Sequence for Ordinals
- Start with ordinal addition, multiplication, and exponentiation, understand $\varepsilon_0$,
- Understand the fixed point iteration pattern, understand $\varepsilon_1$, $\varepsilon_\omega$, $\varepsilon_{\varepsilon_{\varepsilon_{…}}}$, binary to multi-ary Veblen functions.
- Start learning ordinal collapsing functions OCF (note there are two different versions, MOCF and BOCF, beginners can choose one), understand the recursive ordinal BHO.
- Learn OCF containing the second non-recursive ordinal $\Omega_2$, up to $\Omega_{\Omega_{\Omega_{…}}}$, understand the recursive ordinal EBO.
- Learn I/M/K/reflection ordinals, learn stable ordinals, Y-sequences, etc.
Since I’m still at the stage of learning reflection ordinals, I can’t provide further ordinal learning plans. Please refer to the articles by the experts on Zhihu mentioned above. So many complex ordinal notations are really maddening. I personally suggest at least knowing and understanding ordinal collapsing functions (OCF), after all, this appears even in that ordinal game. I’ve spent many half-days stacking OCF ordinals on paper… If you still think OCF is too simple and the ordinals produced aren’t large enough, then go challenge reflection ordinals, stable ordinals, Y-sequences and such. Let me mention Y-sequences here (0-Y sequence ordinal map link). It’s an incredibly powerful family of ordinal notations, with different versions like 0-Y, 1-Y, $\omega$-Y sequences. All the ordinals obtained from continuously strengthening through Veblen, OCF, reflection, and stable notations, their growth rates are instantly obliterated to nothing in front of the Y-sequence family (even in front of the mildest growing 0-Y), absolutely terrifying…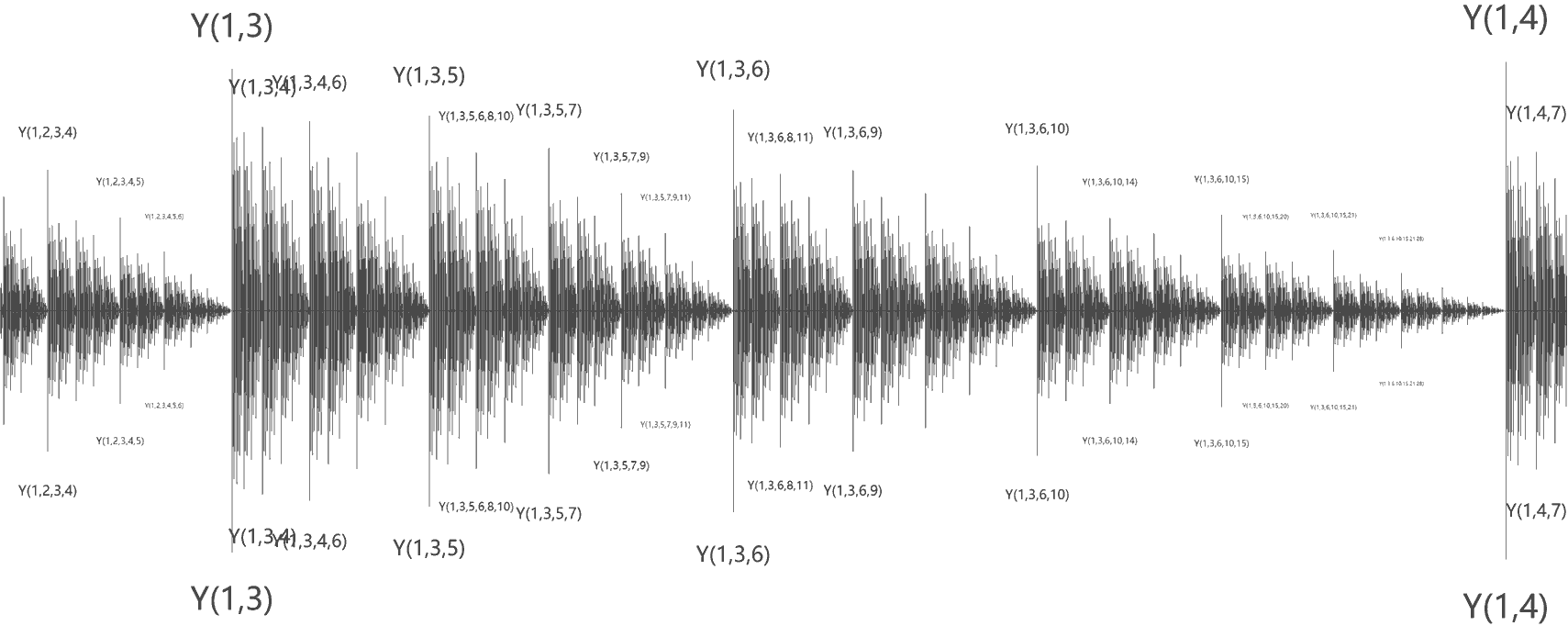
p.s. Originally CFY wrote some draft articles introducing ordinals and planned to make an “ordinal laboratory”. I thought I’d put a link here to save him a spot, but his envisioned ordinal laboratory would implement almost all mainstream representation methods including Veblen, OCF, reflection, stability, Y-sequences, which seems quite difficult. I wonder if it will end up abandoned…
Ordinal Markup and Incremental Games
Finally, let’s talk about the game Ordinal Markup. The game starts with clicking a button to increase the ordinal by one, then buying auto-clickers and various upgrades, making the ordinal grow faster and faster. You also need to complete many specified challenges to get achievements, etc. I won’t spoil the specifics. The game is very time-consuming. In the late game, sometimes you need strategy plus long idle time to reach the next level. Currently both CFY and I are stuck at the singularity function level, and after getting 60 achievements, we haven’t made progress for several months. (I think I started playing in October 2023)
If you find the game too difficult, you can play an easier version Ordinal Markup FSE (Factor Shift Edition). This version can be completed within a few days. If you’re interested in incremental games, you can also try:
- Another game by the same author Time Layers, I got stuck at the galaxy part;
- Derivative Clicker, which originally inspired the author.
- The more polished cookie-making game Cookie Clicker. (I saw this recommendation in “Large Number Theory”, but it’s actually unrelated to large numbers, purely a casual incremental game)
Well, that’s all for the introduction to ordinals/large number theory. In the next article, we’ll look at the foundation of googology and even mathematics: formal systems and ZFC set theory.