This article is a continuation of “Visiting the Four-Dimensional Country”. In that article, I mentioned that 4D urban traffic doesn’t need overpasses because the ground is three-dimensional, and traffic flows in two directions only need to follow skew lines. Now let’s first study what roads in the 4D country actually look like, how cars drive on them, and the analogues of tricycles and bicycles in four-dimensional space. To study general objects in 4D, we can’t use stereographic projection, because stereographic projection essentially studies hyperspheres - we need to project regular polytopes onto hyperspheres. So we’ll start with the cross-section method and projection method. First, let’s look at a straight road with curbs in 3D: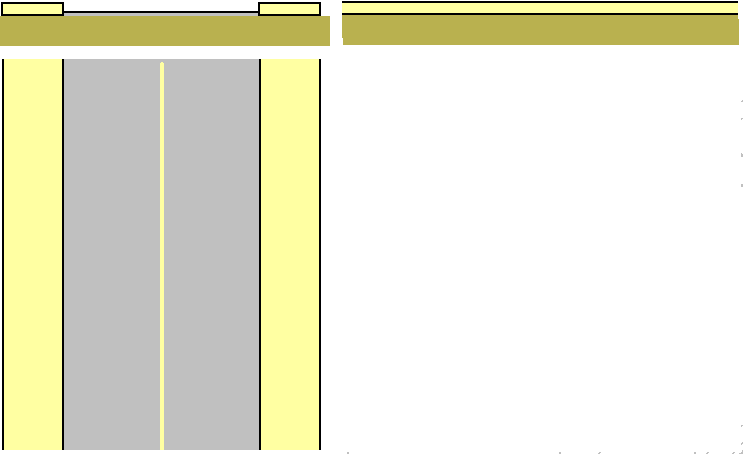 
We see that the top view is the clearest, except that you can’t see the height of the curbs. What about 4D roads? Their top view is a three-dimensional cylindrical shape, but should the base be square? Or circular to make the road cylindrical?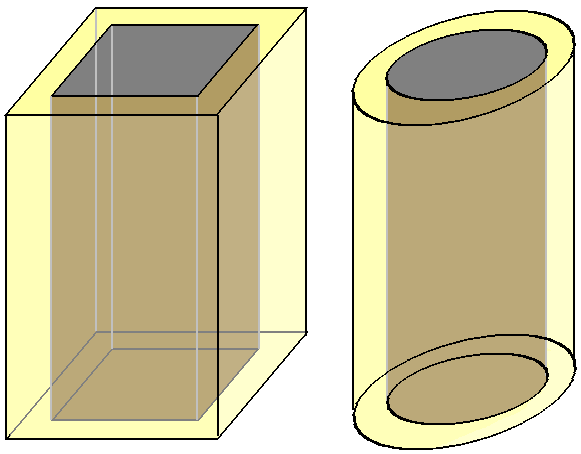 
We see that due to the extra dimension, the question of the road’s 2D cross-sectional shape becomes meaningful (there’s only one type of one-dimensionally connected figure: a line segment). Note that I drew the road as transparent only for observational convenience. Actually, 4D people can directly see 3D images without obstruction - they would see each point on the curb as uniformly light yellow, and the road surface as uniformly gray. 4D people don’t need to cross the road - they can just go around from the curb! Note this isn’t climbing over or building an overpass, because this is a top view, and gravity is perpendicular to all directions in the projection. What if there are no curbs? Would they then have to cross the road? Actually, no. Vehicles are concentrated in the cylindrical shape, so you just need to walk around the edge and you’ll be fine (though with some risk). So which is better - roads with square or circular cross-sections? How should lanes be divided (like whether there should be a line in the middle)? These two questions are actually related, and we’ll discuss them later.
Four-Dimensional Wheels
Before discussing this issue, let’s first look at the shape and construction of cars. In a 2D world, cars need two wheels (though it seems impossible to fix the wheels to the car). 3D cars need four wheels: (let’s not consider other vehicles with fewer wheels for now)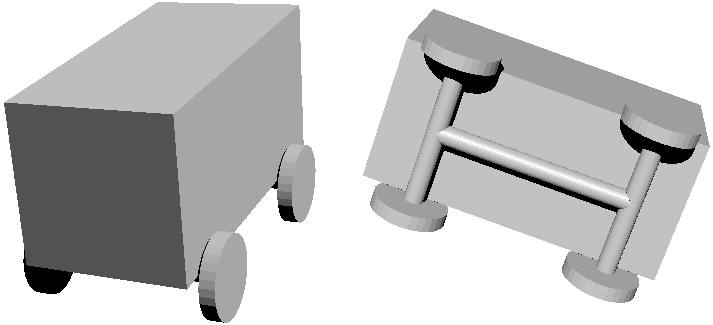 
We see that the car body is placed on a chassis that connects four wheels. Like the hypercube analogy, we naturally think that 4D cars need eight wheels, distributed at the vertices of a rectangular solid, while the car body above can be approximated as a hyperrectangular solid. Let’s look at the top view of a 4D car: But the hyperrectangular car body above would block the chassis structure below, so let’s first look at the chassis structure separately. But here we have a serious problem: the shape of the tires. As I analyzed in “Visiting the Four-Dimensional Country”, to control the car’s movement, tires can only have one direction of rolling freedom (for example, in our world, no car has spherical wheels). This shape is a cylinder (actual tire cylinder edges are smooth, so they should be considered toroidal, but let’s not consider this for now). But in 4D space, cylindrical shapes form a family: common ones include the cubinder (cylinder-cylinder) and the duocylinder (direct product of two circles). We face the same problem as choosing road cross-sections. Let’s place them sideways on a 3D plane and see how they roll from a top view: First, we need to understand how to place them “sideways” to make them roll. For example, a cylinder placed upright (circular face down) can’t roll, so the circular base of a cylindrical shape can’t face down - it must be sideways. Looking at the cylinder’s height, it’s a line segment (like the gray line on the left in the figure below). In 4D, the cubinder has two heights forming a square, but this side figure can be arbitrary - if we take a circle, it’s called a duocylinder. The duocylinder’s base and side are symmetrical, so it can roll no matter how it’s placed, but the principle is the same as the cubinder - it can only roll in one direction. 
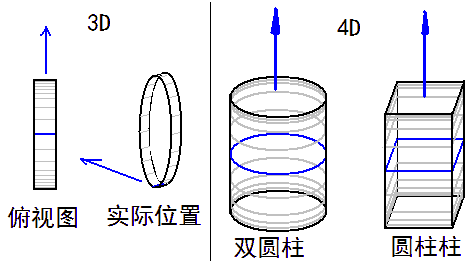Which type of tire is better? Actually, the shape of the side height doesn’t participate in rolling, so any shape is fine. But considering that real tire cylinder edges are smooth enough to be almost toroidal, I think choosing the duocylinder with fewer edges is better.
With preparations complete, let’s now construct the 4D car’s chassis. Its top view looks like this: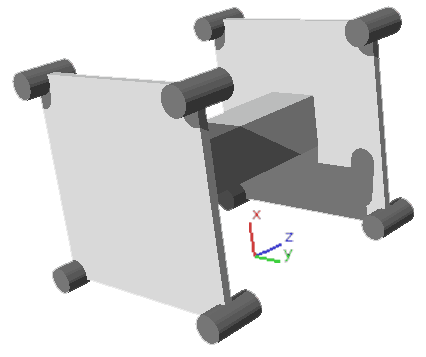 
For convenience of description, I’ve established a Cartesian coordinate system xyzw, where the w direction is vertical and can’t be shown in the top view, while the remaining xyz directions are the directions of the 3D ground. From our preparations, we know that the direction the 4D car can move should be the z-axis direction perpendicular to the side height (the cylinder base in the projection). This car has four front wheels and four rear wheels, connected by two square plates respectively, with an axle connecting the front and rear wheels in the middle. Whether to use plates or cross-shaped connections doesn’t really matter, as long as the eight wheels can be fixed. You might wonder: how do we explain the square plate’s corners being inserted into the cylinder? Actually, this is like the axle of a 3D wheel - in the top view, you see the axle inserted into a rectangle, while rotation occurs in the zw plane direction, with the remaining directions staying fixed, i.e., the 2D plane xy parallel to the side height, equivalent to an axle, which is exactly the position of the square. Of course, the axle must also be round, so what you see as a square thin plate in the top view is actually a cubinder with a very small diameter (its diameter equals the plate thickness, and the two perpendicular heights are the square’s side lengths).
The next problem: vehicles can’t always go straight - they need to be able to steer. Let’s first see how 3D cars turn: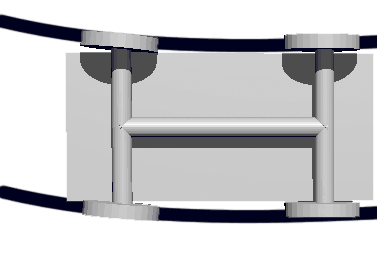 
The figure shows the turning paths of the wheels on both sides. The two front wheels guide, and the two rear wheels follow. Similarly for 4D cars, we only turn the four front wheels, leaving the four rear wheels fixed.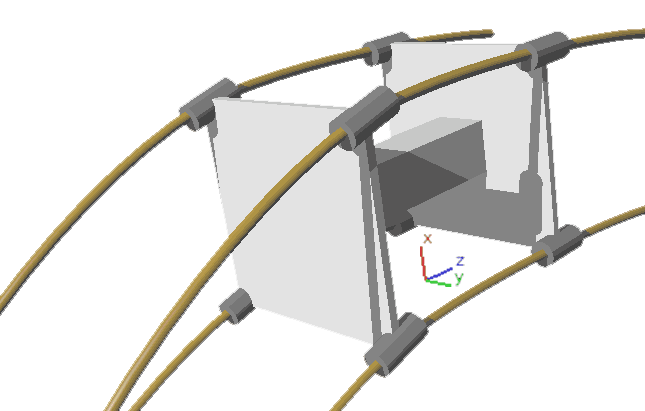
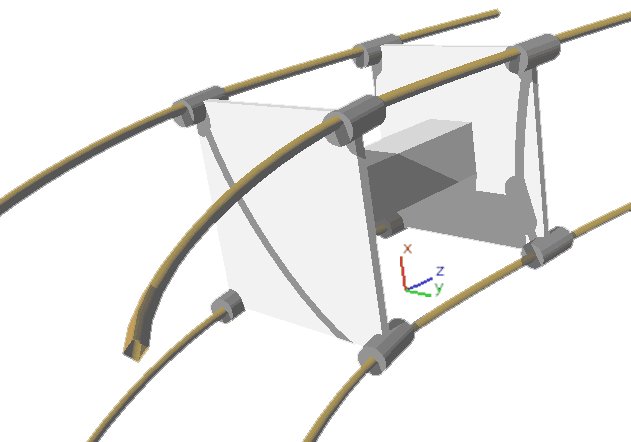
Other Types of Four-Dimensional Vehicles
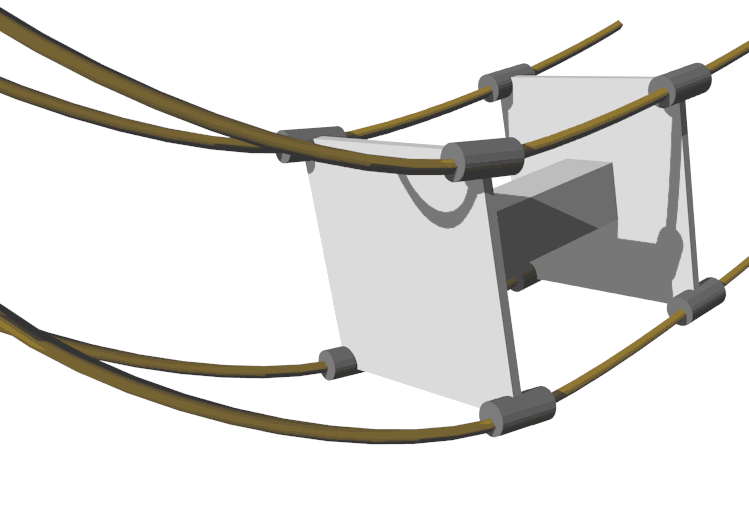
Actually, cars don’t have to turn only in x-axis or y-axis directions - they can turn in any direction on the ground perpendicular to the z-axis. This inspires us to actually build a “six-wheeled car” - with wheel vertices distributed at the vertices of a triangular prism. Its performance is almost the same as an eight-wheeled car, just that the eight-wheeled car is more stable. Of course, N-wheeled cars are all possible, and you can even design with N front wheels and M rear wheels in combination, or let N approach infinity - connecting all wheels together - this is also feasible, because these are all pattern variations in the shape of the side height direction that doesn’t participate in rotation, and don’t affect wheel rotation. The only downside is that steering might be too cumbersome - using this type of wheel for rear wheels is fine. These variations are like the trucks we see with many wheels side by side, either increasing stability or load-bearing capacity.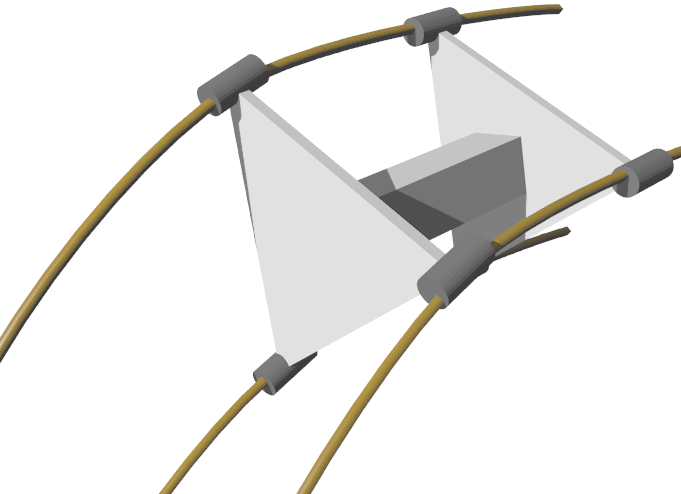 
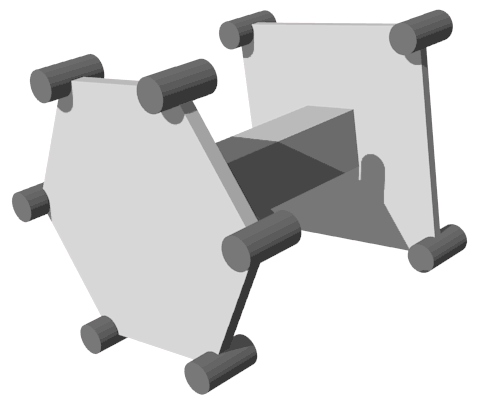
Are there other modes of movement? We know that 3D cars can only turn left or right because the ground is 2D, and planes only allow two rotation directions: clockwise and counterclockwise. So 4D car steering modes should correspond to all rotation directions in 3D space: for example, the two turning modes we saw earlier correspond to rotation around the x-axis and y-axis, so what mode corresponds to the remaining rotation around the z-axis? The z-axis is the forward direction, so this rotation is a kind of self-rotation, like a fighter jet rolling forward - the wheel tracks are helical. Can our previously designed car handle this type of steering? The answer is yes, though it’s not easy to imagine. I’ll leave this for readers to think about - the answer is at the end of the article. In summary, controlling a 4D car is similar to controlling a spaceship - you can freely soar in 3D ground space without gravity. If you want to drive yourself when touring the 4D world, you’ll probably need a pilot’s license to drive their cars.
Four-Dimensional Bicycles
As for bicycles, I think they can be divided into two-wheeled and three-wheeled types. Both are unstable when stationary and might fall over. But which is easier to control directionally, which has stronger stability, and other questions are beyond my cognitive abilities, so I won’t discuss them further here.
I haven’t drawn the pedal structure, as this part of the design is too difficult - it involves how 4D people’s legs grow…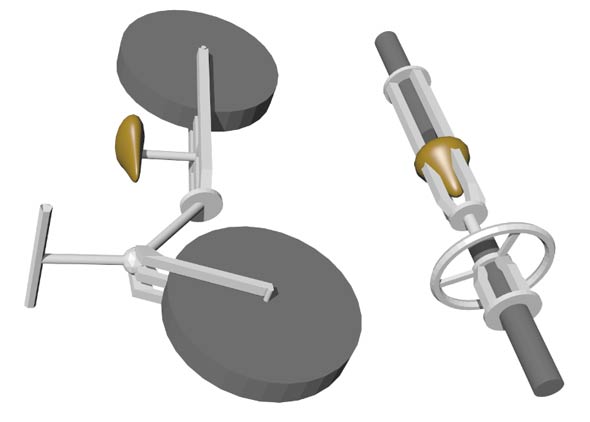
The 3D bicycle’s handlebars are just a one-dimensional stem, a simplified version of a steering wheel; similarly, 4D bicycle handlebars are also simplified, but they’re 2D, looking like our car’s steering wheel, but not really: when turning, you tilt it (as shown below), rather than turning the steering wheel around the axis in the middle of the side view. This might allow the bicycle to do self-rotating steering, but the friction is very large. I’m not clear whether it can actually be achieved - I’ll assume it can’t for now, because you must have a certain speed to turn the steering wheel for the car to possibly follow, and the car will stop self-rotating when the steering wheel is held in any position.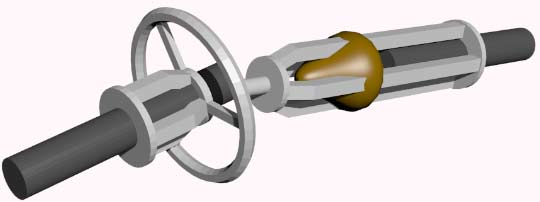
But a 3D tricycle placed directly in 4D space becomes a tricycle that can fall over: you can see the side view below as the top view of a tricycle lying on the ground.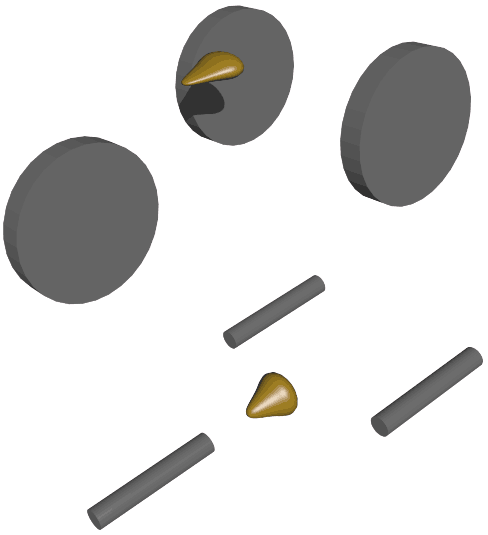
Speaking of this, the analogue of a stable 3D tricycle is obviously evident. Tricycles need three wheels because three points determine a plane, so the triangular configuration allows the vehicle to stand stably on the ground; the similar object in the 4D world is a four-wheeled vehicle, with wheels distributed on a tetrahedron. We still fix the rear wheels, leaving only one front wheel for steering. But the disadvantage of four-wheeled vehicles is that they might not be able to conveniently control self-rotation, for the same reason as bicycles. This is the vehicle with the minimum wheels required that won’t fall over in 4D space: if you forcibly overturn a four-wheeled vehicle, viewing the side view below as the top view of a tricycle lying on the ground, the middle rear wheel has height (perpendicular to the projection, not visible), so overturning requires effort to overcome gravity, just like when you overturn a tricycle in the 3D world.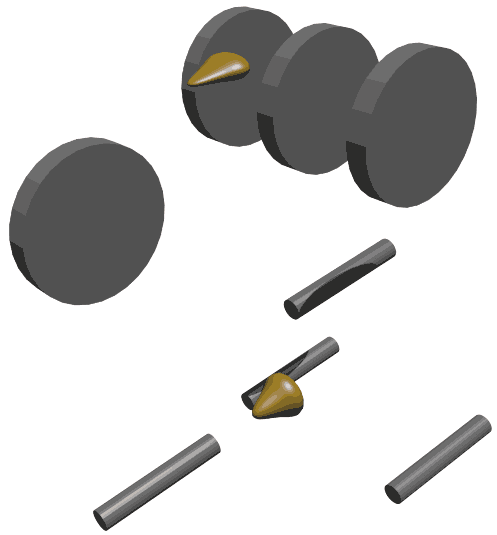
Car Steering System
Let’s discuss the design of car steering wheels: by analogy, car steering wheels should be spherical and can rotate around an axis. So the heavy transport vehicles in “The Wandering Earth” are four-dimensional! We’ve said that rotation in 4D space is around a plane as an axis (or the kind of double rotation where you can’t find a rotation axis), yet spheres have high symmetry - in 4D space they have a rotation axis perpendicular to the space they’re in. We can make a ball-cylindrical rod to transmit the steering wheel’s movement to the bottom.
Let’s first look at the simplest steering system of a 3D car: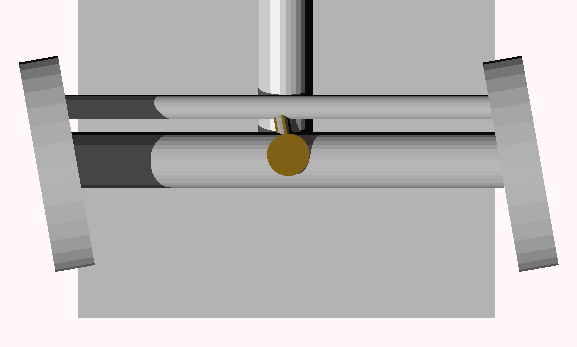
By analogy, we get the simplest steering system of a 4D car: (I’ve drawn the middle beam as semi-transparent for observation)
It’s similar to the 3D situation, but remember the self-rotation mode we left for you to think about earlier? You just need to self-rotate the steering wheel (rotate around the plane formed by the steering wheel’s vertical axis and the forward direction). Its characteristic is that each wheel faces a different direction, and each track is helical. This is how all possible steering of the car mentioned earlier corresponds to all possible rotations in 3D space. Two-wheeled and three-wheeled bicycles and four-wheeled vehicles might not be able to self-rotate well because their only front wheel can only be on the rotation axis. But note that it’s not the case that as long as there are two or more front wheels, they can do spiral motion (for example, the tracks of two wheels corresponding to the shape of DNA double helix structure). Self-rotation is different from general steering. When a 3D/4D car turns left, two/four front wheels tilt left, and the rear wheels maintain their direction, thus forming an angle difference between front and rear. But the spiral motion of self-rotation is achieved by the mutual angle difference of the four front wheels. The tracks of self-rotation are helical for both front and rear wheels, so if the rear wheels maintain their direction, it will cause the wheels to be twisted - if you really can’t understand this, imagine a left turn where only the left front wheel steers, but the right front wheel goes forward. So both front and rear wheels of 4D cars must be able to move, unless you give up the self-rotation steering function.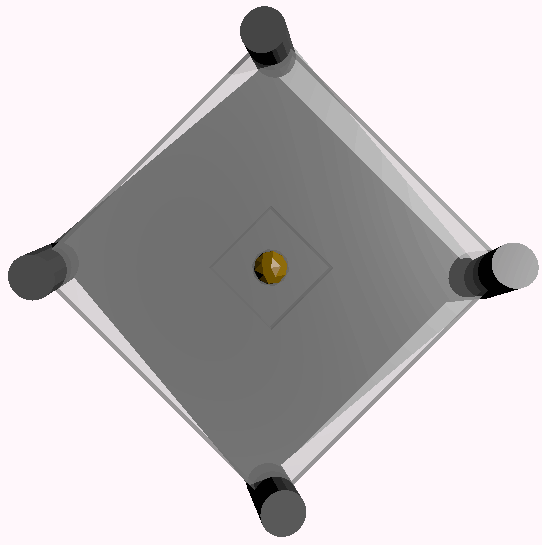
That’s all for road traffic vehicles in 4D space. If you have any new ideas or objections, feel free to discuss! Next, we’ll design lane divisions, road design, and rail transit systems on 4D roads.
Update
The 4D car simulator is now complete! The physics engine based on Newtonian mechanics can verify the above steering methods for cars. Can you drive the car out of the tunnel?
