4D Space (XV): Plane State Space (Part 2)
Rotations Acting on the State Space
We know that 2-vectors (bivectors) can generate rotations: for example, $\frac{\pi}4 e_{xy}$ represents a 45° rotation in the $xy$ plane from the positive $x$-axis towards the positive $y$-axis. Conversely, rotations can act on unit planes or 2-vectors, which indicates that a rotation transformation corresponds to a transformation within the plane state space. We define isoclinic rotations generated by self-dual 2-vectors as left-handed rotations, and those generated by anti-self-dual 2-vectors as right-handed rotations. Through geometric algebra, it can be proven that: when applying a rotation to a 2-vector, a left isoclinic rotation only acts on the self-dual component, and a right isoclinic rotation only acts on the anti-self-dual component.
Click here to expand/collapse the derivation
Since a simple 2-vector representing a plane is the sum of two equal-magnitude self-dual and anti-self-dual 2-vectors, a simple rotation is a combination of two left and right isoclinic rotations with the same rotation amount. For example, a 90-degree rotation around the $xy$ plane keeps the $xy$ and $zw$ planes invariant. Therefore, it can only be a rotation in the state space whose axes are the points corresponding to the $xy$ and $zw$ planes on the two spheres. We can verify this: this rotation maps the $yz$ plane to the $xz$ plane, and the $xw$ plane to the $yw$ plane, indicating that its state space indeed undergoes corresponding rotation transformations. 
When applying rotations to all plane spaces in four dimensions (i.e., S2XS2), if it’s an isoclinic double rotation, only one sphere rotates while the other remains stationary; if it’s a simple rotation, both spheres rotate with the same angular speed. For non-isoclinic rotations, both spheres will rotate, and their axes intersect the two spheres at four points, which represent the absolutely perpendicular rotation plane pairs. For a simple rotation, only one of the absolutely perpendicular rotation plane pairs is actually rotating, while the other is stationary. How do we distinguish them? The answer is by the direction of rotation: choose the pole on both sides that appears to rotate clockwise when viewed from the front; its corresponding plane’s Hodge dual is the rotation plane. These clockwise and counter-clockwise directions are not inherent; they depend on the orientation of the three axes of our self-dual/anti-self-dual space coordinate system. If we swap two axes, causing a change in space chirality, the conclusion will also be reversed.
Symmetry of the Hopf Fibration
By observing how rotations transform in the state space, we can also deduce some symmetry conclusions about the Hopf fibration. The planes containing the circles in a right-handed (or left-handed) Hopf fibration are actually the set of all planes that are right-handed (or left-handed) isoclinic with a certain plane; we call this a right-handed (or left-handed) isoclinic plane family. For a right-handed isoclinic plane family, it remains invariant under any left-handed isoclinic rotation, and such a rotation transforms planes within the family to other planes within the same family; it only remains invariant under a specific right-handed isoclinic rotation, which keeps all planes in the family fixed, meaning it can only rotate along the direction of the fibration’s circles. In other words, the orbital circles generated by right-handed isoclinic rotations are all right-handed isoclinic, and the orbital circles generated by left-handed isoclinic rotations are all left-handed isoclinic. Why are they the same? In fact, there is no deeper meaning; it’s merely a matter of definition: I intentionally choose the left-handed/right-handed relationship between planes to be consistent with the handedness of the trajectories of left-handed/right-handed rotations, and similarly, left-handed/right-handed rotations are intentionally chosen to correspond to rotations associated with left and right multiplication by quaternions. Swapping the definitions of left and right would be perfectly fine, only the conclusions would be reversed.
(Note: I found that my previous articles had inconsistent definitions of left-handed and right-handed rotations. I have taken this opportunity to unify the terminology in older articles.)
Angles Between Planes and Lines, Cells
In 4D, there are 2 more angle range problems:
- Given that the angles between planes A and B are $\alpha_1$ and $\alpha_2$, and the angle between plane A and cell C is $\beta$, find the range of the plane-cell angle $\gamma$ between B and C.
- Given that plane A and plane B have angles $\alpha$ and $\beta$ respectively with cell C, find the range of the two angles $\gamma_1$ and $\gamma_2$ between planes A and B.
We no longer focus on the angle range problem between a line and a plane in three-dimensional space, as it can be equivalently transformed into the problem of the angle between a line and the normal of the plane (their answers are complementary angles). The same applies to problems like the angle between a plane and a line, or a line and a cell, in 4D space.
To solve these problems, we must find a way to represent a cell or its normal vector in the plane state space (i.e., the two spheres). The normal vector of a cell is a unit vector in 4D space, and all such vectors form a hypersphere $\mathbb{S}^3$, which cannot be integrated into the two spherical spaces $\mathbb{S}^2\times \mathbb{S}^2$. Let us recall the formula for calculating the angle between a line and a plane: calculate the outer product of a unit vector and a unit 2-vector, obtaining a 3-vector whose magnitude is the sine of the angle. After some attempts, I found that the outer product calculation formula also cannot be directly expressed in the plane state space. Must we abandon dual decomposition and return to brute-force calculation with the most ordinary 6 coordinate plane bases? Later, I thought of an indirect method using the intersection line of planes to represent lines, which solved this problem.
Representation of Lines
If two planes have an intersection line, it means they are semi-parallel. All planes passing through a certain line should be pairwise semi-parallel, forming a semi-parallel plane family. Since two semi-parallel planes have equal distances on both spheres, I naturally thought: every correspondence between the self-dual and anti-self-dual spheres that preserves spherical distance gives a family of semi-parallel planes. This semi-parallel plane family should be the largest, because I have involved all points on both spheres, and there is no way to add points from other planes while still maintaining pairwise semi-parallelism. 
Each correspondence that preserves spherical distance is called an isometric isomorphism in mathematical terms. All isometric isomorphisms between spheres clearly correspond to the orthogonal group O(3), i.e., all rotations and reflection transformations on the sphere. Does this mean that every rotation and reflection transformation corresponds to a line through the origin in 4D space? Reflections, in particular, seem unnatural: rotation transformations are continuous, and the state space of 4D lines (a hypersphere) is also continuous, so reflection transformations are not needed, which indicates that this correspondence does not hold.
In fact, besides the case where all planes in a semi-parallel plane family are collinear (meaning they share a common intersection line), there is another possibility: they are all cocellular, in which case the family contains all planes within a three-dimensional cell. Although their intersection line is not unique, this determines the cell, and thus determines the normal vector. We see that the semi-parallel plane family is also not perfect; it exhibits two distinct modes: one is the collinear mode, and the other is the cocellular mode. 
The orthogonal group O(3) contains reflection transformations. We can divide the group into two parts (also called cosets) based on whether the transformation involves orientation reversal: the first part is pure rotations, and the second part is rotations with a single reflection. We hope that these two parts can correspond perfectly to the two types of semi-parallel plane familys. This is indeed the case: the family formed by the normal planes (i.e., absolutely perpendicular) to the collinear mode plane family is the cocellular mode, and absolute perpendicularity means keeping one sphere fixed and inverting the center of the other sphere to its antipodal point. Central inversion in three-dimensional space precisely changes its chirality (orientation), thus all clues are connected.
Which of pure rotations and rotations with reflection corresponds to the collinear mode, and which to the cocellular mode? This also depends on the choice of coordinate basis. Self-dual and anti-self-dual components are like two completely independent worlds; there is no special correspondence between them, and without a reference, it’s impossible to define whether the handedness (orientation) of the two spaces is consistent. If the coordinate basis is chosen as shown in the figure below, such a direct correspondence represents the x-axis.
Finally, there is a clever fact: the space obtained by identifying antipodal points on the three-dimensional sphere $\mathbb S ^3$ is the topological space composed of all rotations $SO(3)$ in three-dimensional space. The conventional proof uses the quaternion formula for representing three-dimensional rotations. Now we have another way to understand it: antipodal points on the three-dimensional sphere $\mathbb S ^3$ represent all lines through the origin in 4D space. Since we only need to choose one of the cocellular and collinear modes, we can fix an orientation and only consider rotation mappings, meaning each rotation uniquely corresponds to a line through the origin in 4D space.
Angle between a Plane and a Line
The next step is how to represent the angle between a line and a plane. Now a line is defined as an isometric isomorphism between the self-dual and anti-self-dual spheres. We naturally think that this mapping can pull the two components of a plane onto the same sphere to calculate distances. Does this spherical distance correspond to the line-plane angle? This is equivalent to pick out the plane from all planes parallel to that line that is isoclinic with the other plane (think about why). According to the definition of isoclinic planes, all lines on that plane form the same angle with the other plane, and this angle is clearly the desired line-plane angle. But note that the spherical distance is the sum or difference of the two angles, and its absolute value must be twice the line-plane angle. Therefore, the answer is that half of this spherical distance is the line-plane angle to be found. Using this principle, we finally have a tool that can precisely solve for the range of angles between all planes in a three-dimensional cell and another plane.
Solving Problem 1
Given that the angles between planes A and B are $\alpha_1$ and $\alpha_2$, and the angle between plane A and cell C is $\beta$, find the range of the plane-cell angle $\gamma$ between B and C.
Problem one can be briefly stated as: given the angles between two planes and the angle between one plane and a cell, find the range of the angle between the other plane and the cell.
The angles between planes in the state space are arc lengths on the sphere, while the angle with a cell is obtained by mapping points on the two spheres onto a single sphere to compare distances. Below, we fix the position of the cell (i.e., the mapping) and plane A (green point in the figure below). The possible range for plane B is represented by two circles on the two spheres (drawn as solid purple lines). The angle between plane B and cell C is the range of distances between points on the two circles after they are mapped onto the same plane. It is also known that the distance between the centers of the two circles after mapping is twice the given line-plane angle. The problem now becomes a spherical geometry problem: given the distance between two circle centers and their respective radii, find the minimum and maximum distances between points on the two circles. 
However, due to different specific angle values, the two circles may be separated, one may be contained within the other, or they may intersect. The final conclusion needs to be derived based on the specific situation. Given that circle 1 has radius $r_1$ and circle 2 has radius $r_2$, and the distance between their centers is $d$, I used AI to quickly summarize the range of distances between points on the two circles:
$$D \in [\max\left(0,\ d - r_1 - r_2,\ |r_1 - r_2| - d\right), d + r_1 + r_2]$$Substituting the specific angles:$$\begin{aligned}
d &= 2\beta \\
r_1 &= \alpha_1 - \alpha_2 \\
r_2 &= \alpha_1 + \alpha_2
\end{aligned}$$Remember that this spherical distance is actually twice the desired plane-cell angle. After simplification and rearrangement, we still need to divide by 2, yielding:$$D \in [\max\left(0,\ \beta - \alpha_1,\ |\alpha_2| - \beta\right), \beta + \alpha_1]$$This expression needs further correction: besides handling major arcs greater than 180°, we also need to handle cases greater than 90°. In 4D space, the figure formed by a line and a plane no longer has chirality even when orientation is considered. It seems we could use the right-hand rule, using our hand to indicate the direction of the plane’s vortex, and determining orientation by whether the thumb is in the same or opposite direction as the line. However, a human’s left and right hands in three-dimensional space can be flipped by a 4D transformation, thus losing their reference meaning. The situation with planes and three-dimensional cells is similar, as they are Hodge duals to the case of planes and lines. Therefore, we simply truncate and fold the part of the plane-cell angle range that is greater than 90°. Unlike handling major arcs greater than 180°, this is a true folding of the region, not just the boundary. Thus, when an endpoint of the interval hits the 90° boundary, it is truncated rather than “bouncing back.” Readers can experience and understand this in the simulator at the end of the article.
Solving Problem 2
Given that plane A and plane B have angles $\alpha$ and $\beta$ respectively with cell C, find the range of the two angles $\gamma_1$ and $\gamma_2$ between planes A and B.
Problem two can be briefly stated as: given the angles of two planes with the same cell, find the range of angles between the two planes.
Below, we fix the position of the cell (i.e., the mapping). Then, based on the cell mapping and the plane-cell angle, if we fix the positions of plane A and plane B on one sphere, their points on the other sphere form two circles. Let’s introduce the unknown $a=|\gamma_1-\gamma_2|$ representing the distance on the fixed-position sphere (taking values in $[0,\pi]$). We can use geometric relationships to find the range of distances between points on the two circles, which is the range of $b=|\gamma_1+\gamma_2|$. 
However, since there is an additional unknown parameter $a$, we need to perform case analysis for all possible situations where circles are separated, contained, or intersecting to comprehensively obtain the combined range of $a$ and $b$.
Online Simulator
Since case analysis is too cumbersome, we will directly examine the angle range using a random simulator, as we did last time.
Problem 1
Problem 2
Other Geometric Meanings in State Space
Re-interpreting Plane-Plane Angles
The two angle values $\theta_1$ and $\theta_2$ between two planes are defined as the maximum and minimum values of the angle between any line on one plane and the other plane. We can verify this in the state space: all lines on a given plane will have their corresponding mappings cause the points of that plane on the left and right spheres to align perfectly. This leaves one degree of freedom for rotation around that point, so the points of the other plane can form a complete circle with that point as the center, as shown in the figure below. 
The range of the angle $\alpha$ between a line and another plane can obviously be determined by the triangle inequality:$$\left| (\theta_1 - \theta_2) - (\theta_1 + \theta_2) \right| \leq 2\alpha \leq (\theta_1 - \theta_2) + (\theta_1 + \theta_2)$$Simplifying gives:$$\left|\theta_2\right| \leq \alpha \leq \theta_1$$If we ignore the handedness information indicated by the sign of $\theta_2$, this exactly matches the definition of the two angles between two planes.
Plane Spanned by Two Lines
We know that for the two mappings of a line, the points on both sides of the mapping represent planes passing through that line. Thus, the plane defined by two lines corresponds to source and image points that have the same value under the two mappings. Note that there are two pairs of such antipodal source and image points. We only need to choose one pair of points, because the other pair corresponds to the same plane, just with the opposite orientation of the 2-vector.
Thought Question of Last Article
If we select the vertices of regular polyhedra on each sphere in plane state space, and combine them pairwise to form all planes passing through the origin, what kind of symmetry do their intersection circles on the hypersphere exhibit? (There are a total of $5\times 5=25$ cases, excluding chiral isomers, there are 15 cases.)
Regular Octahedron - Regular Octahedron
First, let’s look at the case where both sides are vertices of regular octahedra.
Intersections and Number of Circles
Since a regular octahedron has opposite vertices, the same plane with different orientations will be counted twice. A regular octahedron has 6 vertices, so permuting and combining them yields $6\times 6=36$ 2-vectors. After removing duplicates, we get 18 planes. Will these 18 planes intersect? Since any two vertices on the left and right spheres can be arbitrarily moved along an edge by a fixed distance to find two other points, this implies that each circle will intersect at least some other circles. It is worth noting that there are two types of distances between vertices in a regular octahedron: the first is the distance between two points separated by one edge, and the second is the distance between two points at the farthest opposite positions. But the second type actually corresponds to the same plane with opposite orientation, so we don’t need to consider them here.
Number of Circles at Intersection Points
Given an intersection point, meaning a correspondence between any two vertices on the left and right spheres where each can move along an edge by a fixed distance to find two other corresponding points, the entire correspondence between the two spheres is determined: this is the intersection line of the planes, corresponding to the intersection point of two circles on the hypersphere. To find the number of circles at an intersection point, we need to find all planes consistent with this correspondence. The 6 corresponding vertices on each side of the regular octahedron represent 6 2-vectors. Again, excluding opposite directions, we get three circles intersecting at one point. Since the central angle between vertices in a regular octahedron is a right angle, according to the rule of semi-parallel plane angles in the state space mentioned last time, these three circles are also mutually perpendicular.
Total Number of Intersection Points
To find the total number of intersection points, we need to find all rotational symmetries of the regular octahedron (think about why). When choosing the first vertex correspondence, there are 6 possibilities. When choosing the second vertex, one can only rotate around that vertex as an axis, and the angle must be an integer multiple of 90°, so there are 4 remaining possibilities. Once two points are chosen, the entire rotation is determined, thus there are $6\times4=24$ different vertex correspondence mappings, corresponding to 24 lines through the origin in 4D space. However, these lines pass through the hypersphere twice, so the total number of intersection points is 48.
Number of Intersection Points on Each Circle
So far, it’s still hard for us to visualize this figure with 18 circles, 48 intersection points, and three mutually perpendicular circles intersecting at each intersection point. Therefore, let’s look at how many intersection points are on each circle. This requires knowledge about rotations. Once we find an intersection point on a circle, we can find other intersection points by rotating along the direction of the circle. As mentioned in the rotation section, a single rotation along the direction of a circle means rotating the same distance around its respective points on the left and right spheres in the state space. It is clear that to encounter other intersection points, the multiple of the rotation around a vertex of the regular octahedron must be an integer multiple of 90°, so we get 4 intersection points.
Specific Symmetry
A circle with 4 intersection points, and at each intersection point, three mutually perpendicular circles. Readers familiar with 4D regular polytopes will surely think of the 16-cell. However, besides these two conditions matching, other conditions are quite different: the 16-cell has 8 vertices and 24 edges. Dividing by 4 gives 6 circles. But our figure has as many as 48 intersection points and 18 circles.
Upon closer inspection, I found that although each circle in this figure only has 90° rotational symmetry, it actually has 8 intersection points. Our previous assumption that all intersection points were the same was incorrect (the adjacent two intersection points are orthogonally offset by 45°, so they cannot be connected by rotation). This figure can be seen as three 16-cells nested together at different angles.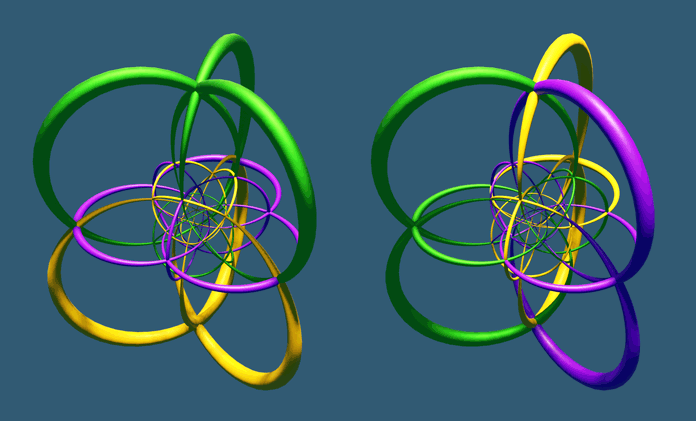
Cube - Cube
We can analyze this example as same as the regular octahedron. However, this example will have some differences.
Intersections and Number of Circles
A cube also has opposite vertices, which will count the same plane with different orientations twice. Permuting and combining yields $8\times 8=64$ 2-vectors. After removing duplicates, we get 32 planes. There are three types of distances between vertices in a cube: the first is the distance between two points separated by one edge, the second is the distance between two points separated by a face diagonal, and the third is the distance between two points separated by a body diagonal. The third type corresponds to the same plane with opposite orientation, so we ignore it. Thus, there are two types of distances, corresponding to two angles when circles intersect.
Number of Circles at Intersection Points
Once an intersection point is determined, the correspondence between the 8 vertices of the cube on both sides is determined. Again, excluding opposite directions, we get 4 circles intersecting at one point. According to the semi-parallel plane angle formula in the state space, the angles between these four circles are exactly equal to the spherical distances between vertices on the cube. This shows that the “vertex figure” formed by intersecting circles at an intersection point is a cube, meaning locally it looks like the intersection point is at the center of a cube, and other circles pass through the center to connect the cube’s vertices, forming that angular distribution. This explains why the intersection angles of the circles can have two types, similar to the distances between cube vertices.
Total Number of Intersection Points
To find the total number of intersection points, we need to find all rotational symmetries of the cube (think about why). When choosing the first vertex correspondence, there are 8 possibilities. When choosing the second vertex, there are 3 remaining possibilities (given that the vertices of a cube have three-fold symmetry). Once two points are chosen, the entire rotation is determined, thus there are $8\times3=24$ different vertex correspondence mappings, corresponding to 24 lines through the origin in 4D space. The total number of intersection points is still 48.
Number of Intersection Points on Each Circle
So far, it’s still hard for us to visualize this figure with 32 circles, 48 intersection points, and four circles intersecting at each intersection point arranged like cube vertices. Therefore, let’s look at how many intersection points are on each circle. Once an intersection point on a circle is found, we find other intersection points by rotating along the direction of the circle. To encounter other intersection points, the multiple of the rotation around a vertex of the cube must be an integer multiple of 120°, so we get 3 intersection points. But note that this rotation considers orientation; the planes at the other three intersection points have opposite orientations, and the angle directions are also opposite. The actual number of intersection points is 6.
Cocellular Circles
Two semi-parallel planes can define a three-dimensional cell. Correspondingly on the hypersphere, two intersecting great circles can define a great sphere. Earlier, we discussed the duality between cocellular and coplanar states: they are merely corresponding relationships where the left and right spheres are connected by a mirror reflection. Therefore, the total number of planes in the same three-dimensional cell is still the number of correspondences of vertices on a square (the property of cosets dictates that the number of reflections is equal to the number of pure rotations). After excluding opposite orientations, this means that on a hypersphere, there are 4 circles on a “great sphere equator.”
Great Sphere Equator
Let’s focus on the great sphere equator: it is composed of 4 circles, and each circle has 6 intersection points, which means that the circles must intersect pairwise. Readers familiar with three-dimensional polyhedra may have already recognized that this can only be the configuration of a cuboctahedron. Now we can finally intuitively understand why each circle seems to have 3 intersection points, but actually has 6: this figure inherently only has 120° rotational symmetry. In 4D Space (III): On Regular Polytopes, we pointed out that it appears in the central structure of the 24-cell. So, do all the circles in the entire figure form a 24-cell?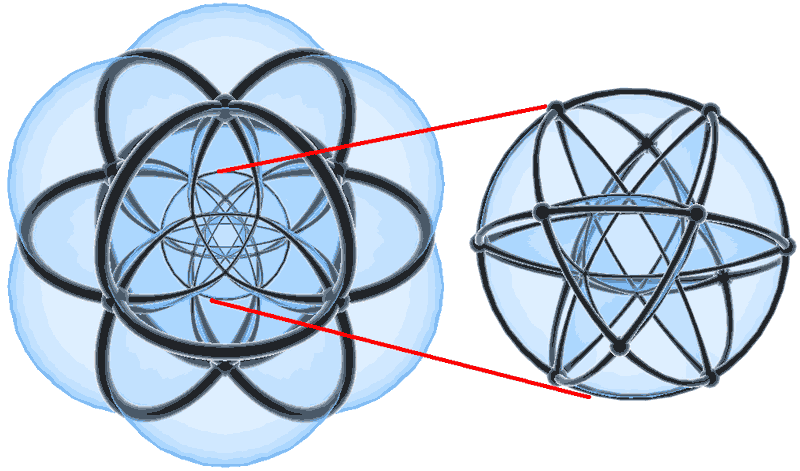 
Relationship with the 24-cell
The 24-cell has 24 vertices, 24 regular octahedron cells, 96 edges, and 96 triangular faces. When the 24-cell is projected onto a sphere, each great circle indeed has 6 intersection points, so the total number of circles is the number of edges divided by 6, which is 16 circles. Our figure has 48 vertices and 32 circles; these numbers are twice those of the 24-cell, so they clearly don’t match. However, the vertex figure of the 24-cell is indeed consistent with our figure, both being a cube. Therefore, locally, this figure strongly resembles the 24-cell, but the total number of primitives is doubled. To understand what exactly happened, we need to re-examine the vertices of the cube and the relationships of the associated rotational mappings. Previously, whether we used rotation or reflection to find cocellular or collinear planes, these were transformations that kept a certain vertex fixed. These transformations have a characteristic: if we color the vertices of the cube as shown below, we find that transformations that keep a certain vertex fixed will never rotate a vertex to a differently colored position. 
This indicates that all planes in our figure can be divided into two completely disjoint sets, and each set is a 24-cell! Finally, with the aid of a computer, we see that the spatial positions of these two sets of 24-cells are precisely dual to each other, reflecting the fascinating fact that the 24-cell is self-dual.
Regular Tetrahedron - Cube
The regular tetrahedron and the cube have a clever connection: a regular tetrahedron can be formed by alternately deleting half the vertices of a cube. In other words, by adding the antipodal points of the regular tetrahedron’s vertices on the sphere, a cube can be restored. Therefore, the regular tetrahedron - cube configuration differs from the cube - cube configuration only by half of the antipodal points, which represent opposite orientations of the same plane. Now, with the removal of duplicate orientations, this means that the regular tetrahedron - cube configuration is exactly the same as the cube - cube configuration, still generating two sets of mutually dual 24-cells.
Regular Tetrahedron - Regular Tetrahedron
Now we need to remove half of the vertices from the regular tetrahedron - cube configuration again. Since there are no longer any duplicated planes, this operation will delete all circles of half of the 24-cells, resulting in a pure 24-cell.
Regular Tetrahedron - Regular Octahedron
This figure indeed does not find equal length vertex distances on the two spheres. Therefore, the generated circles do not intersect pairwise. Since the regular tetrahedron is not a centrally symmetric figure, there are no planes with duplicated orientations (no double counting). A total of $4\times6=24$ circles are formed, which have no obvious special geometric meaning (if readers discover other important properties, please share).
Regular Dodecahedron - Regular Icosahedron
This figure also does not find equal length vertex distances on the two spheres. Therefore, the generated circles do not intersect pairwise. Since both figures are centrally symmetric, planes with duplicated orientations must be excluded. A total of $20\times12/2=120$ circles are formed, and they also have no obvious special geometric meaning.
Regular Icosahedron - Regular Icosahedron
The number of circles in the regular icosahedron - regular icosahedron combination is $12\times12/2=72$. This precisely generates a complete 600-cell: it has a total of 720 edges, which correspond to exactly 72 10-fold great circles on the hypersphere.
Regular Dodecahedron - Regular Dodecahedron
The number of circles in the regular dodecahedron - regular dodecahedron combination is $20\times20/2=200$. We hope it can generate a 120-cell. However, a 120-cell has four edges connected to each vertex, and its vertex figure is a regular tetrahedron, which lacks a complete circular structure. It can be proven that extending the edges of the 120-cell will yield this structure. Compared to the 120-cell, this structure also has additional intersection points at the original cell centers formed by the extended edges.
Now two types of vertex figure structures appear: one is the original 120-cell’s vertices, whose vertex figure is a regular tetrahedron, and after extending the edges, the vertex figure becomes a cube; the other is the additional intersection points at the original cell centers, whose vertex figure is a regular dodecahedron. These correspond to the length of an edge of the regular dodecahedron and the length of a diagonal of a regular pentagon, respectively. These diagonals can precisely form an inscribed cube, which explains the existence of two types of vertex figure structures. Further vertex distances will not yield new cases, because going to antipodal points will still result in one of these two cases.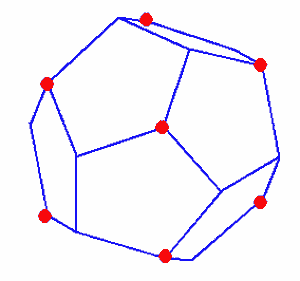 
Regular Dodecahedron - Cube
We see a very special relationship between the cube and the regular dodecahedron, which means that the regular dodecahedron - cube figure will have intersecting circles, and it can be seen as part of the figure generated by the regular dodecahedron - regular dodecahedron combination. This figure has chirality, and the vertex figures of the intersection points are all cubes. Interested readers are welcome to analyze its other properties. Here, we will just show the image.
Truncated Icosahedron - Truncated Icosahedron
Finally, let’s play with a big one: what kind of structure will two soccer-ball-shaped truncated icosahedra generate? I used a computer to generate $60\times60/2=1800$ circles, which was too slow and unclear to draw, so I didn’t bother to analyze it.