4D Space (XIV): Plane State Space (Part 1)
Introduction
Let’s first look at a simple angle range problem in 3D:
Given that the angle between vectors A and B is $\alpha$, and the angle between vectors B and C is $\beta$, find the range of the angle $\gamma$ between A and C.
This problem is simple using the geometric method: vector angles correspond to side lengths of spherical triangles on the unit sphere. Since the sum of two sides is greater than the third side, and the difference of two sides is less than the third side, with equality when collinear, the range of $\gamma$ is the closed interval $[|\alpha-\beta|,|\alpha+\beta|]$.
In 4D space, describing the relative position between two planes requires two angles, so the problem becomes:
Given that planes A and B have angles $\alpha_1$ and $\alpha_2$, and planes B and C have angles $\beta_1$ and $\beta_2$, find the range of the two angles $\gamma_1$ and $\gamma_2$ between planes A and C.
Unfortunately, we have no geometric intuition about angles between planes. Those planes that only intersect at a single point are already difficult to understand, making it hard to imagine how to solve this problem geometrically. Below, we will use the power of algebra to extract planes from 4D geometric space and place them in a state space with better geometric properties to solve the problem.
Definition of Plane State Space
Let’s consider a question: What kind of space is formed by the set of all planes passing through the origin in 4D space? Each point in this space represents a plane, and the space has dimension 4, which can be derived in multiple ways. (Click to expand/collapse derivation methods)
This is a curved, closed 4-dimensional space. How can we visualize it? A 2-vector has six components. If its magnitude is 1, then this space is at least on a 5-dimensional unit hypersphere in 6-dimensional space. However, when we combine with the simple 2-vector condition $af-be+cd=0$ (using letters $a$ through $f$ to represent the 6 components), we cannot see its specific shape at all.
Dual Decomposition
In “Four-Dimensional Space (7): N-Dimensional Vectors”, I introduced the dual decomposition of 2-vectors. Instead of using the usual 6 coordinate 2-vector bases $e_{xy}$, $e_{xz}$, $e_{xw}$, $e_{yz}$, $e_{yw}$, $e_{zw}$, we use 6 dual coordinate bases to represent planes. These bases can be divided into two groups. The first group consists of self-dual bases: $(e_{xy}+e_{zw})/\sqrt{2}$, $(e_{xz}-e_{yw})/\sqrt{2}$, $(e_{xw}+e_{yz})/\sqrt{2}$. The second group consists of anti-self-dual bases: $(e_{xy}-e_{zw})/\sqrt{2}$, $(e_{xz}+e_{yw})/\sqrt{2}$, $(e_{xw}-e_{yz})/\sqrt{2}$. This way, any 2-vector can be decomposed into self-dual and anti-self-dual parts, each containing three components. It’s easy to verify that the inner and outer products between these two parts are both 0. If we again use the Hodge dual to map the 4-vector $F\wedge G$ to a scalar, then for self-dual components, their inner and outer products are equal, while for anti-self-dual components, their inner and outer products are opposite. We denote the self-dual and anti-self-dual parts of a 2-vector $F$ as $F^+$ and $F^-$. The inner product of two 2-vectors is:
$$F\cdot G=(F^+ + F^-)\cdot (G^+ + G^-)=F^+\cdot G^+ + F^-\cdot G^-$$
Similarly, the outer product is:
$$F\wedge G=F^+\wedge G^+ + F^-\wedge G^-=(F^+\cdot G^+ - F^-\cdot G^-)e_{xyzw}$$
(Note: When we calculate the outer product of two 2-vectors later, we will default to taking the Hodge dual to eliminate the volume element $e_{xyzw}$ and keep only the coefficient in front, turning it into a scalar)
For a simple 2-vector $F$ that can represent a plane, its outer product with itself is zero, which means the magnitude of its self-dual component equals the magnitude of its anti-self-dual component: $F^+\cdot F^+=F^-\cdot F^-$. Since we’re interested in planes, their absolute size doesn’t matter. We can stipulate that both components have magnitude 1, so the three components of self-dual/anti-self-dual each correspond to spheres in two 3D spaces. The state space of all oriented planes is the direct product of these two spheres $\mathbb{S}^2\times\mathbb{S}^2$ (this can be viewed as the 4-dimensional edge of a double-sphere cylinder in 6-dimensional space). The direct product is the entire state space, where each point is an ordered pair formed by selecting one point from each of the left and right spheres. Why do we add the word oriented? Because $e_{xy}$ and $-e_{xy}$ are different points in $\mathbb{S}^2\times\mathbb{S}^2$, but they represent the same plane. Therefore, the true plane state space must quotient out the factor of $-1$. (Denoted as $(\mathbb{S}^2\times\mathbb{S}^2)/\mathbb{Z}_2$) Here are some examples:
We can see that if we simultaneously change the points on both spheres to their antipodal points, we get the same plane but with opposite orientation. If we only change the point on one sphere to its antipodal point, the new plane is absolutely perpendicular to the original plane.
Derivation of Angles Between Planes
The plane angle problem becomes clearer when transformed to this state space: We derived long ago how to find the angles between two planes F and G using inner and outer products, with the formulas:
$$\lvert \cos\theta_1\cos\theta_2\rvert={\lvert F\cdot G\rvert \over \lVert F \rVert \lVert G \rVert}$$
$$\lvert \sin\theta_1\sin\theta_2\rvert={\lvert F\wedge G\rvert\over \lVert F \rVert \lVert G \rVert}$$
The absolute values above are annoying. Actually, if we remove the absolute values and directly include all positive and negative signs in algebraic calculations, we can also deal with the direction of 2-vectors and plane chirality. Therefore, from now on, we neither want absolute values nor restrict the range of angle values. Also, if we assume that the magnitudes of the self-dual and anti-self-dual components of both planes are 1, then $\lVert F \rVert=\lVert G \rVert=\sqrt{2}$. Rewriting the inner and outer products between planes in terms of inner products of self-dual and anti-self-dual components, we get:
$$2\cos\theta_1\cos\theta_2=F^+\cdot G^+ + F^-\cdot G^-$$
$$2\sin\theta_1\sin\theta_2= F^+\cdot G^+ - F^-\cdot G^-$$
Adding and subtracting these two equations respectively, and using sum and difference angle formula of cosine function, we get:
$$\cos(\theta_1-\theta_2)=F^+\cdot G^+$$
$$\cos(\theta_1+\theta_2)=F^-\cdot G^-$$
We arrive at the most important geometric meaning in plane state space:
The angle between the self-dual components of two planes is the difference of the two angles between the planes, and the angle between the anti-self-dual components is the sum of the two angles between the planes.
Special Cases of Plane Angles
Here are some special positional relationships between planes:
- Coincident: $\theta_1=\theta_2=0$ (2-vectors have same direction) or $\theta_1=0$, $\theta_2=\pi$ (2-vectors have opposite directions).
- Left-handed isoclinic: $\theta_1=\theta_2=a$, characterized by $\theta_1+\theta_2=2a$, $\theta_1-\theta_2=0$.
- Right-handed isoclinic: $\theta_1=-\theta_2=a$, characterized by $\theta_1+\theta_2=0$, $\theta_1-\theta_2=2a$.
- Semi-parallel: $\theta_1>0$, $\theta_2=0$. Semi-parallel is characterized by $\theta_1+\theta_2=\theta_1-\theta_2$.
- Semi-perpendicular: $0<\theta_1<\pi/2$, $\theta_2=\pi/2$. Semi-perpendicular is characterized by $(\theta_1+\theta_2)+(\theta_1-\theta_2)=\pi/2$.
- Absolutely perpendicular: $\theta_1=\theta_2=\pi/2$.
In plane state space, these abstract angles are converted to two intuitive arc lengths on two spheres. Many previously seemingly mysterious conclusions can now be answered instantly. For example, same-chirality isoclinic plane relations have transitivity: same-chirality isoclinic planes mean their points on one sphere coincide, and coincidence between points is an equivalence relation, naturally having transitivity. However, different-chirality isoclinic planes don’t have transitivity. Observing the following figure makes both situations clear at a glance:
For another example, in “Four-Dimensional Space (4): Fibers and Hyperspheres”, we discussed the orthogonality of Hopf fiber bundles: I presented three Hopf fiber bundles with different orientations and pointed out that at every point on the hypersphere, three circles intersect orthogonally.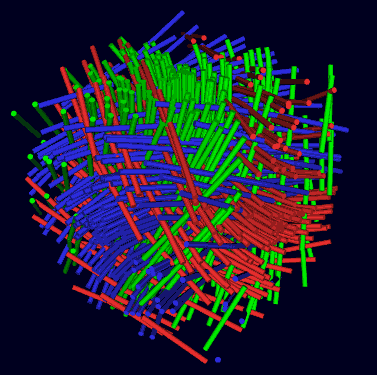
This conclusion can be further generalized: two same-chirality isoclinic plane families with different orientations intersect the hypersphere to obtain two families of fiber circles. The angles at which these two families of circles intersect on the hypersphere are all equal. We’ll prove this conclusion immediately: Without loss of generality, let’s assume both isoclinic plane families are left-isoclinic, then their anti-self-dual components can be chosen arbitrarily, while the self-dual components are two different fixed values. For two circles to intersect, their planes must be semi-parallel, which means their angles on the left and right spheres must be equal to the small angle between the circles. Obviously, the angle on the left sphere is fixed, so the angles between intersecting circles must all equal the angle value of the left self-dual components.
However, note that these angles are all algebraic values, allowing negative numbers or values larger than acute angles. Therefore, the above discussion is not rigorous enough to handle all plane angle range situations. Let’s first look at what it means when these angles take values outside acute angles.
Extending Angle Values
If we use the formulas relating inner and outer products without absolute values to angles as the definition of extended angles between two 2-vectors, we can obtain this diagram: (Actually first mentioned in 4D magnetic field force analysis)
Although the two angles can take any real numbers, due to the symmetry of $\theta_1$ and $\theta_2$’s roles and the periodicity of trigonometric functions, only the shaded region is the meaningful fundamental domain. Other regions represent plane positional relationships that duplicate situations in the fundamental domain. For example, when $\theta_2>\theta_1$, we can exchange the definitions of the two angles to reduce to the case where $\theta_1>\theta_2$, which is reflected in the figure as the extended region being symmetric about the diagonal line marked “left-isoclinic” where $\theta_1=\theta_2$. Similarly, for all diagonal lines marked isoclinic, there is reflection symmetry about them.
Note: If two 2-vectors’ inner and outer products have the same sign, they are defined as right-handed; if opposite signs, left-handed. It can be verified that this definition is independent of the choice of 2-vectors for the planes. Chirality is an intrinsic geometric property between planes.
This article mainly concerns the positional relationship between planes, i.e., ignoring the orientation information of 2-vectors but preserving the chirality information between planes: when $\theta_1>90°$, it means we can reverse one of the 2-vectors to make the angle acute again. On the diagram, this corresponds to rotating the right half of the rhombus 180° around the center to the left half. This includes treating coincident and oppositely coincident as the same point, treating self-dual and anti-self-dual as the same point, and also identifying points on the two right-isoclinic opposite edges and points on the two left-isoclinic opposite edges of the original rhombus. If we allow 4D creatures to flip them in higher-dimensional space so that left and right hands coincide without distinguishing chirality, then the fundamental space of the state space is reduced by half again, leaving only a right triangle.
Solving the Plane Angle Range Problem
Let’s look at the initial problem again:
Given that planes A and B have angles $\alpha_1$ and $\alpha_2$, and planes B and C have angles $\beta_1$ and $\beta_2$, find the range of the two angles $\gamma_1$ and $\gamma_2$ between planes A and C.
Adding and subtracting the original two angles, we get the angles on the two spheres in self-dual and anti-self-dual spaces. These two spaces are decoupled and don’t interfere with each other. Let the larger angle be numbered 1 and the smaller angle be 2. Then the sum and difference of both angles are positive and can form valid spherical triangles or collinear segment lengths, thus we obtain:
$$|(\alpha_1-\alpha_2)-(\beta_1-\beta_2)| \le \gamma_1-\gamma_2 \le (\alpha_1-\alpha_2)+(\beta_1-\beta_2)$$
$$|(\alpha_1+\alpha_2)-(\beta_1+\beta_2)| \le \gamma_1+\gamma_2 \le (\alpha_1+\alpha_2)+(\beta_1+\beta_2)$$
Drawing this range in the space of plane angles $\gamma_1$, $\gamma_2$, it’s obviously a rhombus region. However, we must also consider how to handle ranges that exceed the fundamental domain of plane angles (thick dark gray triangle)—using 180° rotation, the final answer only takes all yellow parts in the fundamental domain. If the range exceeds the large rhombus fundamental domain of 2-vectors, it seems that reflection about the isoclinic plane diagonal will definitely fall back into the original yellow region without adding new regions (hint: you can prove this starting from the maximum range of the sum of two angles), and can be directly discarded. However, this will cause some side of the spherical triangle to exceed $\pi$, but the distance between two points on unit sphere cannot be greater than $\pi$. In this case, we must select the minor arc on the other side to construct the spherical triangle, which ultimately manifests as: when angles exceed the rhombus region, instead of simply flipping the entire region, we only flip the boundary.
Note: We assume that the problem has already written the chirality information of the planes into the positive and negative signs of the corresponding angles. If chirality is indeed not specified, we can also substitute angle values for both chiralities and take the union of the two cases as the final result.
Here’s a specific numerical problem:
Planes A and B have angles 30° and 75°, planes B and C have angles 16° and 7°, and the chirality of planes A, B is opposite to that of planes B, C. Find the range of angles and chirality between planes A and C.
Based on the condition of opposite orientations, let:
$$\alpha_1=75°,\alpha_2=30°$$
$$\beta_1=16°,\beta_2=-7°$$
Then:
$$\alpha_1+\alpha_2=105°,\alpha_1-\alpha_2=45°$$
$$\beta_1+\beta_2=9°,\beta_1-\beta_2=23°$$
Since all angles don’t exceed 180°, we can directly use the spherical triangle range formula:
$$22°=45°-23° \le \gamma_1-\gamma_2 \le 45°+23°=68°$$
$$96°=105°-9° \le \gamma_1+\gamma_2 \le 105°+9°=114°$$
We obtain the equations of four boundary lines. Calculating their coordinates shows that most plane angles have the same chirality as the AB plane and opposite chirality to the BC plane, but within a small angle range, the angles have the same chirality as the BC plane and opposite chirality to the AB plane. You can try using the simulation program below to observe these two regions with opposite chirality.
Random Simulator
Here’s a small simulator I created using Monte Carlo sampling to verify the range of angles between two 2-vectors (i.e., oriented planes): First, I generate planes A and B with angles $\alpha_1$ and $\alpha_2$ using a fixed formula, then generate planes C and D with angles $\beta_1$ and $\beta_2$. Subsequently, we apply many random rotations to C and D simultaneously, and finally apply a rotation on C and D by using the LookAt algorithm from this article to align planes B and C. This way we obtain many samples that satisfy the angle constraints in the problem but have completely random orientations.
Operation instruction: Either input angle values or drag the corresponding points in the diagram to observe the distribution of yellow sample points.
A Challenging Problem
Let me leave you with a different and somewhat challenging problem, with the answer to be revealed in the next article: On each sphere, select only the 6 points passing through the coordinate axes. This gives 6×6=36 combinations from both sides, but since orientation is counted twice, there are only 18 different planes. Placing these planes at the origin and intersecting with the unit hypersphere gives 18 circles. What kind of symmetry does the figure formed by these circles have? Can it be viewed as the stereographic projection of some polytope? The points on the coordinate axes of each sphere actually form the vertices of a regular octahedron. If we select vertices of other regular polyhedra on each sphere and combine them pairwise to form all planes passing through the origin, what symmetry do their circles of intersection on the hypersphere have? (Including the octahedron just mentioned, there are $5\times 5=25$ cases in total, excluding chiral isomers leaves 15 cases)
To Be Continued
This article explored the transitivity of angles between planes. Later we will explore how to represent lines and cells in plane state space, and solve the problem of angle transitivity between planes and lines or cells. Interested readers can think about it first.









