4D Space (IX): Curved Shapes
Overview
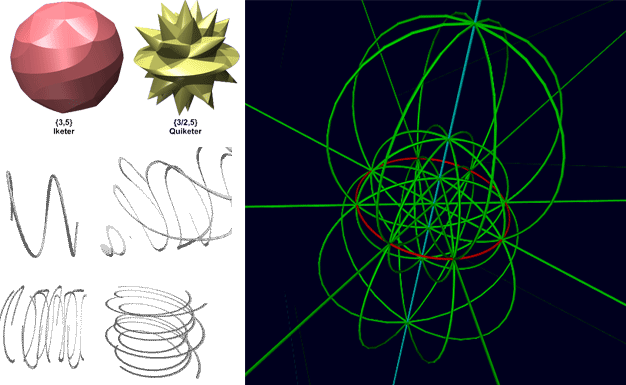
In this article, we will focus on curved surface (cell) shapes in four-dimensional space. We’ll first gain deeper understanding of some important solids of revolution from new perspectives (thickening, lofting) that were briefly introduced in the previous article More Geometries (with a list of common solids of revolution!). Then I will introduce some new geometric bodies: duocones, Polytwisters, and four-dimensional spirals.
<!-- Warning: Many images -->
Review: Flat Torus (or Clifford Torus)
The duocylinder is the direct product of two circles. It can be understood as a generalized cylinder with a circular base and circular lateral surface. What, you say a circular lateral surface is unimaginable? Let me tell you: a cylinder in three-dimensional space is actually a geometric body with a line segment as its base and a circle as its lateral surface.
The duocylinder is a closed four-dimensional figure with two congruent curved lateral cells, each lateral cell being the direct product of a solid circle and a hollow circle. The two three-dimensional lateral cells intersect at a two-dimensional curved surface, which is the direct product of two hollow circles. Here’s the key point: the key is to understand this two-dimensional curved surface in four-dimensional space - the duocylinder is simply its “solidification”.
According to the definition of direct product, the equation of that two-dimensional curved surface is:
$$
\begin{cases}x^2+y^2= r_1^2 \\ z^2+t^2= r_2^2\end{cases}
$$
We see that this two-dimensional curved surface can be placed exactly on a hypersphere centered at the origin with radius $\sqrt{r_1^2+r_2^2}$. Its stereographic projection is the torus from the last episode of Dimensions Mathematical Walk where longitude and latitude can be interchanged when flipped over! For this reason (and actually for topological reasons), we call this two-dimensional curved surface a flat torus. Let’s now focus on understanding this flat torus. How to understand it? Let’s describe the familiar cylinder using the same narrative approach we just used for the duocylinder: a cylinder is the direct product of a circle and a line segment. It can be understood as a generalized cylinder with a circular base and linear lateral surface, or with a linear base and circular lateral surface.
A cylinder is a closed three-dimensional figure with one curved lateral surface, which is the direct product of a line segment and a hollow circle. It also has “one lateral surface”, which is the direct product of the line segment boundary (two endpoints) and solid circles. Since the line segment boundary consists of two separated endpoints, this “one lateral surface” is actually two circles - what we usually call the two bases of a cylinder.
We see that because the lateral surface has gained one dimension, the duocylinder “connects” the two bases into one, thanks to the lateral surface being a closed circle without beginning or end. But why does the duocylinder, as a proper cylinder, project down to a holed torus? Actually, the same is true for cylinders! Note that we’re not projecting the duocylinder itself, but the intersection surface of the cylinder’s “two lateral cells”.
Similarly, the intersection of a cylinder’s curved lateral surface and another lateral surface (actually two separate circular figures) is the two circles at the top and bottom - this is the lower-dimensional analogy of the flat torus we’re looking for. It’s the direct product of a hollow circle and a hollow line segment (just two endpoints). This is a one-dimensional curve with equation:
$$
\begin{cases}x^2+y^2= r_1^2 \\ z= \pm h/2\end{cases}
$$
We see it naturally fits on a sphere, and its stereographic projection is either a large circle enclosing a small circle, or two separate small circles.
We finally understand: the holed torus is a product of projecting the lateral surface down, flattening it, plus projection magnification and distortion.
We’ve obtained a two-dimensional torus! We’ve successfully projected a perfectly good cylinder into a holed two-dimensional torus! It can be seen as generated by rotating a line segment around the origin in two-dimensional space, or by “lofting” a line segment along a circle - lofting refers to taking a given path and a cross-section (not necessarily two-dimensional), letting the cross-section move along the path to sweep out a shape, maintaining the cross-section perpendicular to the direction of movement during the motion (in three-dimensional space, this condition limits the cross-section dimension to less than three), so this movement is a combination of translation and rotation. Similarly, the holed torus is generated by “lofting” a circle along a circle - it’s the product of flattening the flat torus into three-dimensional space. Of course, a cylinder can also be seen as generated by “lofting” a line segment along a circle, just with different line segment orientations. The flat torus is also generated by “lofting” a circle along a circle, with the lofting cross-section and path being two absolutely perpendicular circles, while the holed torus surface corresponds to two circles that are half-perpendicular, half-parallel. We see that appropriately choosing the angle of the lofting cross-section can save one dimension.
Constructing the Torus
Let’s talk about the three-dimensional torus surface: a classic topological construction is to glue opposite edges of a square paper in the same direction to get a torus. In two steps: first roll it into a cylinder, second bend the cylinder over and glue the two ends together. But actually you’ve never successfully made a torus this way. You find that when bending an inelastic paper cylinder, the inner side gets compressed, so you can’t make a nice torus surface. But if we allow bending this cylinder in four-dimensional space, we can avoid this! We’ll get a perfect flat torus: this is also the origin of the word “flat” in flat torus - the Gaussian curvature is zero everywhere on the flat torus, and the paper won’t be compressed or stretched. This is like gluing the two ends of a rectangular paper strip together: in two-dimensional space you can only get a circle, and the paper strip must be compressed or stretched; in three-dimensional space it forms a cylinder lateral surface.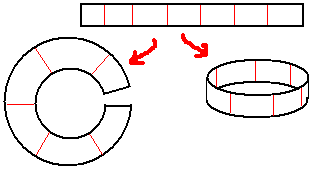
Imagine the direct product of a sphere and a circle: the sphere is in three-dimensional space, the circle is in two-dimensional space, and the direct product results in a three-dimensional curved body in five-dimensional space. Stereographic projection gives a spherical ring or toroidal sphere! The spherical ring can be thought of as bending a spherical cylinder over and gluing it together, but what about the toroidal sphere? It can be too! Just the specific method is a bit different. Actually there are two methods to glue a cylinder into a torus: the two resulting tori have their meridians and parallels exactly swapped!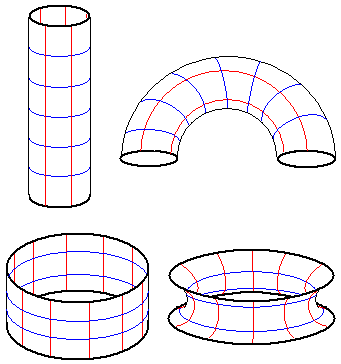
If you roll the hypersphere in five-dimensional space, you’ll see the spherical ring slowly turning inside out like swapping longitude and latitude to become a toroidal sphere. Actually the spherical ring, toroidal sphere, and the direct product of sphere and circle are topologically equivalent.
Finally let’s challenge the direct product of three circles: circles are in two-dimensional space, and the direct product results in a three-dimensional curved body in six-dimensional space. Using the similar lofting method to reduce dimensions, we can get figures in five-dimensional space, then reduce further to four-dimensional space to get two kinds of torus rings. They are both topologically equivalent to the object obtained by gluing the two ends of a torus cylinder (a cylinder with a torus as base cell) together, or by gluing opposite faces of a cube together in the same direction.
Thickened Bodies
Now we’ll understand many curved bodies from a completely new angle. We know that rope is one-dimensional and paper is two-dimensional, but strictly speaking these are all wrong because they have thickness. Let’s first look at what various low-dimensional figures become when they have certain thickness in three-dimensional space. First, surfaces: after giving a plane thickness, the surface becomes a board with thickness. Similarly, curved surfaces can also be thickened (like eggshells have tiny thickness): poke it with a line perpendicular to the curved surface. Due to thickness, the intersection is no longer a point but a line segment - this segment is the thickness. Then curves: poke it with lines perpendicular to the curve through each point; they will also detect thickness, meaning the cross-sections on the curve are all circles, adding thickness in both directions perpendicular to the curve’s tangent.
A circle in three-dimensional space thickened becomes a torus.
A torus is also a solid of revolution of a circle, and this circle’s size exactly reflects the thickness. When it shrinks to a point, the corresponding torus degenerates to a circle without thickness. This shows that “rotation” and “thickening” operations can be interchanged: a point thickened in two-dimensional space becomes a circle, and the figure generated by rotation equals a torus; we can also say a point’s rotation trajectory is a circle, and thickening the circle in three-dimensional space gives a torus.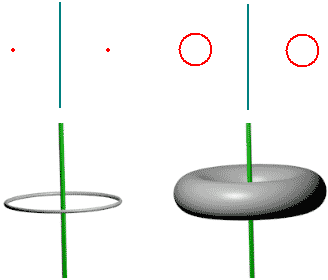
Another example: thickening a circle in two-dimensional space equals thickening the rotated sphere surface in three-dimensional space into a shell with thickness.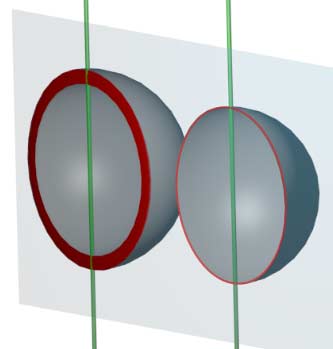
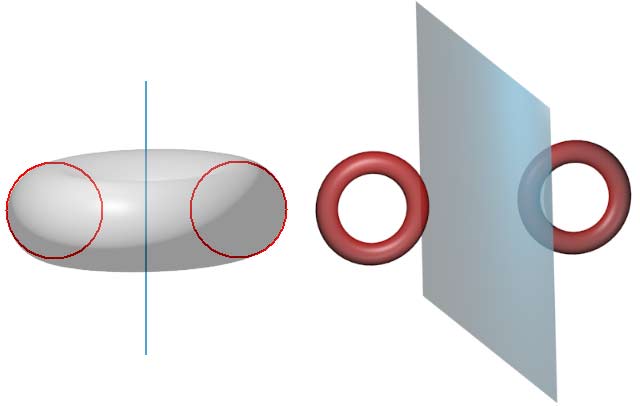
In four dimensions, a straight line thickened becomes a spherical cylinder, because thickness needs to be added in three directions, with spherical cross-cells; a circle thickened becomes a spherical ring; a plane thickened becomes the direct product of the plane and a circle reflecting the thickness size (adding in two directions) - if the board is rectangular it becomes a cylindrical prism; a sphere surface thickened becomes a toroidal sphere; finally, three-dimensional cell thickening is similar to planes in three-dimensional space, with thickening in only one direction, resulting in a kind of “board”.
The tool of “thickening” is extremely helpful for understanding various figures with tori. For example, the spherical ring is defined as a solid of revolution obtained by rotating a sphere around an external plane. Imagine letting the sphere’s radius approach zero, then the spherical ring approximates a point rotating around an external plane, resulting in a circle; the toroidal sphere is slightly more abstract. We initially saw its cross-section animation as suddenly appearing as a hollow sphere surface, getting thicker then thinner and disappearing. If the cross-section animation just suddenly showed a hollow sphere surface flashing and disappearing, this would be a sphere surface without thickness. From another perspective, as a solid of revolution, the toroidal sphere is obtained by rotating a torus surface around a plane containing its axis of symmetry. When the torus surface’s minor radius approaches zero, the torus surface approaches a circle, and rotating the circle around a plane containing its axis of symmetry gives a sphere. For solids of revolution of tori, we can also use these methods to understand them: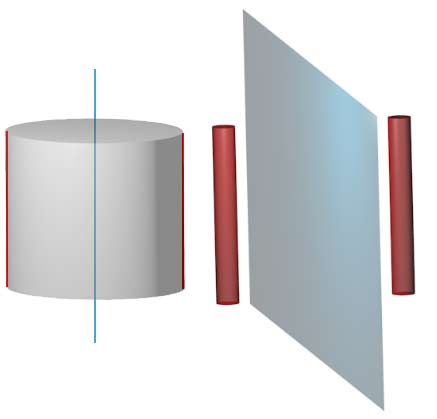
For example, this thickening effect of the double torus is very obvious: cutting the double torus at a 45° angle produces a “tiger cage” structure.

(The duocylinder oblique cut animation is from this website) It’s clearly visible that these cross-sections are thickened bodies of the edges (flat torus) of the duocylinder’s cross-cells (only approximate, as sections not perpendicular to the normal don’t capture uniform thickness). Finally, I want to remind that when saying a torus is a thickened body, it means thickening a circle in three-dimensional space into a solid torus; saying thickening a torus refers to thickening the surface of the solid torus we just mentioned - the torus surface, resulting in a double torus. Actually thickening the three-dimensional solid torus is also possible, resulting in a very thin torus cylinder. However, all flat three-dimensional figures thickened are simply cylindrification operations (height is the thickness), so there’s not much point in discussing them.
Higher-Dimensional Extension of Thickening and Lofting
For four-dimensional space, we analyzed that a straight line thickened becomes a spherical cylinder, and a curve thickened becomes what is actually a lofted body: a sphere lofted along a curve.
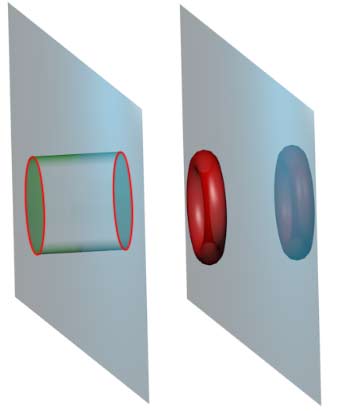
A plane thickened becomes a cylindrical prism. What about curved surfaces? Each point on a curved surface has a normal plane. When thickening, all directions on the normal plane gain uniform thickness, so the normal plane intersecting the thickened body gives a circle. We can think of the thickened body as a circle lofted along a two-dimensional curved surface: the circle moves along the two-dimensional curved surface while maintaining the circle perpendicular to the surface’s tangent plane. This direction is unique. If the cross-section isn’t circular (corresponding to non-uniform thickening), the cross-section can rotate during lofting. This phenomenon also exists in three-dimensional space, like some twisted prisms. Non-circular cross-section lofted bodies in four-dimensional space are even more abstract. I’ve temporarily thought of these two figures:
- Direct product of two two-dimensional tori: rectangle lofted on a flat torus;
- Cylinder with a thick spherical shell as base cell (thickened spherical cylinder lateral surface): rectangle lofted on a sphere surface;
- Cylinder with a thick toroidal shell as base cell (thickened torus cylinder lateral surface): rectangle lofted on a torus surface;
Finally, I want to summarize the relationship between direct product and lofting: direct product is a special kind of lofting where the path figure and cross-section figure’s spaces are absolutely perpendicular, so the cross-section figure only needs translation; general lofting has the path figure only perpendicular to the cross-section figure’s tangent space at one point, and translation to other positions requires adding rotation for correction. If there are no dimensional restrictions, we can always rotate the cross-section to a position absolutely perpendicular to the path, turning all lofting into direct products, so lofting and direct products are topologically completely equivalent (homeomorphic).
Double Cones
We know the cylinder’s analogies include spherical cylinder, cylindrical prism, and duocylinder; the cone’s analogies include sphone, cylindrone, and conical cone. Now we’ll see there also exists a duocone similar to the duocylinder!! I’ll give three ways to understand it.
As a Solid of Revolution
Rotating with the cone’s base as the rotation plane gives a highly symmetric figure - the duocone. First, the cone’s base circle remains fixed on the rotation plane, while the cone’s apex rotates one revolution to get a circle absolutely perpendicular to the cone’s base. These two circles actually have equal status (might not be very intuitive). Note these two circles are hollow structures, they are protruding edges on the duocone’s surface, and there are no two-dimensional solid circular surfaces on the duocone.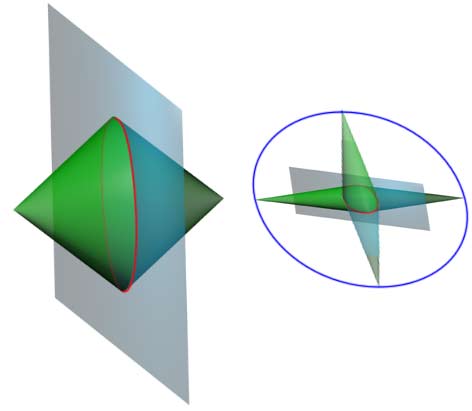
As a Bipyramid
To truly understand that the two circles have equal status, we need to first understand a new geometric body - the duopyramid. Its definition is: given two absolutely perpendicular planar figures $A$ and $B$ both centered at the origin, take their convex hull, denoted as $A+B$ (Schläfli symbol). What is a convex hull? Figuratively speaking, it’s like covering the figure with a layer of plastic wrap, wrapping it tightly. For example, a square is the convex hull of two mutually perpendicular line segments, an octahedron is the convex hull of three mutually perpendicular line segments, or the convex hull of a square and a perpendicular line segment. A duopyramid formed by placing two n-pyramids base to base is the convex hull of a regular polygon and a line segment. We note that its dual polyhedron is an n-prism.
Moving to four dimensions, the 16-cell is the convex hull of four mutually perpendicular line segments, or the convex hull of two absolutely perpendicular squares, or the convex hull of an octahedron and a perpendicular line segment… More generally, the convex hull of regular p and q polygons we call a p,q-duopyramid (p,q-duopyramid), and its dual polytope is a p,q-duoprism.
Inflating these onto the hypersphere and projecting down gives two circles at the north and south poles with p and q points respectively, and north-south running edges in between. Points on the two polygons are connected pairwise, each cell is a tetrahedral cell formed by combining edges from their respective polygons pairwise.
The duocylinder and duocone also inherit the duality relationship between duoprisms and duopyramids. The duocylinder has two congruent lateral cells, the duocone has two congruent circular edges. The duocylinder’s unique two-dimensional edge, the flat torus, corresponds to the duocone’s unique curved cell.
We know that cones in three-dimensional space can also roll, but not straight rolling - rather spinning around the apex. We’ll see later that the duocone’s rolling method is very special, because the two circles on the $xy$ plane and $zw$ plane simultaneously play the role of apex. Since rolling analysis is troublesome, I won’t expand on it here.
(Update: The rolling simulator based on 4D rigid body mechanics is ready, click here!)
Cross-section Animations
To be honest, I can’t imagine these cross-section animations at all:

List of Important Solids of Revolution
Let’s summarize various common four-dimensional solids of revolution: this table shows what three-dimensional figures they are and what plane they rotate around.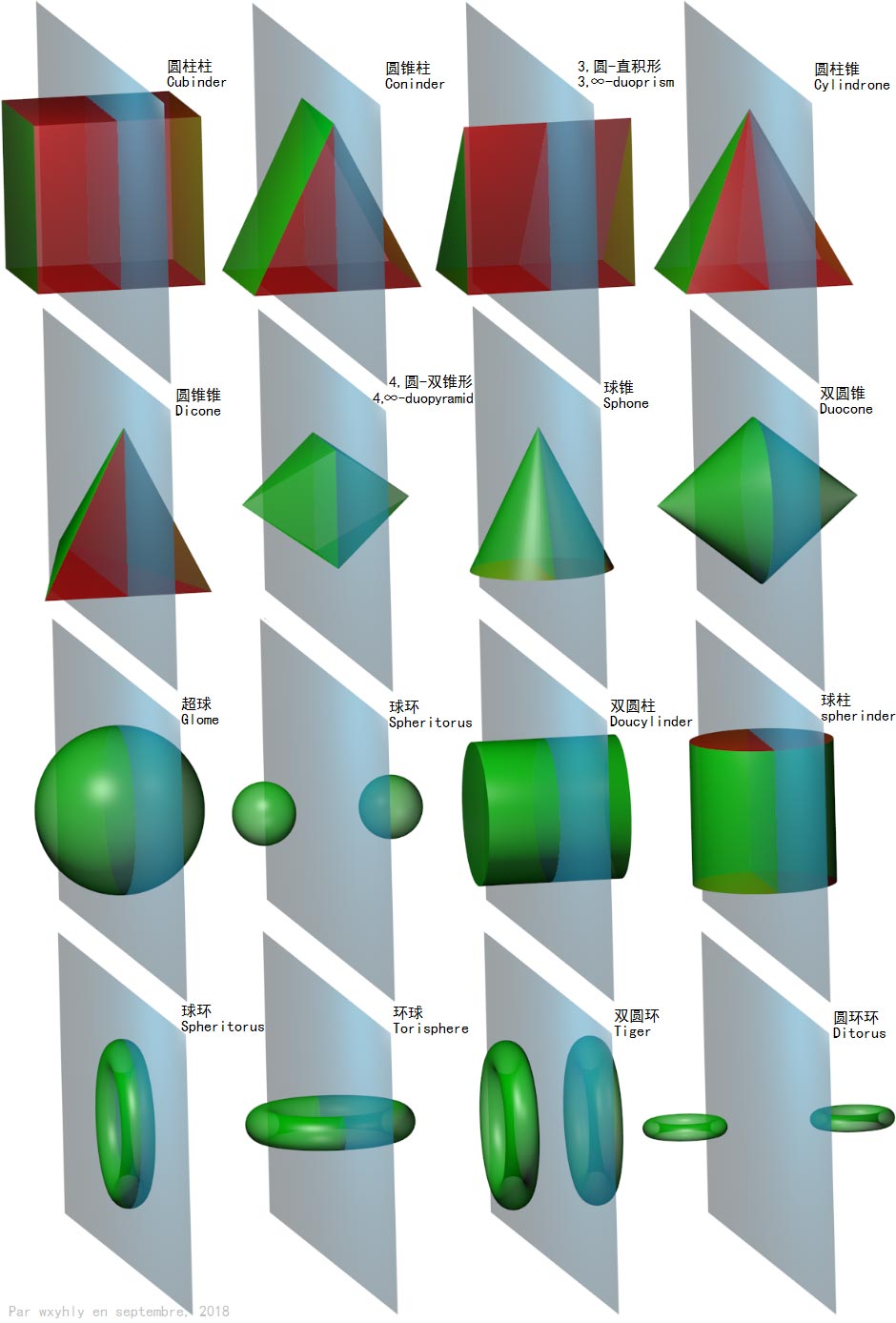
I’ve colored green the surface parts of three-dimensional figures that generate four-dimensional curved cells after rotation, and colored red the parts that generate flat three-dimensional cells after rotation.
Polytwister
We have another tool for creating geometric bodies - convex hull. Actually, the rhombic dodecahedron is the convex hull of a cube and an octahedron; the duocylinder is the convex hull of a flat torus. The duocylinder is the convex hull of two orthogonal circles. What if the circles are oblique? We’d probably get something like an oblique duopyramid, not very interesting. But we know that circles on the Hopf fibration all make equal angles with each other. Each circle $z_2=k z_1$ can correspond to a point on an abstract sphere through the complex number $k$. If we inflate a regular polyhedron framework onto this sphere, then the Hopf circles corresponding to points on these frameworks will maintain a highly symmetric structure with the original regular polyhedron’s symmetry. Taking the convex hull of all these circles will give us something called a Polytwister. I learned about Polytwisters from this website. (Update in 2025: Later I discovered that there are two definitions of Polytwister. One is the convex hull described above, which results in softer edges. The other is the intersection of many bicylinders, producing sharper edges. What is actually shown below are all hard polytwisters.)
Under stereographic projection, Hopf circles are linked together, so when we take the convex hull we get some bands twisted once around. For example, below is the Polytwister corresponding to a regular dodecahedron.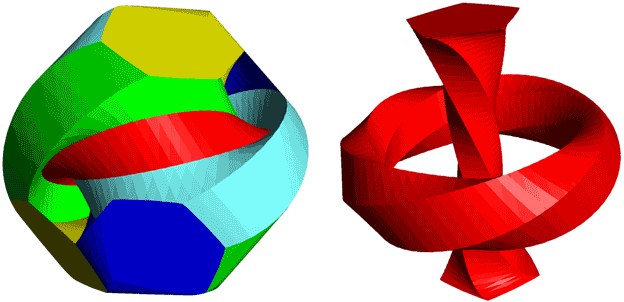
Cutting open these twisted bands gives us the Polytwister’s net:
It’s worth mentioning that when taking the convex hull, those hollow pentagons are flattened at the edges on those skeletons. When placing the Polytwister on the ground, the tangent parts are these pentagons. Its lateral surface is somewhat similar to a duocylinder - it can roll in one direction while having edges in other directions. Its local structure is like the direct product of a pentagon and a circle, but the whole is twisted once around! As for whether this thing will rotate in the twisting direction when rolling forward, I don’t know.
Both images above are from the website just mentioned, which also has images of Polytwisters corresponding to other regular polyhedra, semi-regular polyhedra, and even star polyhedra! All this is thanks to the “ingenious craftsmanship” of Hopf fibration. Polytwisters can be seen as partially discretized Hopf fibrations. Completely discretized examples include the 600-cell, which is the result of further discretizing the Polytwister corresponding to the regular icosahedron (replacing twelve Hopf circles with decagons then taking the convex hull, resulting in the 600-cell’s 120 vertices):
Four-Dimensional Spiral Surface
A three-dimensional helix is the trajectory of a point doing circular motion while simultaneously translating in the perpendicular direction. In four dimensions, we might analogize this as a circle rotating while translating in the perpendicular direction, sweeping out a two-dimensional curved surface. Then its cross-section animation along the translation direction would be a rotating circle. Note that the region it sweeps is a sphere surface, inside which a solid sphere can fit. Translating over time becomes a spherical cylinder, meaning this “spring” can fit over a spherical cylinder.
Below are cross-section animations from various directions:
Its parallel projection has severe self-intersection, looking like a helical surface:
Are there other possible shapes? Like a square rotating while translating? (Note, the rotation here is restricted to the three-dimensional space perpendicular to the translation direction, and to get a four-dimensional figure, the square can’t rotate in its own plane) This “square spring” can fit over a cylindrical prism! Actually there are even crazier constructions: what do you get when a helix rotates while translating? A helix can rotate in two different directions. I can’t imagine these things anymore, but that doesn’t stop us from drawing their cross-section animations: The first type rotates around a direction perpendicular to the helix translation direction - I have to say it’s too strange.
The other type rotates around the helix translation direction, but due to the helix’s properties it can be considered as not rotating, instead equivalent to the helix translating up and down, finally resulting in a kind of oblique helical cylindrical surface.
Finally, you might also ask, why should the analogy of a helix be a 2-dimensional curved surface, why not continue to be a one-dimensional curve in four-dimensional space? It’s indeed possible, but I haven’t found any line-like things that look particularly like helices yet…
Previous View Series Contents Next