Mercator Projection

The first episode of “Dimensions: A Walk Through Mathematics” talks about using stereographic projection to create maps. But we both know that the world maps we are familiar with are not made this way. Stereographic projection is only used to map the polar regions. World maps use another type of projection, and the map it produces is not infinitely large, but a rectangle. This projection is called the Mercator projection, and like stereographic projection, it is conformal.

The general idea behind the Mercator projection is to take a cylinder whose axis coincides with the Earth’s axis of rotation, project points from the sphere onto the lateral surface of the cylinder, and then unroll the cylinder to get a rectangular map. But the specific method is not as simple as keeping the z-axis constant and mapping to the cylinder, nor is it a direct projection from a light source at the center of the sphere. To maintain conformality, we can calculate a special function called the Gudermannian function. The North Pole, however, would be projected to infinity, making the map finite in width but infinite in length (since the cylinder is infinitely long). The world maps we see are finite rectangles because the areas near the poles are cut off.

Why do we choose the cylinder’s axis to coincide exactly with the Earth’s axis of rotation? What if we chose an arbitrary angle? We would get world maps you’ve never seen before!So I found a relatively high-resolution rectangular world map online, used the inverse Mercator transform to get 3D coordinates, rotated the sphere, and then used the Mercator projection again to get a world map we have never seen before. The map I found was not a strict Mercator projection (you can see it’s not conformal near the poles), so I could only make some attempts. At first, I thought that projecting points from the sphere onto the cylinder’s lateral surface meant keeping the z-coordinate constant, but with this method, the image I got had a lot of distortion at the North and South poles. Another idea was that the projected z-coordinate had a linear relationship with the latitude, which is to apply a sine transform to the original z-coordinate. Only then did the image look relatively normal. During my debugging, I even had an unexpected discovery: (I have no idea how I got this anymore)
It reminded me of Liu Cixin’s science fiction novel “The Earth’s Cannon,” which tells the story of building a tunnel through the Earth to create a high-speed passage.
Back to the main topic, below is the image from Wikipedia showing a cylinder with an axis parallel to the equatorial plane:

Click here to see the map viewer with Mercator projection at any angle

Let’s do something even more interesting: project polyhedra with Mercator projection! Now I’ll place a regular dodecahedron on a sphere. We’re familiar with the stereographic projection shown in the second episode of “Dimensions.” But what if we try the Mercator projection? The projection results are as follows:

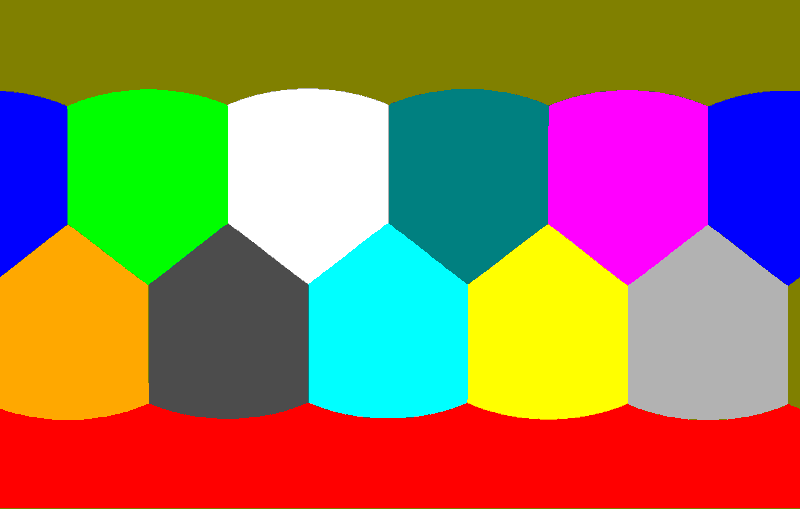
Click here to see the online demo of Mercator and stereographic projections of a regular polyhedron with an arbitrary pole

For this demo, I used an inverse algorithm: I iterate through every pixel on the screen, use the inverse Mercator transform to get its 3D coordinates, and then determine which face it belongs to in order to color the pixel differently. The specific method is to consider the pixel to belong to the face whose center it is closest to. So, to draw polyhedron A, I need the vertex data of its dual polyhedron (i.e., the face center data of polyhedron A). The advantage of this approach is that I don’t have to worry about tedious problems like the order of vertices or how the edges are connected; it’s simple and brute-force.

Here are the Mercator and stereographic projections of a soccer ball I made as a bonus (^-^):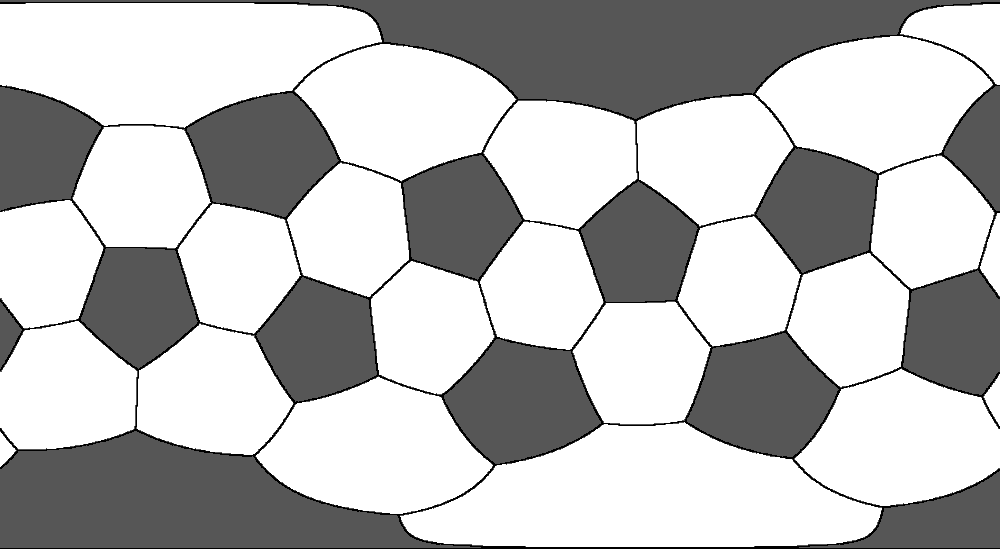

Pour aller plus loin: La Dimension 4

Can the Mercator projection be analogized to four-dimensional space? First, we need a projection from a sphere to a cylinder. In four dimensions, we have a projection from a hypersphere to a spherinder, but the lateral surface of a spherinder (the Cartesian product of a sphere and a line segment) cannot be unrolled. We could use the Mercator projection a second time to unroll the spherinder’s lateral surface into a hyperrectangle. But this secondary projection feels strange. Another approach is to project directly onto a cubinder and then unroll it into a hyperrectangle, but a cubinder is the Cartesian product of a square and a circle, which doesn’t feel right. It would be better if we could project onto a duocylinder (the Cartesian product of a circle and a circle) and unroll it. But what is the lateral surface of a duocylinder? A duocylinder is bounded by two congruent curved cells. These curved cells are the Cartesian product of a solid circle and a circle. They can be unrolled into a cylinder (by straightening the circle). This would mean we need two separate cylinders to construct the world map, which also feels strange… I haven’t yet thought of a perfect solution to this problem. Welcome everyone to give better idea.