Featured Content
- Solids of revolution, lofted solids
- Julia-Mandelbrot transition animation
- All four-dimensional analogues of quadric surfaces
Table of Contents:
- Solids of Revolution
- Lofted Solids
- Four-Dimensional Fractals
- Quadric Hypersurfaces
- Answers to Thought Questions
Solids of Revolution
In the previous article, we saw direct product shapes like the duocylinder and some analogues of tori. They were filled with many “circular” things, and circles generally come from rotation. Let’s look at those familiar and unfamiliar geometric shapes in four-dimensional space from the perspective of solids of revolution.
Cylindrical Prism as a Solid of Revolution
Everyone knows that a rectangle rotated around one edge produces a cylinder, so what can produce a cylindrical prism by rotation? Let’s analyze a cylinder: its base is a circle, which of course comes from a line segment rotating around an endpoint, while the cylinder “stretches” the line segment into a rectangle and “stretches” the rotation point into a rotation axis. So the cylindrical prism is an upgraded rectangle, “stretched” into a rectangular box, rotating around a face.
What if the face is slightly farther away?
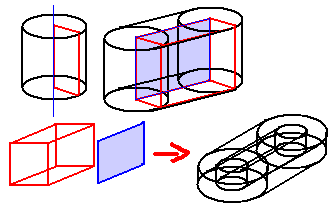
If we translate the rotation face slightly so it’s at a certain distance from the rectangular box, we’ll get a “toroidal cylindrical prism” (the direct product of a torus and a rectangle). The torus here is the 2D kind with two concentric circles. When the inner radius of the torus is 0, it becomes the previous case: cylindrical prism (direct product of circle and rectangle).
Rotating Cylinders and Spheres
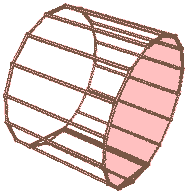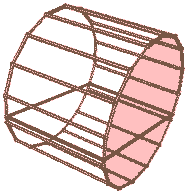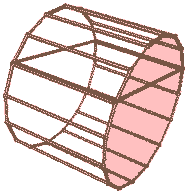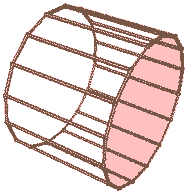
Think about this: what geometric shapes do we get when rotating cylinders and spheres in four-dimensional space? Since cylinders aren’t highly symmetric, we can choose different rotation planes: the base, a plane through the axis of symmetry, a plane parallel to the base at some distance from the cylinder, a plane parallel to the axis at some distance from the cylinder, etc., yielding different shapes. (We could also choose any oblique plane, but the irregular shapes obtained have little significance.) Let’s look at a cylinder rotating around its base: Since rotation in four-dimensional space is very abstract and we cannot directly visualize the rotation process, we can only “reduce dimensions” using the “cross-section animation” method. How exactly do we reduce dimensions? Pretending we don’t have the ability to directly visualize 3D circular solids of revolution (i.e., tori), we can do this:
 |  |
Here’s the case of a cylinder rotating around its base:
|
|
|
Look, the cross-section animation on the right shows that this geometric shape is a duocylinder! Other cases of choosing rotation planes are left for you to think about; I’ll publish the answers at the end of the article.
A sphere rotating around a plane outside it produces a spheritorus, which is the most primitive definition of a spheritorus, while a sphere rotating around a plane through its center produces a hypersphere (think about the case of a circle and it’s not hard to understand). Why not let the sphere rotate around a plane that doesn’t pass through the center but intersects the sphere? Because this shape is self-intersecting (again think about the circle case - that thing looks like an apple), and I don’t consider self-intersecting shapes to be well-formed.
Rotating Tori
I have four relatively “proper” (not oblique) choices for rotation planes: two types that don’t intersect the torus itself were discussed last time, and there are two more special position planes:
- A plane through the axis of symmetry: We also mentioned that rotation produces a spheritorus.
- The symmetry plane of the torus perpendicular to the axis: Left as a thought question, answer at the end of the article. (Hint: You can start by imagining cross-section animations)
Cylindrical Cone, Conical Cylinder, Conical Cone as Solids of Revolution
Actually, with the cylindrical prism, we’ve already discovered a pattern: when “stretching” a solid of revolution to higher dimensions through “prism” operations, its rotation “unit” is also “prismified”, and the same goes for cones. So a cylindrical cone comes from rotating a quadrilateral pyramid around a triangular side face, with this side face perpendicular to the blue rectangular base. (When discussing 3D shapes, perpendicular means dihedral perpendicular; don’t forget that four-dimensional space also has absolute perpendicularity)
Similarly, a conical cylinder is formed by rotating a triangular prism (blue triangle “prismified”), and a conical cone is formed by rotating a triangular pyramid (blue triangle “conified”). (Red indicates rotation plane in the figure below)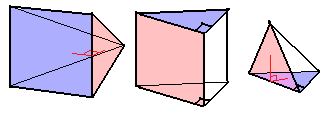
Return to Contents
Lofted Solids
I’ve used 3D software like 3ds Max before, which has a modeling method called “lofting”: taking a 2D shape object as a cross-section along a certain path to form complex 3D objects.
For example, a cylinder can be seen as its base lofted along a straight line, and a torus can be seen as a circular cross-section lofted along another circle. Four-dimensional space certainly has lofting too: when we loft a 3D cross-section along a straight line, we get a 4D prism; along a circle, we get a solid of revolution; along other curves, we can get more complex 4D objects. But unlike 3D, 4D also has “2D lofting”: we loft a 2D cross-section along a 2D surface! If the 2D surface is flat, it corresponds to a direct product; if curved, it becomes complex. We’ve only seen one type of rotational torus - the spheritorus - which is a circular cross-section lofted along a spherical surface. If 4D civilizations have something like 4D modeling software, this would surely be a great modeling method.
I imagine the pipes and roads used by 4D civilizations are probably lofted solids.
Four-Dimensional Fractals
Mandelbrot-Julia Sets
After watching Episode 6 of “Dimensions” - Fractals, the only thing it gave me was awe. We now want to unify those two magical sets - the Julia set and the Mandelbrot set - in four-dimensional space.
The definition of the Julia set is: given a number $z$ on the complex plane, you continuously perform the operation: $z\to z^2+c$ (where $c$ is a fixed complex number), and eventually your $z$ will likely calculate to infinity. All those initial $z$ values that don’t go to infinity form the Julia set on the complex plane. Of course, the shape of the Julia set varies with the complex number $c$. Imagine if you take $c$ to be something like 10000 - whatever $z$ you pick will definitely get larger and larger when squared, i.e., go to infinity, so the Julia set for $c=10000$ is the empty set. The set of all $c$ values for which the Julia set is not empty forms the Mandelbrot set. (Quite convoluted)
There’s a theorem that guarantees: if a Julia set is divergent at $z=0$, then it must be empty, so the Mandelbrot set can also be defined as: the set of $c$ values for which the iteration $z\to z^2+c$ starting from $z=0$ doesn’t diverge.
$z$ is a complex number, and $c$ is also a complex number, so we can get a complex number pair $(z_0,c)$. Definition: if starting from $z=z_0$ and performing the iteration $z\to z^2+c$ doesn’t diverge, then the complex number pair $(z_0,c)$ belongs to set $P$. Note that this complex number pair actually describes four-dimensional space $(x,y,z,w)=(Re (z_0),Im (z_0),Re (c),Im (c))$, so our Julia set can be seen as the shape obtained by intersecting set $P$ in four-dimensional space with the plane $z=Re(c),w=Im (c)$, and the Mandelbrot set is the shape obtained by intersecting set $P$ with the plane $x=0,y=0$. We call set $P$ the Mandelbrot-Julia set (unofficial name).
The Mandelbrot-Julia set is highly irregular, and we cannot directly visualize it (stereographic projection is impossible), so let’s look at its cross-sections with the 6 coordinate planes:
$xy$ plane: | $xz$ plane: |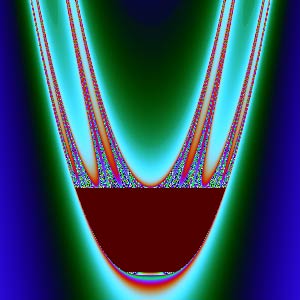
$xw$ plane: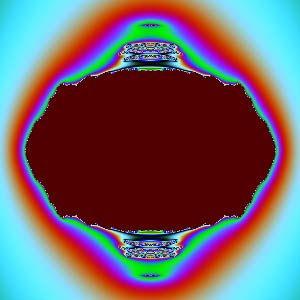 | $yz$ plane: |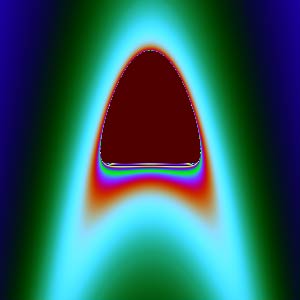
$yw$ plane: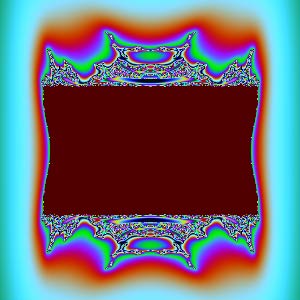 | $zw$ plane: |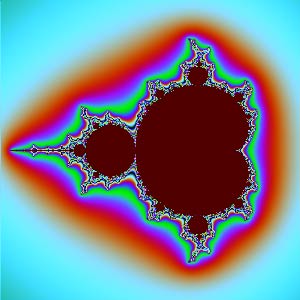
Except for the $xy$ and $zw$ cross-sections, why do the other cross-sections look so “ugly”? When zoomed in, they don’t show more delicate patterns, appearing to be “torn” into irregular filaments. The secret to complex transformations producing beautiful patterns is: they are all conformal (angle-preserving) transformations. Conformality ensures that tiny shapes maintain their form and won’t have “filamentous tearing”. The $xy$ plane happens to be the real and imaginary parts of complex number $z$, and that circle is the Julia set when $c=0$. The $zw$ plane happens to be the real and imaginary parts of complex number $c$, corresponding to the Mandelbrot set. But $xz$, $xw$, $yz$, $yw$ are combinations of components between two complex numbers. Once we split complex numbers apart like this, they lose their internal connection, conformality is lost, and the images become ugly.
We now rotate the $zw$ plane containing the Mandelbrot set to the plane containing the Julia set, and the cross-section can slowly transition from the Mandelbrot set to the Julia set! But don’t forget that the Julia set passing through the origin is just a circle ($c=0$), so we also need to add a translation transformation. To prevent “filamentous tearing” during rotation, we must choose planes that give complex numbers $z$ and $c$ equal status - planes at equal angles to both the $xy$ plane and $zw$ plane! As mentioned in the previous introduction to fiber bundles, the set of equiangular planes (same chirality) corresponds one-to-one with circles in the fiber bundle, and thus with points $k$ on a sphere (where $z=k c$). If we place the Mandelbrot set plane at the south pole, then the Julia set absolutely perpendicular to it is at the north pole. The transition animation needs to choose a path from south pole to north pole, but there are infinitely many - all meridians connect the two poles. Choosing different meridians gives us different transition animations. I’ve chosen the prime meridian here (actually the position of 0 longitude isn’t fixed):
Others
Direct visualization of 4D fractals is almost impossible, but we can still imagine some fractals that 4D beings would enjoy. 
For example, the famous Cantor ternary set’s 2D generalization isn’t very interesting to planar beings: they can’t see those hollow squares inside, they might prefer an analogue like the one on the right:
 |  |
But for us 3D beings, the one on the right is almost “crumbled to bits”, while the Sierpinski carpet in the middle looks more pleasing.
3D space corresponds to three types of analogues: one that also looks almost “crumbled to bits” to us - the “Menger-Sierpinski snowflake”, the classic Menger sponge, and another that 4D space beings would like: hollowing out a cube, hollowing it out again and again. But we can’t see inside the cube, just like 2D beings can’t appreciate the Sierpinski carpet.
This type of 4D fractal analogue should be divided into 4 types: crumbled to bits, riddled with holes like the Menger sponge, with many 3D holes dug out (these holes are connected in 4D space), and hollow hypercube cavities that even 4D beings cannot appreciate.
A nice-looking 3D analogue of the Mandelbrot set is the Mandelbulb. In 4D we could use quaternions (4D analogue of complex numbers) to create fractals, but conformality likely can’t be maintained, so we might have to use 4D polar coordinates (algorithm: forcibly square the distance coordinate, double the angle coordinates) and abandon quaternions. But regardless, I believe Mandelbulb4D should look even better,
Return to Contents
Quadric Hypersurfaces
Everyone should know about quadric surfaces: paraboloids, cylinders, spheres, hyperboloids, cones, saddle surfaces, etc. They’re called “quadric surfaces” because their equations are quadratic. In 3D space, these are ternary quadratic equations; in 4D, they’re quaternary quadratic equations. Since this involves equations, it’s obviously an algebraic problem, so I’ll try to give more intuitive conclusions about quadric hypersurfaces rather than derivations.
There are so many quadric surfaces in 3D space - how are they classified? This involves the problem of standard quadratic forms. We won’t discuss this in detail, but here’s the classification method:
We can always establish a coordinate system such that most surfaces have equations of the form $ax^2+by^2+cz^2=d$ in that coordinate system.
Regardless of which coordinate system we find, the equation has the same number of positive and negative terms, so we can classify surfaces (hypersurfaces) using this criterion. So for 3D space we have:
| Number of positive terms | Number of negative terms | Sign of constant $d$ | Name |
|---|---|---|---|
| 3 | 0 | + | Sphere |
| 3 | 0 | 0 | A point |
| 3 | 0 | - | No solution |
| 2 | 1 | + | Hyperboloid of one sheet |
| 2 | 1 | 0 | Cone |
| 2 | 1 | - | Hyperboloid of two sheets |
Note that cases with fewer positive than negative terms are duplicates of the above - they become the same after negating both sides of the equation. We only list cases with equal coefficients here; ellipsoids, elliptic paraboloids, etc. are just scaling transformations of the above cases and are omitted here.
But we seem to have missed some surfaces: their equations have one term that isn’t quadratic - either missing entirely (cylinders: circular cylinder, parabolic cylinder, hyperbolic cylinder) or linear (paraboloid, saddle surface).
Following this line of thinking, let’s look at quadric hypersurfaces in 4D space:
| Number of positive terms | Number of negative terms | Sign of constant $d$ | Name |
|---|---|---|---|
| 4 | 0 | + | Hypersphere |
| 4 | 0 | 0 | A point |
| 4 | 0 | - | No solution |
| 3 | 1 | + | Hyperboloid of one sheet |
| 3 | 1 | 0 | Spherical cone (light cone) |
| 3 | 1 | - | Hyperboloid of two sheets |
| 2 | 2 | + | “Direct product” hyperboloid |
| 2 | 2 | 0 | “Direct product” double cone |
Their equations have one term that isn’t quadratic: either missing entirely (cylinders: we won’t list them here, all 3D quadric surfaces can be “stretched” into cylinders) or linear. Let’s focus on linear terms: when a linear term appears, the constant term can be eliminated by translation, and there won’t be two linear terms appearing simultaneously - choosing an appropriate coordinate system leaves only one. So our table is simple:
| Number of positive terms | Number of negative terms | Name |
|---|---|---|
| 3 | 0 | Rotational paraboloid |
| 2 | 1 | Saddle hypersurface |
Let’s specifically introduce the unfamiliar shapes:
The hypersphere is a special case of the four-axis elliptic hypersphere (similar to sphere vs. three-axis ellipsoid)
Hyperboloid of one sheet (similar to hyperboloid of one sheet in 3D) has an axis of symmetry. Note that 4D space generally only has planes of symmetry (similar to 3D axes of symmetry), the axis of symmetry here is equivalent to spherical symmetry (similar to 3D point symmetry). Cross-sections of the hyperboloid of one sheet perpendicular to the axis of symmetry are all spheres.
Hyperboloid of two sheets (similar to hyperboloid of one sheet in 3D) also has an axis of symmetry, its cross-sections perpendicular to the axis are also spheres, but note it consists of two independent hypersurface parts, like the hyperboloid of two sheets - when the cross-section is between the two “sheets”, nothing is intersected.
Spherical cone: It’s also an axially symmetric (spherically symmetric) figure. Its cross-section animation perpendicular to the axis is a sphere uniformly shrinking to a point then uniformly expanding. The light cone in relativity is a spherical cone! (The uniformly expanding sphere corresponds to the expansion of the observable universe, with the sphere’s volume being the Hubble volume) Our theme is space, not spacetime, so we won’t expand on this.
“Direct product” double cone: This figure is somewhat abstract, but manageable. Look at its standard equation: $x^2+y^2=z^2+w^2$. Does it feel familiar? If I set $x^2+y^2=z^2+w^2=1$, this is the equation of the intersection of two hypersurfaces of a duocylinder. That is, the “direct product” double cone intersects with a hypersphere, and the intersection projected down is that toroidal surface! It’s highly symmetric: it has symmetry planes $xy$, $zw$, and actually all planes at equal angles to $xy$, $zw$ are symmetry planes. But cross-section animations can’t give us more information.
“Direct product” hyperboloid: This figure is more abstract, but the “direct product” double cone is definitely the “asymptotic 3D surface” of the “direct product” hyperboloid (when the constant of the direct product hyperboloid approaches 0, we get the “asymptotic 3D surface” - think of the asymptotes of a hyperbola and the asymptotic cone of a hyperboloid). But cross-section animations also can’t give us more information. Welcome suggestions for better visualization methods.
Rotational paraboloid: Also an axially symmetric (spherically symmetric) figure, can be seen as a solid of revolution obtained by rotating a paraboloid around its plane of symmetry.
Saddle hypersurface: Equation: $x^2+y^2-z^2=w$. It’s a function: a 3D coordinate $(x,y,z)$ corresponds to a number $w$. A saddle surface is concave (convex) in one direction and convex (concave) in another, but 4D space doesn’t have such nice symmetry: it’s concave (convex) in one direction and convex (concave) in two other directions (on one plane). But this description is still quite abstract. Welcome suggestions for better visualization methods. CFY here shows several quadric hypersurfaces using the cross-section method.
Answers to Thought Questions
A plane through the cylinder’s axis of symmetry as the rotation plane produces a spherical cylinder.
A plane parallel to the base at some distance from the cylinder as the rotation plane produces the direct product of a 2D torus and a circle.
A plane parallel to the axis at some distance from the cylinder as the rotation plane produces a toroidal cylinder (direct product of a 3D torus and a 1D line segment).
The symmetry plane of the torus perpendicular to the axis as the rotation plane produces a spheritorus.