Geometry and Motions in p-Norm Space

//Note: This article was significantly revised in August 2020 and includes a lot of new content!
//Note: The last section on gravitational orbit calculations was corrected and supplemented in January 2023!

A Different Distance Formula

We all know the Pythagorean theorem states that the sum of the squares of the two sides of a right triangle equals the square of the third side. This is an indisputable fact, and there are various ways to prove it. The most famous is probably the “proof without words”: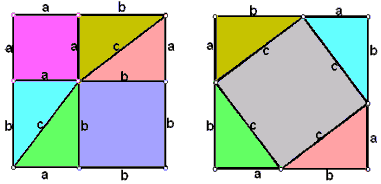

However, there is an issue with this proof because the Pythagorean theorem can be invalid! You’ve probably heard of non-Euclidean geometry. I mentioned a type of “hyperbolic geometry” in a previous article. Non-Euclidean geometry was originally a series of new geometries developed by negating the parallel postulate, but their essence lies in a different metric, meaning a different formula for calculating distance. The familiar formula for calculating the distance between two points, $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$, also comes from the Pythagorean theorem. If we “forcibly” define the distance as $d=\sqrt[p]{|x_2-x_1|^p+|y_2-y_1|^p}$, where the Pythagorean theorem becomes the sum of the p-th powers of the two sides equals the p-th power of the hypotenuse—we call this space a p-norm space. There’s an excellent short sci-fi story called “Pythagoras,” which tells the tale of a world where a wormhole causes the exponent in the Pythagorean theorem to deviate from 2 to 2.013. Although general relativity has proven that the exponent in the Pythagorean theorem for curved spacetime is still 2, this does not detract from it being a wonderful, imaginative story. What would it be like if such a space really existed? Let’s explore the fascinating p-norm space below.

First, the “circle” changes. The definition of a circle is the set of points in a plane equidistant from a fixed point. When the distance definition changes, the shape changes, and so does pi (the ratio of circumference to diameter) (of course, the “circumference” here must be calculated using the newly defined distance formula). Perhaps the most recent famous example is Xiaomi’s new logo design—its outer curve is a circle in 3-norm, and this single design cost 2 million yuan. Most introductions to p-norm space probably stop here. What would a world with p not equal to 2 (e.g., p=3) be like? The great expert Matrix67’s article discusses the geometry of the world where p=1, touching on problems like perpendicular bisectors and circumcircles. But why did our world choose the number p=2?

Speaking of circles, we must discuss the concept of rotation. In our world, the most perfect shape is the circle. But now we can’t say that with certainty. In a 3-norm (p=3) world, the curve $|x|^3+|y|^3=1$ is the “most perfect shape” because the trajectory of a moving point rotating around the origin in the 3-norm world is exactly the curve $|x|^3+|y|^3=1$. Thus, creatures in a 3-norm world would see this shape as identical from all directions (when rotating). This explanation sounds reasonable and seems to suggest we must adapt to this view and not put 2-norm space in a special position, but we will see that 2-norm space indeed has some special properties.

In our world, rotation can be represented by a matrix. For example, a point (x,y) rotating counterclockwise by an angle $\theta$ around the origin to point (x’,y’):$$\begin{pmatrix} x’ \\y’\end{pmatrix}=\begin{pmatrix}\cos\theta & \sin\theta \\-\sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}=\begin{pmatrix}x \cos\theta+y \sin\theta \\-x \sin\theta+y \cos\theta\end{pmatrix}$$What would a rotation transformation look like in p-norm? Before studying p-norm geometry, let’s look at another famous geometry: Minkowski space.

Minkowski Space

What happens if we define the distance formula as $d^2=(x_2-x_1)^2-(y_2-y_1)^2$? First, the circles in this world become hyperbolas, and the circumference of a hyperbola is infinitely long! (Calculated using a line integral.) The value of pi in this world is positive infinity, and rotation has no period! The strangeness doesn’t stop there; the weirdest thing is that sometimes the length becomes an imaginary number! This is because the value under the square root might be negative when calculating distance.

It’s hard to believe such a strange space exists, but it is spacetime! The distance expression in four-dimensional spacetime is $d^2=x^2+y^2+z^2-t^2$.
If $x^2+y^2+z^2-t^2>0$, the distance here is a spatial interval, which we call “spacelike”; if it’s less than zero, we take the absolute value and then the square root to get a time interval, which we call “timelike”; and if the value under the square root is exactly 0, we call it “lightlike.” Minkowski’s four-dimensional spacetime is an excellent mathematical model for relativity. For example, the famous Lorentz transformation can be written like our familiar rotation matrix:
$$\begin{pmatrix} x’ \\t’\end{pmatrix}=\begin{pmatrix}\cosh\theta & -\sinh\theta \\-\sinh\theta & \cosh\theta\end{pmatrix}\begin{pmatrix}x \\t\end{pmatrix}$$
In fact, the Lorentz transformation is a rotation in four-dimensional Minkowski space! Furthermore, this transformation does not change the nature of a vector (avoiding paradoxes like going back in time to kill your grandparents), meaning it transforms a spacelike (timelike, lightlike) vector into a spacelike (timelike, lightlike) vector. It also explains why we can only infinitely approach the speed of light (acceleration is rotation, and rotation has no periodicity).

Generalized Trigonometric Functions

For hyperbolic functions, we have $\cosh^2\theta-\sinh^2\theta=1$. Similarly, we can assume that in p-norm, there are trigonometric functions $\sin_p$ and $\cos_p$ that satisfy $\sin_p^p\theta+\cos_p^p\theta=1$. For hyperbolic functions, $\theta$ is the “hyperbolic angle”—the arc length corresponding to a segment of the unit hyperbola. Therefore, the independent variables of the $\sin_p$ and $\cos_p$ functions are also a type of arc length, which we can define within the unit circle like trigonometric functions.

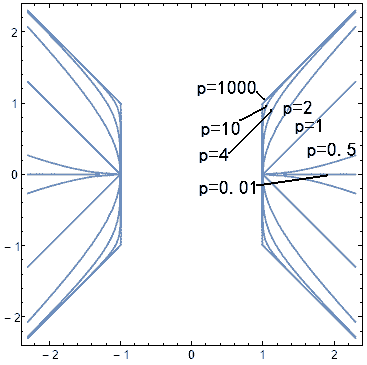
Let’s look at the graphs of these strange generalized trigonometric functions: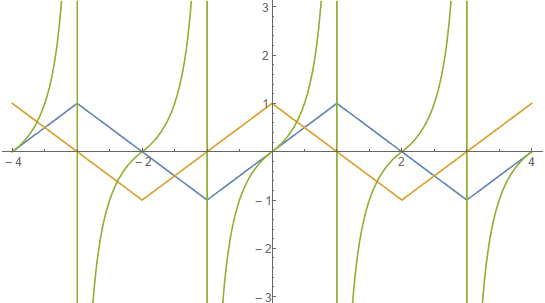


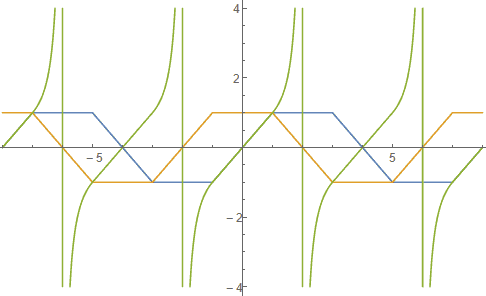
They are all piecewise functions. The sine and cosine have a somewhat square-like feel, while the curve segments in the tangent function are like inverse proportion functions.
To plot non-special cases like p=0.5, 3, or 4, we first need to find formulas to calculate $\sin_p$ and $\cos_p$. We need to derive the differential equations they satisfy from their definitions. The independent variable of trigonometric functions is the angle, and the function values are the coordinates of the corresponding point on the unit circle. So, the question is, how do we define an angle in p-norm? When we encounter a seemingly unsolvable problem like this, we can think about a familiar situation, such as p=2. How do we define radians in a circle? A radian is defined as the arc length on the unit circle. However, when you studied hyperbolic functions, you may have heard of the concept of a hyperbolic angle, which explains the independent variable of hyperbolic functions as twice the area of a “sector” of the hyperbola. We can similarly define a radian as twice the area of a sector of the unit circle. It can be proven that for angles in a unit circle and hyperbolic angles in a hyperbola, these two definitions are equivalent (note that when defining the hyperbolic angle using arc length, the calculation requires the hyperbolic distance formula $d^2=(x_2-x_1)^2-(y_2-y_1)^2$, while the area calculation method remains unchanged). But for scenarios where $p$ is not equal to 2, are the angles defined by arc length and area still the same? Note that the arc length here must also be calculated using the corresponding p-norm distance formula. For the area, we will temporarily use the same method of calculation (by integration), but we cannot rule out the possibility that the method of calculating area has changed in p-norm space.

1. The safest approach is to use the arc length definition. After tedious calculations, we can obtain the following system of differential equations: (Note that we must include a sign function in our differential equations to carefully handle the absolute value symbol in the distance definition)
   $${d \sin_p x\over d x}=sign(\cos_p x)(1+|\sin_p x/\cos_p x|^{p(p-1)})^{1-p\over p} $$$${d \cos_p x\over d x}=-sign(\sin_p x)(1+|\cos_p x/\sin_p x|^{p(p-1)})^{1-p\over p} x $$$$ \sin_p(0)=0, \cos_p(0)=1$$

2. Based on the area definition, we can derive another system of differential equations:
   $${d \sin_p x\over d x}=sign((1-\sin_p^p x)^{1-p\over p})|(1-\sin_p^p x)^{1-p\over p}|=sign(\cos_p x)|\cos_p^{p-1} x| $$$$ {d \cos_p x\over d x}=-sign(1-\cos_p^p x)|(1-\cos_p^p x)^{1-p\over p}|=-sign(\sin_p x)|\sin_p^{p-1} x |$$$$ \sin_p(0)=0, \cos_p(0)=1$$

Trigonometric functions are a special case where p=2, and the solutions to both systems of equations are the same. With these differential equations, we can perform numerical calculations. The period of $\sin_p$ and $\cos_p$ is the circumference of the circle in the p-norm world, so the independent variable can take all real numbers.
The next question is naturally whether these functions can be analytically continued to the complex plane. For example, $\sin(i) = i \sinh 1 = 1.1752i$, which gives us a hint: complex numbers might be able to connect the trigonometric and hyperbolic functions in a p-norm world.
The following two hidden subsections will discuss the analytical properties of the generalized trigonometric functions defined by area. They are not very relevant to p-norm geometry, so feel free to skip them.

[Click to expand/collapse] Analytical properties of generalized trigonometric functions

Minkowski Space in p-Norms

Let’s look at the unit hyperbola $x^p-y^p=1$ in p-norm:

Because the expression defined by arc length is too complex, we will only discuss the generalized trigonometric functions defined by area here.
Using the same area method to define the generalized hyperbolic functions $\sinh_p$ and $\cosh_p$, we can similarly get the differential equations (here we assume we are in the first quadrant, so we omit absolute values and sign functions):
$${d \sinh_p x\over d x}=\cosh_p^{p-1} x $$$$ {d \cosh_p x\over d x}=\sinh_p^{p-1} x $$$$ \sin_p(0)=0, \cos_p(0)=1$$
Their forms only differ by a sign. Let’s recall the derivation process for the relationship between the familiar trigonometric and hyperbolic functions when p=2—it was obtained through Euler’s formula $e^{i\theta}=\cos \theta+i \sin \theta$, which in turn was obtained through the Taylor series expansion. We can perform a series expansion of $\sin_p$ at 0. To do this, we need to know all the higher-order derivatives of $\sin_p$ at 0. When p=2, the derivatives of the $\sin$ function are very regular: there are no even-powered terms in the Taylor series, and the odd-powered terms alternate in sign. $\sin_p$ is not easy to expand, as its derivatives are not regular, so we have to “brute-force” calculate them: for example,
$$(\sin_3 x)’=\cos_3^2 x\\
(\sin_3 x)’’=(\cos_3^2 x)’=-2\cos_3 x \sin_3^2 x\\
….
$$
This way, we can calculate the first few terms of the series: $\sin_3 x = x-4{x^4 / 4!}+160{x^7 / 7!}-20800{x^{10} / 10!}+…$
We notice that only terms with the power of (3n+1) exist! It can be proven by mathematical induction that the series expansion of $\sin_p x$ only contains terms with the power of (pn+1) and they alternate in sign. This means that $\sin_p(\omega x)=\omega \sin_p( x)$, where $\omega^p=1$, and similarly $\cos_p(\omega x)=\cos_p(x)$.

We can also calculate that the series expansion of the hyperbolic function $\sinh_p x$ also only contains terms with the power of (pn+1), and all coefficients are positive. These coefficients are equal to the absolute values of the corresponding coefficients of the trigonometric function $\sin_p x$! With this discovery, we can calculate $\sin_p(\omega x)=\omega \sinh_p(x)$, where $\omega^{2p}=1$ and $\omega^p=-1$. Complex numbers indeed connect trigonometric and hyperbolic functions.

Fermat Curves

For p=3, we have $\sin_3(\omega x)=\omega \sinh_3(x)$. Taking $\omega=-1$, we get $\sin_3(-x)=-\sinh_3(x)$. In principle, the sine function should be an odd function, but the Taylor series shows it is not. The reason is that we are studying the curve $|x|^3+|y|^3=1$. The absolute value leads to a piecewise function, and $\sin_3(-x)=-\sinh_3(x)$ is actually not valid. Since they are both piecewise functions, we cannot even discuss analytical continuation to the complex plane. If we abandon the absolute value and study the curve $x^3+y^3=1$ (red line in the figure below), it becomes immediately clear why hyperbolic and trigonometric functions appear together: it corresponds to a circle in the first quadrant and a hyperbola in the second and fourth quadrants. This is the intention behind not writing absolute values and sign functions at the beginning of this section.

After abandoning the absolute value, $\sin_3 x$ and $\cos_3 x$ are called Dixon’s elliptic functions, denoted as sm(x) and cm(x). Elliptic functions are a class of magical complex functions with two periods. Their period on the real number line is not the circumference of the circle, but 3/2 times the circumference. For a detailed explanation, you can refer to Wikipedia and this paper.
However, for even p, $\sin_p x$ and $\cos_p x$ are indeed periodic (with the period being the circumference of the circle), but their analytical continuation is multi-valued. These functions are called generalized Dixon elliptic functions.

Finally, I want to say that the generalized Dixon elliptic functions defined by area are actually a type of 2-norm thinking, simply studying the algebraic curve $x^p+y^p=1$, which has nothing to do with p-norm. However, the differential equations for generalized trigonometric functions defined by arc length are too complex, so their analytical properties will not be studied for now.

Pi and Trigonometric Functions in Different Norms

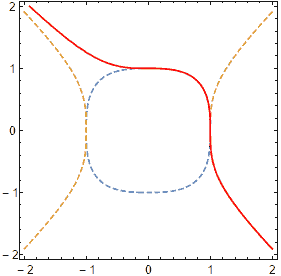
How much do the generalized trigonometric functions defined by arc length and area differ? The most obvious difference is that the period of the trigonometric functions is not the same—this period corresponds to the circumference and area of the corresponding circle. When $p=1$, the area of the circle (diamond) is 2, and when $p=\infty$, the area of the circle (square) is 4, but their circumferences are both 8. This shows that these two definitions are absolutely not equivalent. In fact, as you can see from the figure below, they are only equal when $p=2$. (Both are 3.1415926..) The red curve also reaches a minimum value of $\pi$ at p=2! (Here is the proof)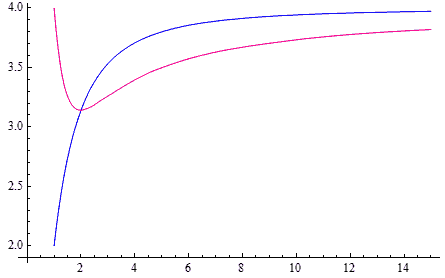

For various trigonometric functions, let’s rescale the x-axis to unify the periods and only focus on the difference in the shape of the function graphs to see how different they are: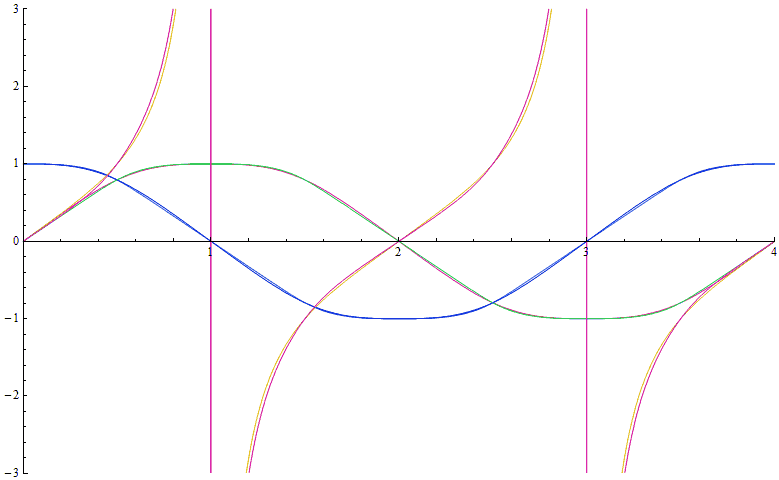

The figure above shows the sine, cosine, and tangent function graphs for p=5 using both definitions, a total of 6 curves. We find that the two curves, although not identical, are relatively close.

Rotational Symmetry

Returning to geometry, we can guess that p-norm also has a similar rotation matrix: $$\begin{pmatrix}
\cos_p\theta & \sin_p\theta \\
-\sin_p\theta & \cos_p\theta
\end{pmatrix}$$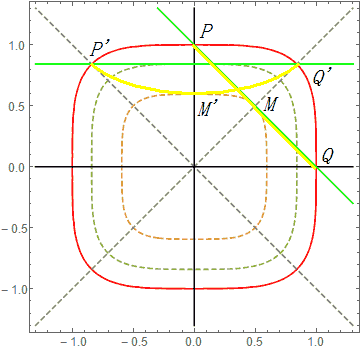

Note that here we must strictly choose the generalized trigonometric functions defined by arc length. Unfortunately, it can be verified that such a matrix transformation does not preserve length. Furthermore, we can verify that this transformation is not linear, for example, a line segment PQ rotating to P’Q’: (rotating 1/8 of a circle) The length of PQ is $2^{1\over p}$, while the length of P’Q’ is $2^{p-1\over p}$. We find that they are only equal when p=2. But this does not mean that rotation is impossible. In fact, a line segment is not necessarily a line segment after rotation; for example, the midpoint of PQ will rotate to a position below P’Q’. From the perspective of the isometry group (i.e., all transformations that preserve the distance between all points in a figure), this world can no longer rotate (it has no rotational symmetry). The isometry group only includes translation and reflection transformations. But this does not prevent us from defining a generalized “rotation”—a counterclockwise rotation of angle $\alpha$ around the origin:
$$r=\sqrt[p]{|x|^p+|y|^p}$$$$
\theta=atan2_p(y,x)$$$$
x’=r \cos_p(\theta+\alpha) $$$$
y’=r \sin_p(\theta+\alpha) $$
Where $atan2_p$ is similar to the $atan2$ function: it represents the angle of the vector $(x,y)$ with respect to the positive x-axis (the absolute value equals the arc length of the subtended arc).

For example, here is the rotation for p=3: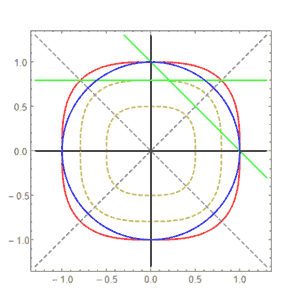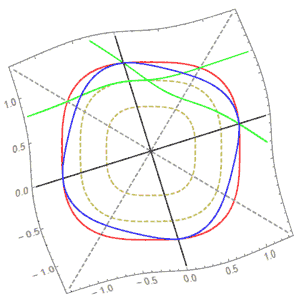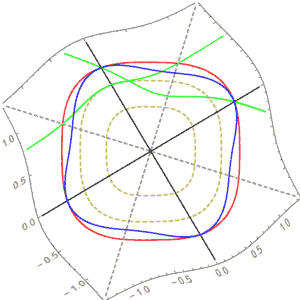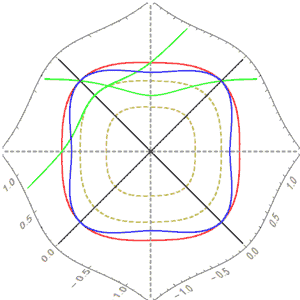

We see that it is not linear, and the “circle” remains unchanged under rotation, making it indeed the most perfect shape. (The blue circle of our world would deform in this world and would not be perfect.)
The following animation (for a p=3 world) can reflect the “bad“ properties of this rotation: we first translate a shape a certain distance, then rotate it clockwise by an angle $\alpha$ around the origin, then translate it back to the origin, and finally rotate it back counterclockwise by angle $\alpha$. The shape should not change in principle, but this rotation causes the shape to deform.

Below are the results of a series of deformations as the angle $\alpha$ changes continuously:

The period of this deformation is $\pi_3/2$ ($\pi_3$ is the pi in the p=3 world), and points on the line in the direction of translation do not move. Does this mean that objects in this world can only translate and not rotate? Because attempting to rotate would change the distance between certain points, and creatures in this world would consider rotation an incredible event. But we have ignored one point: objects in the world are not necessarily rigid bodies. Below, we will establish the simplest spring-mass model to examine the point-mass dynamics in this world. Spoiler alert: we will be surprised to find that we actually do not have the right to choose the p-norm value of p! It will automatically equal 2 in some sense.

Springs in a p-Norm World

What we usually call a rigid body, an object that does not deform at all, should be strictly defined as an object where the distance between its component points remains constant during motion. How do we keep the distance between parts of an object constant? The simplest approach is a stiff spring model: we divide the rigid body into countless point masses and connect every pair of them with a spring with a very large spring constant, where the springs’ natural lengths are exactly equal to the distance between the point masses. In this way, as soon as there is a change in distance, the point masses will be subject to a restoring force that tries to bring them back to their equilibrium positions. But this will cause the springs to oscillate, so we add an appropriate damping term to make the springs stop at the equilibrium position. This approximates a mechanical constraint of constant distance. Now let’s look at Hooke’s Law:
$$F = -k\Delta x$$where $\Delta x$ is the extension of the spring. Since it involves length, we naturally need to use the p-norm distance formula for the calculation, which gives us the spring model in a p-norm world.
First, we place a point mass on the x-axis at (1,0), connected to the origin by a spring (with a natural length equal to the distance from the point mass to the origin). Then we give it a velocity in the y-direction, and this point mass will start rotating counterclockwise around the origin. But since our equilibrium position is already defined using p-norm, the trajectory of the point mass is not a 2-norm circle, but a p-norm circle. At this point, we calculate the magnitude of the point mass’s velocity. Note that calculating velocity also requires using the p-norm length formula to calculate the length of the velocity vector. Unfortunately, the value of this velocity vector changes during rotation: when moving in the diagonal direction, the point mass’s speed is a bit slower than when passing through the x and y axes.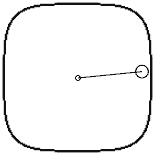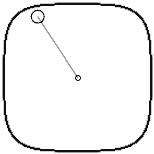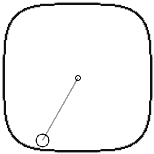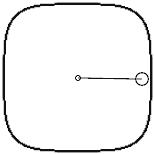

This is still fine. Let’s add another point mass at (0,1) on the y-axis, and connect it to both the origin and the point mass on the x-axis to form a triangle. Similarly, we give the point mass on the x-axis an initial velocity along the y-axis, and the two point masses will rotate together. But we find that this time, the motion speed of the two point masses is even more uneven. Note that in this space, we can no longer accurately define concepts like dot product and perpendicularity, so the so-called “orthogonal decomposition” cannot be performed. (Actually, with a bit more imagination, we can define a kind of “dot product” that maps p vectors into one number, so that the vector norm is still the p-th root of the vector’s inner product with itself, but it doesn’t seem to have any other meaning beyond that.)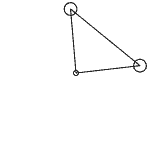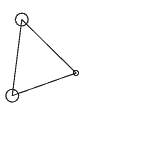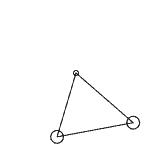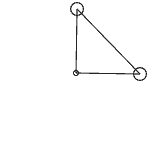

The two point masses in the figure seem to be dragging each other, but the lengths of the three sides of the constantly deforming triangle are indeed fixed! It seems that the criterion of three equal sides for congruence of triangles is also invalid under a general p-norm. Let’s add another point mass, this time on the diagonal of the x and y axes at (1,1), forming a square with the origin. We place springs between every pair of the four vertices, a total of 6. Now, if we give one point an initial velocity, will the square rotate? We said earlier that a world where p is not equal to 2 cannot rotate, so will the square really just translate? The calculation results are very strange: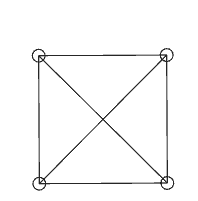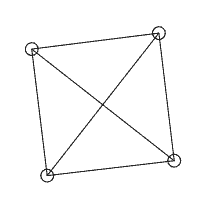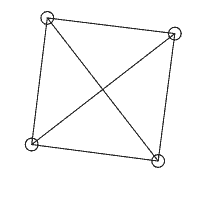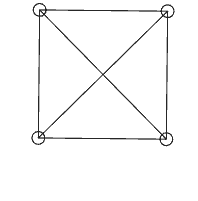

The square is still trying to rotate, and the initial rotation proceeds smoothly, but when the angle gets a little larger, we see the point masses start to jitter, which means the distance between the point masses can no longer be maintained at their original lengths and cannot automatically return to the equilibrium position. Even more mysteriously, after jittering for a while, the entire square suddenly rotates 90 degrees and stabilizes again (the numerical instability has already occurred, so subsequent stabilization has no physical meaning), but after a while, it suddenly rotates back, until the numerical calculation error becomes too large, causing the entire system to violently jitter and collapse. But we can see that this square does not obediently translate; it still wants to rotate, and when the length constraint is not satisfied, the internal forces produced by the springs cannot stop the rotational motion, causing the entire system to violently oscillate and collapse.

Let’s analyze a case of centrifugal motion: tie one end of a spring with a natural length of 0 to the origin and place a point mass at the other end. What happens if we give the point mass an initial velocity? Since the spring has no natural length, the magnitude of the force is simply the distance from the coordinate to the origin multiplied by the spring constant. Our only problem is how to decompose the force onto the coordinates. Note that given coordinates $(x,y)$, we can find the unit vector in this direction: $(x/\sqrt[p]{x^p+y^p},y/\sqrt[p]{x^p+y^p})$. Readers can verify that this vector has unit length and is parallel to $(x,y)$. Therefore, the result of the force decomposition is the unit vector multiplied by the length $l=\sqrt[p]{x^p+y^p}$ and then multiplied by the spring constant $k l$. This means the final expression for the force is $(kx,ky)$, and the expression is completely independent of $p$! What’s more, it’s “annoying” that as long as $\vec{F}=k\vec{x}$, the trajectory of the point mass will be a line segment, an ellipse, or a circle. Note that the circle here is a 2-norm circle, and it is a natural solution to the differential equation determined by $\vec{F}=k\vec{x}$. This means that no matter what norm we choose, the behavior of the final physical system will automatically satisfy the 2-norm! This also explains the special nature of the 2-norm and why fewer people have deeply studied p-norm geometry.

Celestial Motion in a p-Norm World

The spring $\vec{F}=k\vec{x}$ above is just a special case of central force motion. In general, we set $F=kx^n \vec{e}_x$, where n=1 gives Hooke’s Law and n=-2 gives the Law of Universal Gravitation (Hint: it’s an inverse-square law in three dimensions, not two). Writing out the unit vector gives $\vec{F}=k||\vec{x}||^{n-1}\vec{x}$. This means that only Hooke’s Law (n=1) is independent of the norm. For other values of p, the orbits of planets under gravity are different! Let’s look at a planetary system in a p-norm.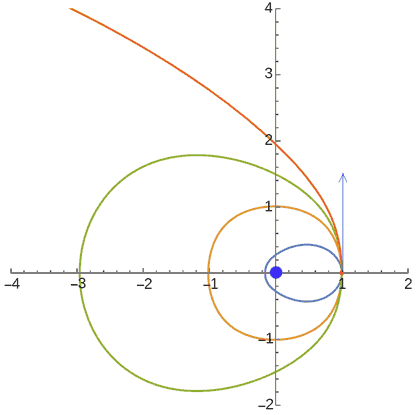

Calculations show that for p=4, the satellite’s orbit is stable! (Thanks to a helpful netizen for the correction (2023.01.01), I initially calculated it incorrectly and thought the orbit was unstable like an inverse-cube law). Just as in the 2-norm case, planets have both closed and open orbits. In the figure above, the Earth is at the origin, and a satellite at coordinate $(1,0)$ with an appropriate initial velocity (blue arrow direction) can achieve a “perfectly circular” orbit (orange-yellow). If the initial velocity is slightly smaller, it gets a flattened, elliptical-like orbit (blue). A larger velocity results in a more elongated elliptical orbit (green). If the velocity is too large, it reaches escape velocity and flies away (orange-red). All of this is so similar to the laws of celestial motion we know! However, it’s important to note that the orange-yellow “perfectly circular” orbit is not a 4-norm circle; their shapes have a slight difference, which we will discuss further later.
The inverse-square law decay is the universal and natural decay mode for forces (like gravity and electromagnetism) in three-dimensional space. As the decay exponent changes, p-norm orbits can also precess and form rosette-shaped orbits, just like in the 2-norm. However, as mentioned in the article “A Visit to the 4D World”, if the force decays as an inverse-cube law, only escape, crash, and “perfectly circular” orbits exist, and the “perfectly circular” orbits are unstable: any slight perturbation will cause them to either crash or escape. Calculations show that this conclusion still holds when the p-value in the norm is not 2, which suggests that choosing a different norm has little effect on orbit stability!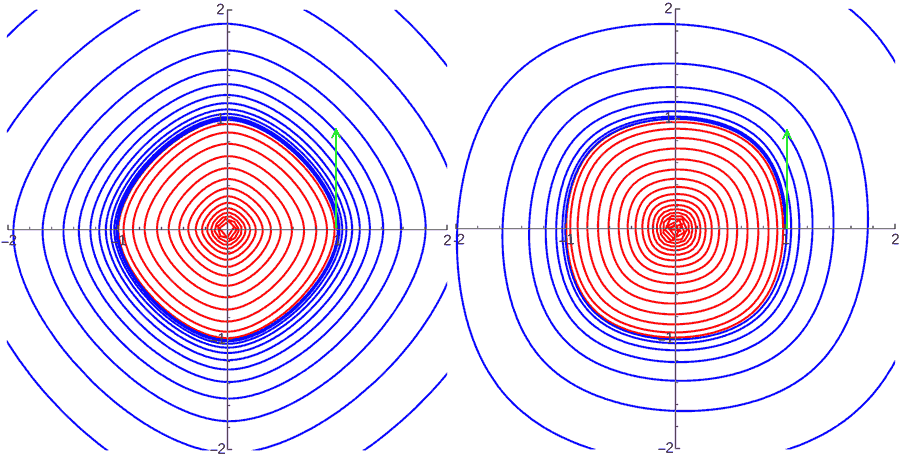

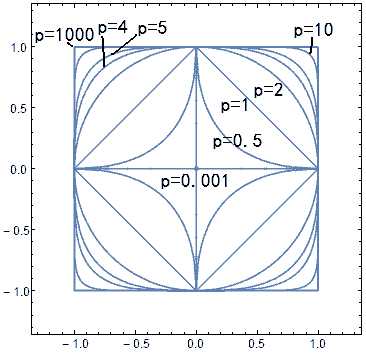
Even more magically, the shapes of these “perfectly circular” orbits are different in different situations! Let’s look at the difference between the “perfectly circular” orbits under inverse-square, inverse-cube, and inverse-10th power laws, the true “circles” in 10-norm and 1-norm spaces, and the relationships among them.

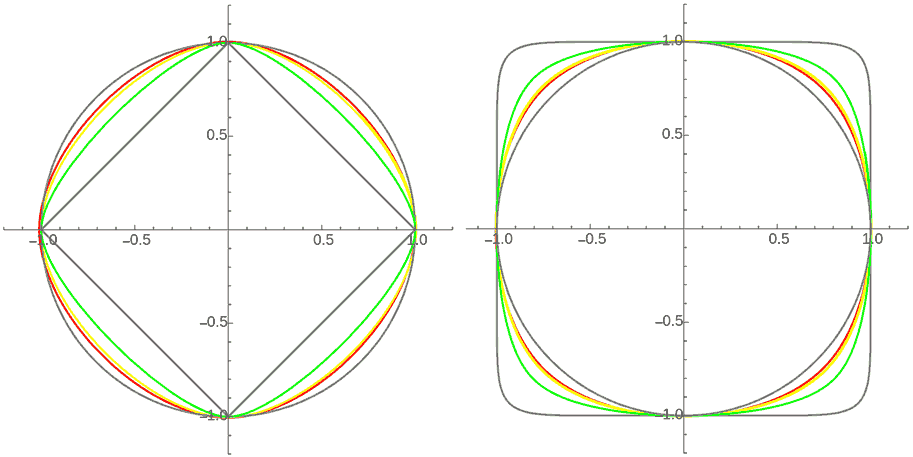
We can see that these stable orbits are all “smoother” than the p-norm circles (i.e., closer to the 2-norm circle). The larger the power of the gravitational decay, the closer the orbit is to the p-norm circle, and the smaller the power, the closer it is to the 2-norm circle (p-circle and 2-circle correspond to the two gray shapes in the figure). This is because when the decay power becomes as small as negative one, it becomes the perfectly circular case of Hooke’s law. However, is there an algebraic equation that can describe these intermediate orbits? They still look like generalized circles of the form $|x|^n+|y|^n=1$. Are they really generalized circles? If the inverse power n tends to infinity, does its stable orbit tend to the p-norm circle? These questions require further investigation.

Other Strange Geometries

We now have a preliminary understanding of p-norm space and geometry. So what is non-Euclidean geometry? Non-Euclidean geometry is actually also 2-norm space, but the space is not flat, causing the form of the length formula to depend on position, but it is always a quadratic form of the micro-elements. For example, the spherical distance formula is $ds^2=dx^2 \sin^2 y + y^2$, where the coordinates $(x,y)$ are latitude and longitude on the sphere. We call all spaces where the distance micro-element is always in a quadratic form (including curved ones) Riemannian geometry. In fact, spaces like p-norm that cannot define an inner product can also be curved; these are called Finsler geometry, a generalization of Riemannian geometry, or rather, Riemannian geometry is a special case of Finsler geometry. Finsler geometry is very strange, but most concepts from general Riemannian geometry can be extended to it. Besides the inability to rotate objects, you might also encounter situations where walking from A to B is a straight line (more accurately, a geodesic), but walking back along the same path is no longer a straight line! Below are some descriptions of Finsler geometry that I found on a Zhihu Q&A:

Finsler geometry is a geometry where the inner product on the tangent space is replaced by a general norm, so each tangent space is no longer an inner product space, but just a normed linear space.
If Riemannian geometry is compared to the situation on a real earth with mountains, valleys, and pits, where the shortest distance is no longer a straight line, then Finsler geometry is like an earth with a fierce hurricane, where going with the wind, against the wind, or sideways to the wind all have very different results.