In my previous articles on four-dimensional space, I described a world on a four-dimensional planet. This time, I’ll investigate the day-night and seasonal changes produced by a 4D planet’s rotation and revolution. Let’s assume this planet is approximately a hypersphere. The first thing we need to do is figure out how to describe a point on a hypersphere. This isn’t difficult - similar to spherical coordinates, we can use hyperspherical coordinates to construct a longitude-latitude-like representation. However, since the hypersphere’s surface is three-dimensional, we need three angular measurements.
Before discussing this planet’s rotation, let me briefly introduce rotation of objects in four-dimensional space: The biggest difference from 3D space is the existence of “double rotation.” Rotation is actually an effect unique to two-dimensional space: when rotating the xy plane, the trajectories of all points except the origin are circles in the xy plane. In 3D space, when rotating the xy plane, the projection of spatial points’ trajectories onto the xy plane is also a circle, but note that points on the z-axis don’t move - this is the axis of rotation. In 4D space, when rotating the xy plane, the projection of spatial points’ trajectories onto the xy plane is also a circle, but note that points on the zw coordinate plane don’t move. So we say that 4D space rotation is around a plane. Do you see the issue? The rotating coordinates are only x and y, but we’re concerned with the parts that don’t participate in the rotation, which leads to rotation axes and planes having inconsistent dimensions. Actually, 4D space has “double rotations” where everything except the origin is moving, which forces us to stop focusing on the non-rotating parts: if a rotation combines simultaneous rotations in both the xy and zw planes, this is called double rotation - this is possible because the two planes are absolutely perpendicular, movements in the two directions don’t interfere, and the rotation speeds can differ. It can be proven that all rotations in 4D space are either simple rotations with a stationary rotation plane, or double rotations where all points except the origin are moving, and each double rotation can be decomposed into a composition of two absolutely perpendicular single rotations. This article by Hadroncfy details point movement in double rotation.
Back to planetary rotation: In our universe, due to complex reasons during early formation, planets rotate to varying degrees. For 4D planets, double rotation is the most general state of rotation. We decompose the double rotation into a composition of two absolutely perpendicular single rotations. These two rotations don’t necessarily have equal speeds - we’ll define the faster rotation plane as the xy plane (red circle in the figure below) and the slower plane as the zw plane (red line in the figure below, which is actually also a circle, but appears as a line due to stereographic projection through pole $-w$). This establishes a 4D rectangular coordinate system. 
Note that the stereographic projection shows the hypersphere’s surface. The marked coordinate points are where the coordinate axes intersect the hypersphere’s surface. The coordinate origin is at the sphere’s center and cannot be represented in stereographic projection.
Now the problem arises: since the planet has no rotation axis, how do we define north and south poles? Simple - we artificially designate them, like choosing an observatory as the north pole? But while setting a 0° longitude is reasonable, completely “decreeing” poles like this seems excessive. We have another option: abandon the hyperspherical coordinate system and use another coordinate system on the hypersphere called Hopf coordinates, which naturally adapts to double-rotating planets.
| Hyperspherical coordinates: $$\begin{aligned} x&=r\cos \psi \\y&=r\sin \psi \cos \theta \\z&=r\sin \psi \sin \theta \cos \varphi \\w&=r\sin \psi \sin \theta \sin \varphi \end{aligned}$$ | Hopf coordinates: $$\begin{aligned}x&=\cos \xi _{1}\sin \eta \\y&=\sin \xi _{1}\sin \eta \\z&=\cos \xi _{2}\cos \eta \\w&=\sin \xi _{2}\cos \eta .\end{aligned}$$ |
- In the 3D world, planets have an equator. For every point on the planet (except the poles), the direction of planetary rotation is called east, and the opposite direction is west.
- In the 4D world, instead of looking for a 2D spherical equator, we take the intersections of the mutually perpendicular rotation planes with the planet’s surface (two red circles) as equators. This gives us two equators - the circle in the xy plane and the circle in the zw plane. The xy plane rotates faster, so we call it the fast equator; the zw plane rotates slower, so we call it the slow equator. For every point on the planet, the direction of xy rotation is called east, the opposite is west. The direction of zw rotation has no name - I’ll call it yin, and the opposite yang. These are a new set of directional terms for 4D space - you can change them if you don’t like them. (In English, some call them Marp and Garp.) Yin-yang is perpendicular to east-west.
Now we have one more direction on the 3D hypersphere surface to define (perpendicular to the previous two) - the north-south direction: For any point not on the two equators, north points toward the nearest point on the zw equatorial circle (R in the figure below), and south points toward the nearest point on the xy equatorial circle (Q in the figure below). They are opposite directions, perpendicular to east-west and yin-yang. Note that the south pole is no longer a point but the xy fast equator, while the north pole is the zw slow equator. Hereafter we’ll refer to these two perpendicular circles as the south and north poles (the two red circles in the figure).
So what do the meridians and parallels look like on the planet? Answer: They’ve partially appeared in the “Dimensions: A Walk Through Mathematics” film. Remember how stereographic projection creates a torus with four families of circles? That’s a constant-latitude surface (parallel) on the hypersphere, with the meridians on the torus being the east-west and yin-yang directions. 
We conventionally take the south pole xy fast equator as 0° and the north pole zw slow equator as 90°. The north-south direction spans only 90° rather than 180° total like Earth’s north and south latitudes! This is a peculiarity of Hopf coordinates (corresponding to $\eta$ in the formulas). But it makes sense - the xy and zw planes are absolutely perpendicular, and north-south latitude indicates distance from the two planes, so it ranges from 0 to 90°. What about longitude? Since on a 4D planet, like Earth, every point on the rotation circle has equal status, we must artificially define the 0° east-west meridian and 0° yin-yang meridian. These longitudes, like Earth’s, range from 0 to 360° (corresponding to $\xi_1$ and $\xi_2$ in the formulas). They are hemispheres, just as Earth’s meridians are semicircles.
Now let’s discuss day-night alternation on the planet: We assume, similar to Earth, that the sun is far from the planet, so sunlight can be approximated as parallel rays. Parallel light illuminates half the hypersphere while the other half is in darkness. Earth’s terminator line (circle) becomes a terminator surface (sphere) in 4D, dividing the hypersphere into day and night hemispheres. Day-night alternation occurs as the planet rotates, but people living near the south and north poles experience completely different day-night cycles: The south pole has the faster xy rotation plane with shorter days, called short days; the north pole has the slower zw rotation plane with longer days, called long days. In mid-latitude regions affected by both rotation speeds, daily duration varies between short and long. The two circular motions combine to make the sun’s trajectory as unpredictable as Lissajous figures. If the speed ratio is irrational, the sun’s trajectory never closes, somewhat like the chaotic era in “The Three-Body Problem.” (But this isn’t chaos - it’s completely predictable.)
Note that this planet also orbits the sun. Newton’s laws tell us its stable orbit must be a perfect circle, so we don’t need to worry about orbital double rotation. The orbit causes seasonal changes, but these seasonal patterns differ from our familiar spring-summer-autumn-winter. We’re most concerned with the latitude of the sun’s direct rays, because both longitude directions are rotation directions that get “smoothed out” - day-night alternation is the same (except for time differences, which we’ll discuss later). This is similar to Earth.
- When the sun directly illuminates the south pole fast equator, nowhere has long-day alternation. Short-day variation is most pronounced on the south pole equator, weakening northward until the entire north pole equator lies on the terminator surface, causing polar twilight at the north pole, similar to Earth’s poles during equinoxes.
- When the sun directly illuminates the north pole slow equator, nowhere has short-day alternation. Long-day variation is most pronounced on the north pole equator, weakening southward until the entire south pole equator lies on the terminator surface, causing polar twilight at the south pole.
If the sun’s direct rays are at mid-latitudes, everywhere has at least one type of day-night alternation, with no polar twilight and certainly no polar day or night. But how does the orbit move the direct ray point? On Earth this depends on the ecliptic-equatorial angle - the angle between the orbital ecliptic plane and Earth’s rotational equatorial plane. On this planet it also depends on the ecliptic-equatorial angle, but in 4D space two planes need two angle parameters to describe their relationship. Let’s say the orbital plane makes angles $\theta_1$ and $\theta_2$ with the south pole xy plane, then it makes angles $90°-\theta_1$ and $90°-\theta_2$ with the north pole zw plane. The angles are complementary because the xy and zw planes are absolutely perpendicular. The latitude of the sun’s direct rays is actually the line-plane angle between the sunlight direction and the south pole xy plane. As Earth rotates, the sunlight direction constantly changes, with all these directions parallel to the orbital ecliptic plane. We mentioned earlier that the two angles between planes mean the maximum and minimum line-plane angles of all directions in one plane with the other plane. This means the sun’s direct rays only fluctuate within the latitude range of $\theta_1$ and $\theta_2$, with a half-year period. Points in this range are tropical, while the rest are frigid zones. We call the time when the sun is at low latitudes the short-day season and at high latitudes the long-day season. I wrote a JavaScript program to simulate how the cosine of solar altitude angle varies with time at different locations on the planet. The figure below shows an orbital system where the ecliptic and polar planes are perpendicular ($\theta_1=0°$, $\theta_2=90°$, like the xz plane):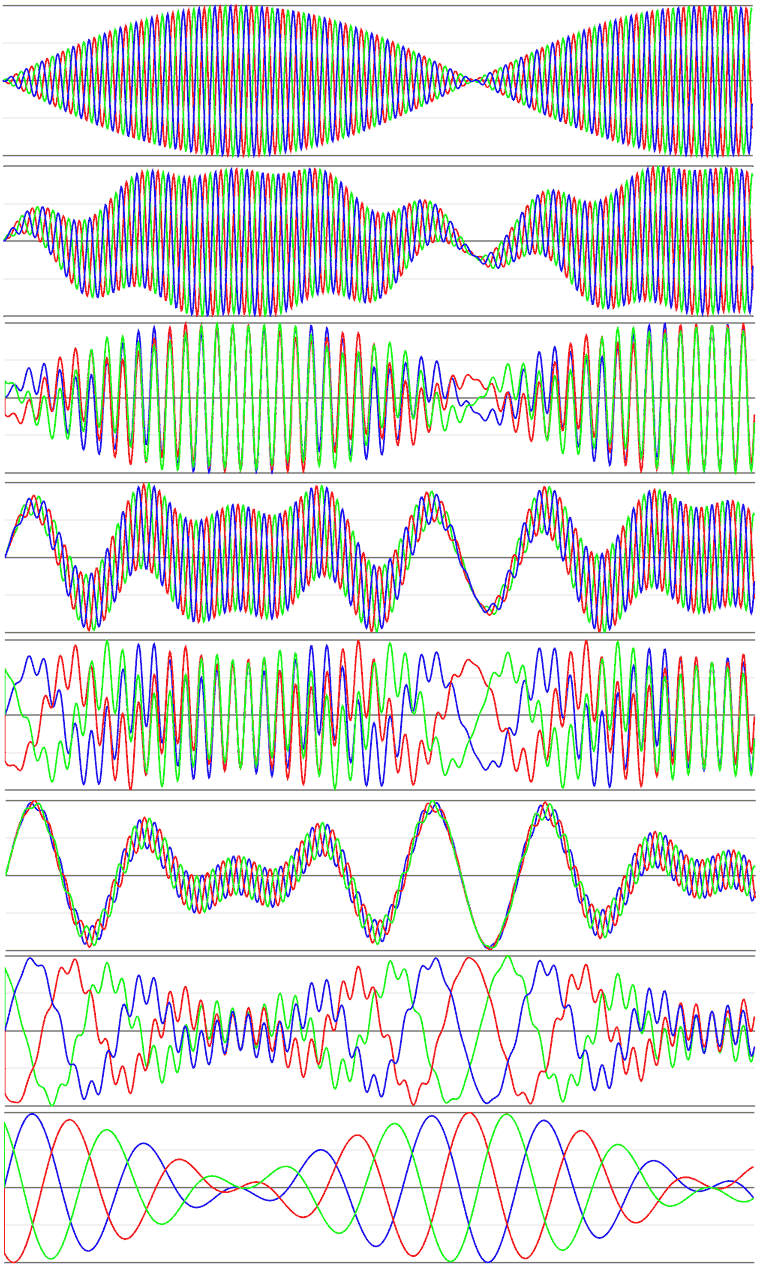
- 1: Three points on the south polar circle with 120° east-west longitude differences (corresponding to red, green, and blue lines): We clearly see short-day variation and time differences. Short-day variation is most pronounced when the sun is directly over the south pole. As seasons change and the sun moves to the north pole, short-day variation disappears and brief polar twilight occurs at the south polar circle.
- 2: Three points at 15° latitude with same yin-yang but 120° east-west longitude differences: Short-day variation is most pronounced when the sun is over the south pole, with no long-day variation. As seasons change and the sun moves to the north pole, short-day variation disappears but long-day variation becomes evident. At this time these three points are in the long day’s night, not quite polar twilight.
- 3: Three points at 15° latitude with same east-west but 120° yin-yang longitude differences: We see their short-day variation is identical with no time difference, but when the sun moves to the north pole and short-day variation nearly disappears, long-day time differences appear.
- 4, 5: 45° latitude regions: Similar to 15° latitude, except short-day variation when the sun is over the south pole isn’t as pronounced as at 15°, while long-day variation is clearly stronger when the sun is over the north pole.
- 6, 7: 75° latitude regions: Short-day variation is weak; long-day variation dominates.
- 8: Three points on the north polar circle with 120° yin-yang longitude differences: We clearly see long-day variation and time differences. Long-day variation is most pronounced when the sun is over the north pole. As seasons change and the sun moves to the south pole, long-day variation disappears and brief polar twilight occurs at the north polar circle.
For general orbital systems, both ecliptic-polar angles are between 0° and 90° and unequal, so everywhere always has at least one type of day-night variation. If the ecliptic-polar angles are equal (equiangular planes), the entire planet has no seasonal variation.
To summarize: Short-day and long-day variations depend not only on your latitude but also on the sun’s direct ray latitude (season). Long and short day variations result from these two factors combined. People on this planet need two calendar systems: long time and short time, with two different time zone divisions. The north-south time length differences cause people’s biological clocks to differ - only mid-latitude people can adapt to life everywhere, because mid-latitude regions are chaotic eras without patterns. Let’s discuss a special double rotation called isoclinic rotation: If the xy and zw planes rotate at the same speed, short and long days have equal duration. More interestingly, due to isoclinic rotation’s high symmetry, every point on the planet traces a circular path (these circles fill the hypersphere surface, forming a Hopf fibration! All circles are equiangular!). All these circles have equal status - any could serve as south or north pole equators! Unfortunately, nature has no such precise systems. More likely, the two rotation speeds are similar but differ slightly. This suffices to break the above symmetry and let us find unique south and north pole equators, because mid-latitude regions have both long and short time. This subtle speed difference gradually accumulates, causing long-time day/night and short-time day/night to become misaligned. If phases are completely opposite, polar twilight occurs, and this phenomenon may reverse periodically after a few days, analogous to beat frequency in physics.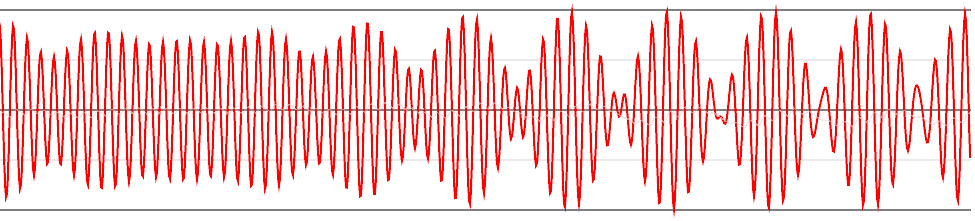 
Polar regions never have beat frequency, nor does it occur when the sun is directly over the poles, making this phenomenon quite extreme. Whether the sun sets depends on both short and long time, with their relative weights determined by latitude and season, making calendar systems on 4D planets truly complex.
Below is a JavaScript program for calculating solar altitude angles: (Best viewed on computer - I didn’t write mobile-friendly layout)
Next we’ll explore the planet’s magnetic field and 4D people’s compasses. But since magnetic fields are no longer vectors but 4D planar quantities like rotation (simple 2-vectors), plus complex 2-vectors similar to double rotation, involving exterior algebra and geometric algebra, we’ll stop here for now. Later I’ll write an article (Already written! Click here) specifically about electromagnetism in 4D space.
Update 2023
Along with the electromagnetic fields mentioned above, I created an interactive 4D planetary scene where you can dynamically observe the sun’s movement patterns on this planet and navigate with a compass:
- Click here to run
- If it doesn’t open, please refer to this tutorial.
The planet’s parameters are:
- Long day is 2.87 times the short day;
- The planet’s orbital period is 100 short days;
- The planet’s ecliptic-equatorial angles are 12 degrees and 43 degrees.