4D Space (I): Simple Geometric Solids

#This article discusses pure spatial Euclidean 4D geometry, not Minkowski 4D spacetime in physics! (Imagine if there were 2D beings, they might think of 3D as 2D space + time, which is 3D spacetime, not our 3D Euclidean geometric space) This article does not treat the 4th direction as time! Therefore, this article will not involve topics like relativity.

# This article is written for readers with a preliminary understanding of 4D space (e.g., knowing about tesseracts, etc.). If you are not yet familiar, I recommend the film “Dimensions: A Walk Through Mathematics“ (which has profoundly influenced my understanding of mathematics), and CFY’s article provides a more fundamental introduction to 4D space. (CFY and I researched 4D space together, so some introductions might overlap)

4D space is too abstract, so we cannot directly perceive it sensually (see or touch it directly). However, we can build an understanding of it using analogy or analytical methods. The analogy method is more intuitive but requires high imagination and is not rigorous; the analytical (calculation) method is rigorous but lacks intuitive geometric meaning, and its misuse can reduce geometry to algebra. Only by combining both can we better understand 4D space.

Tesseract and Tesseractoid

I won’t bore you with basic parameters like face shape, number of faces, vertices, etc. Let’s look at other properties:

• Like a cube, it is a prism, its “base cell” is a cube (i.e., “3D base”), and its height $h$ is equal to the edge length, which is also the side length of the base cell cube.
• It is a special “tesseractoid,” and a “tesseractoid” is a special 4-parallelotope.(parallel 8-cell. Analogy: cube, cuboid, parallelepiped).
• A tesseract with edge length $a$ cm has a “hypervolume” of $a^4$ cm⁴, and a “surface volume” of $8a^3$ cm³. (Analogy: cube volume and surface area).
• According to the Pythagorean theorem or coordinate calculation, the space diagonal (i.e., the distance between the two farthest points on the tesseract) of a unit tesseract is an integer: $\sqrt{4}=2$ (whereas for a cube it’s $\sqrt{3}$ and for a square it’s $\sqrt{2}$, which are irrational numbers).
• Many properties of a tesseractoid are similar to those of a cuboid. Its dimensions are described by four parameters: length $a$, width $b$, height $c$, and depth $d$. Its hypervolume is $abcd$, and its surcell volume is $2(bcd+acd+abd+abc)$.

General Prisms

A general prism is a geometric solid formed by extending (a.k.a extrusion) an arbitrary three-dimensional geometric shape as its base in a direction not within the three-dimensional space of the base. If this direction is perpendicular to the base, it is a right prism; otherwise, it is an oblique prism. For now, we will only discuss right prisms. This might be a bit abstract, but it’s okay, for example, we can still guess the volume formula: $V=Sh$. Below, let’s look at some specific examples: a cuboid-prism is a tesseractoid, right? We also have:

Cubinder (Cylindrical Prism)

A prism whose base 3D figure is a cylinder: let the base cylinder’s height be $h_1$ and radius be $r$, and the cubinder’s height be $h_2$. We can analogously deduce its hypervolume $= \pi r^2 h_1 h_2$. 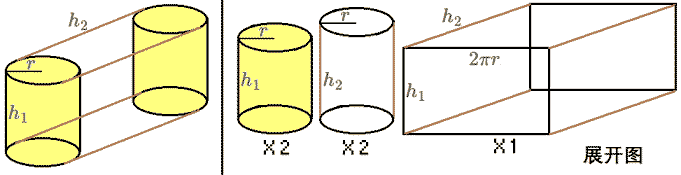Now for a challenging one: how to calculate the surface volume of a cubinder? It has a curved three-dimensional side surcell in 4D space! First, let’s recall the surface area of a 3D prism: two base areas plus the perimeter of the base multiplied by the height, $2S + Ch$. The reason the lateral surface area is the perimeter times height is that we can unfold the lateral surface of a prism, that is, cut it along a generatrix and flatten it into a plane, at which point the base unfolds into a line. So the side surface of a cubinder is similar, except it unfolds into a cuboid!
Base surface volume: $2\pi r^2 h_1$; side surface volume: the surface area of the base cylinder multiplied by the cubinder’s height, $(2\pi r^2+2\pi rh_1)h_2$. So the total surface volume $S = 2\pi r^2 (h_1+h_2) + 2\pi rh_1h_2$.

• Cubinder symmetry
  Haven’t you noticed, after seeing the unfolded diagram, volume, and surface area formulas for the cubinder, that the base cylinder height $h_1$ and the cubinder height $h_2$ have the same status? This implies that a cubinder, like a cuboid, can have any of its cylindrical faces chosen as its base. Don’t look at the other cylinder being slanted; it’s just a matter of perspective; viewed straight, it’s the same.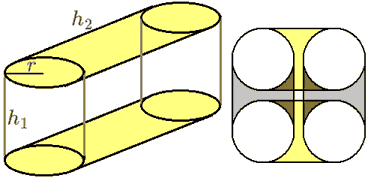
  
• Old friend from “Dimensions“: Stereographic projection
  In fact, using stereographic projection to project from four dimensions to three dimensions is only a method for displaying very special figures, because it only projects the three-dimensional sphere $\mathbf S^3$ onto three-dimensional space $\mathbf R^3$. Irregular figures (such as those with holes, depressions, or intersections) cannot be projected onto $\mathbf S^3$, so we generally use parallel projection or perspective projection. However, our cubinder is still relatively regular. Let’s have a look!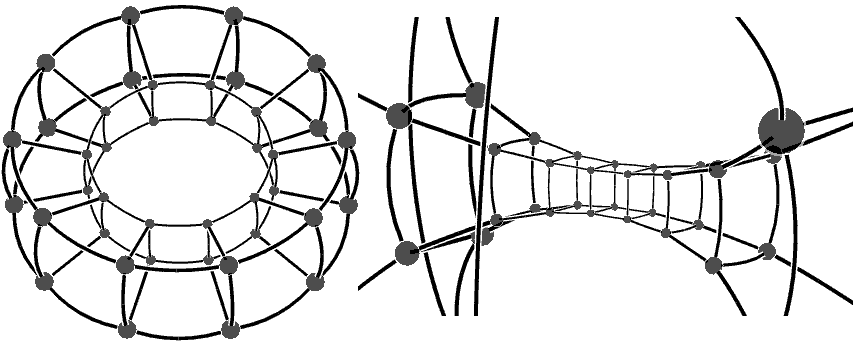 Screenshot from jenn3d software
  Hmm, a large cylinder containing a small cylinder, just like a tesseract has a large cube containing a small cube. The stereographic and perspective projections of all prisms, if viewed from the right angle, are larger shapes containing smaller ones. The right side shows a different view with a side face passing through the pole. (Actually, this is a decagonal prismatic prism; a true cubinder is an $\infty$-gonal prismatic prism).
  

Prismatic Prism

From the stereographic projection, we find that computers calculate cylinders by approximating them with prisms. Therefore, the properties of a prismatic prism are similar to those of a cubinder, except that the curved surface of the cylinder is gone, replaced by many very thin cuboids (like the red section in the image below). An $n$-gonal prismatic prism is enclosed by $4$ $n$-gonal prisms and $n$ cuboids, totaling $n+4$ cells. For example, a tesseract is a square prism (cube) prism, where $n=4$, and it has 8 faces.
How do we calculate the number of edges, 2D faces, and cells (3D faces) for any prism? Besides drawing and counting them one by one, we can derive them from the base cell: a point moves to form a line, a line moves to form a plane, a plane moves to form a solid. So the number of lateral cells (3D solids) equals the number of 2D faces of the base cell; these are all prisms with the corresponding 2D faces of the base cell as their bases (when the 2D faces of the base cell are curved surfaces, they form “curved cells”: curved 3D faces). The number of lateral 2D faces equals the number of edges of the base cell; these are all rectangles. The number of lateral edges equals the number of vertices of the base cell. Of course, when counting the total, don’t forget to include the two base cells.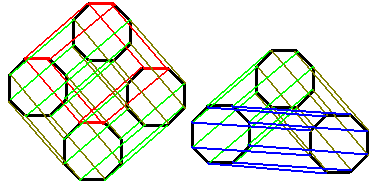

Look at the projection of an 8-gonal prismatic prism; it feels like 4 octagons whose corresponding points are connected to form 8 quadrilaterals, or it can be seen as 8 quadrilaterals whose corresponding points are connected to form 4 octagons. Let’s try something new: draw something where 3 octagons have their corresponding points connected to form 8 triangles. This is something we’ve drawn out of thin air. Does this thing still exist in 4D geometric space? The answer is definitely yes. Of course, this thing is no longer a prism; it can be explained by the direct product, which I will introduce in detail later.

Spherinder (Spherical Prism)

Its hypervolume is naturally the volume of the base sphere multiplied by the height. What about its surface volume? We would naturally think of the surface area of the base sphere multiplied by the height. That’s correct, but there’s a small problem here: a sphere cannot be unfolded into a plane in three-dimensional space, so its side surface cannot be unfolded. This means that the side surfaces of prisms in 4D space cannot always be unfolded like those in three dimensions! Because the two-dimensional base of a three-dimensional prism can always be stretched into a line, but this is no longer the case. Of course, this does not prevent us from calculating the surface volume, because we can subdivide the sphere into infinitely many small prisms and sum them up, and the result is still the surface area of the base sphere multiplied by the height.
Later, we will analyze and discuss how spherinders, cubinders, and hyperspheres can roll on a table in 4D space, providing an intuitive feel for this magical 4D world.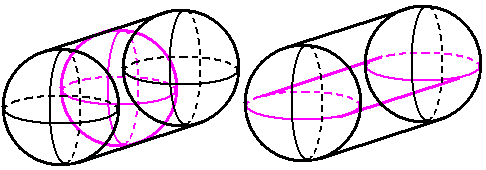

Various Pyramids

A pyramid is a geometric solid formed by selecting a point anywhere outside the three-dimensional space of an arbitrary three-dimensional geometric base, and connecting this point to all vertices of the base.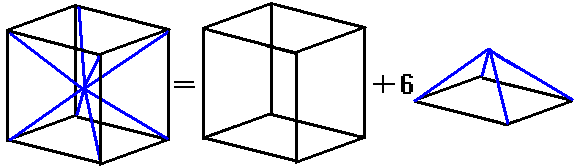

Similarly, how do we calculate the number of edges, 2D faces, and cells (3D faces) for any pyramid? The number of lateral cells (3D solids) is still equal to the number of 2D faces of the base cell, but they are all pyramids with the corresponding 2D faces of the base cell as their bases. The number of lateral 2D faces equals the number of edges of the base cell; these are all triangles. The number of lateral edges equals the number of vertices of the base cell. When counting the total, the base cell must also be included.

Hypervolume and Surface Volume of Pyramids

When I was in elementary school, my teacher and textbooks explained the cone volume formula like this: put a cone and a cylinder with equal base and height into a cup full of sand to measure their volumes, and found that the cone was exactly $\frac{1}{3}$ of the cylinder’s volume, without any explanation. Later, this problem was explained using Zu Geng’s principle and calculus. The formula for the hypervolume of a 4D pyramid is $V=\frac{1}{4}Sh$, which can be proven with calculus; the proof is omitted. (For an $n$-dimensional pyramid, the formula is $V=\frac{1}{n}Sh$).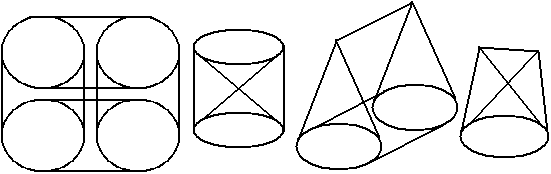

Cubinder(Cylindrical prism), Cylindrone(Cylindrical pyramid), Coninder(Conic prism), and Dicone(Conic pyramid). Can you identify which cells they are bounded by? Their hypervolume formulas are respectively: $$V_1=\pi r^2h_1h_2, V_2=\frac14\pi r^2h_1h_2, V_3=\frac13\pi r^2h_1h_2, V_4={\pi\over12} r^2h_1h_2$$ How do the surfaces of a dicone and a cylindrone unfold? Don't know? Then calculate the surface area by integration.

One can imagine that higher-dimensional space must also contain cubindrical pyramidal pyramids, prismatic prismatic pyramidal pyramids, etc. Fortunately, we are not in those insane dimensions!

Congratulations, you now have the level of geometric understanding of a 4D elementary school student! In the next section, we should learn middle school geometry and go read the works written by Euclid in their civilization!