Minkowski Space and Constant Curvature Spaces

Today we will look at a series of worlds constructed based on Minkowski space and introduce some related concepts of differential geometry. Many peculiar worlds have a certain connection with it. This article is more about the geometric properties of these spaces. Later, we will discuss what the astronomy and daily life of the inhabitants in these worlds are like. A spoiler in advance: the Minkowski world is both strange and familiar to us.
According to conventional understanding, the distance formula between two points in a Cartesian coordinate system is: $$s^2=(x_2-x_1)^2+(y_2-y_1)^2$$ We call this ordinary flat surface a two-dimensional Euclidean space, denoted as $\mathbb{R}^2$, or simply Euclidean space. The next step is to define a circle, which is the set of points at a fixed distance from the origin. Therefore, the equation for a circle is: $x^2+y^2=R^2$
Besides the p-norm worlds mentioned earlier, are there any other possible worlds with different distances on a plane? For example, why must the squares be added? What would happen if they were subtracted? That is:
$s^2=(x_2-x_1)^2-(y_2-y_1)^2$
A space that uses this kind of distance is called two-dimensional Minkowski space, denoted as $\mathbb{R}^{1,1}$, or simply Minkowski space. The circle in this space becomes a hyperbola:
$x^2-y^2=R^2$
The hyperbola is the most symmetrical and perfect shape in this space!
Why would anyone want to construct such a space? Because in advanced mathematics, there are hyperbolic functions (you should have heard of them). We will see that in this space, hyperbolic functions will replace the status of trigonometric functions! Back to the distance formula, it is obvious that the most special thing about this space is that the squared distance between some points becomes negative, and taking the square root results in an imaginary number. A simple analysis shows that the points in the yellow region below have an imaginary distance to the coordinate origin, while the points in the white regions on the left and right have a normal real distance to P, and the distance is 0 on the gray boundary. What is a world with this kind of distance metric like? Do these imaginary and real distances intertwined have any meaning? Before we continue to discuss the significance of this world, let’s look at the mathematical properties of this space.

Hyperbolic Functions and Hyperbolic Angles

General advanced math textbooks directly give the expressions for the hyperbolic sine $\mathrm{sinh}(\alpha)$ and hyperbolic cosine $\mathrm{cosh}(\alpha)$ as their definitions:
$$\mathrm{sinh}(\alpha)={e^{x}-e^{-x}\over 2}$$ $$\mathrm{cosh}(\alpha)={e^{x}+e^{-x}\over 2}$$What is the relationship between these exponential functions and sine, cosine, and hyperbolas? In fact, the above definition does not reflect the essence of hyperbolas. Below, we will introduce the geometric definition of hyperbolic functions. Trigonometric functions can be defined within a unit circle. Similarly, hyperbolic functions can be defined within a “unit” hyperbola (calculus can show that they are the same as the exponential expressions above). We know that in the most natural radian system, the independent variable of a trigonometric function is the central angle, and its value is equal to the arc length it corresponds to, and also half of the area of the sector it encloses.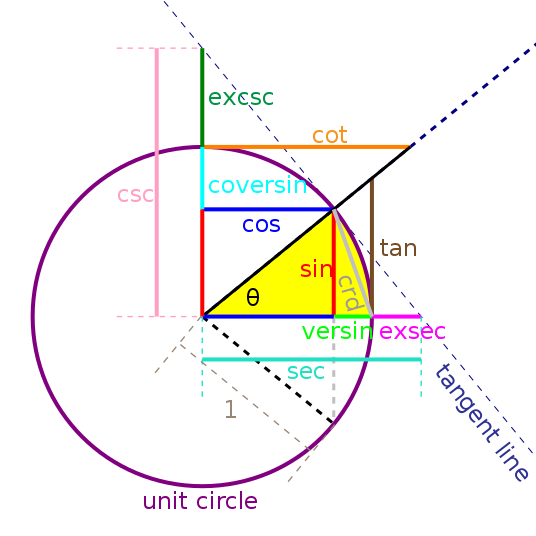

Calculus shows that for a hyperbola, the ratio of the arc length to the sector area is not a constant. However, if we use the Minkowski length metric to calculate the hyperbolic arc length, this “arc length” is exactly half of the area! This indicates that the unit hyperbola is not a very symmetrical shape under the normal Euclidean distance metric. From now on, we will study this hyperbola in a new distance metric space (the Minkowski metric), where it is the “circle”!

Distance Formula and Metric

For the length of any curve, we must first calculate the length of an infinitesimally small segment $\mathrm{d}s=\sqrt{\mathrm{d}x^2-\mathrm{d}y^2}$ and then integrate. (This can be understood by considering that when the line is very short, $x_1-x_2=\mathrm{d}x$). This differential form of the distance formula is called a metric tensor or metric, and its scope of application is much wider than the distance formula between two points. We will use the term metric from now on, and no longer say distance formula. Thus, the metric corresponding to the normal Pythagorean theorem is written as $\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{d}y^2$, while the Minkowski metric is $\mathrm{d}s^2=\mathrm{d}x^2-\mathrm{d}y^2$.

Hyperbolic Angle

We naturally think of using this arc length as the independent variable for hyperbolic functions. The hyperbolic angle labeled $\alpha/2$ in the figure below, where $\alpha$ is actually the area of the yellow “hyperbolic sector.” The most natural understanding of the independent variable of hyperbolic functions is a kind of angle, but it is a new hyperbolic angle defined in Minkowski space! The sine and cosine values of the angle are defined the same way as for trigonometric functions: they are the values of the y-coordinate and x-coordinate.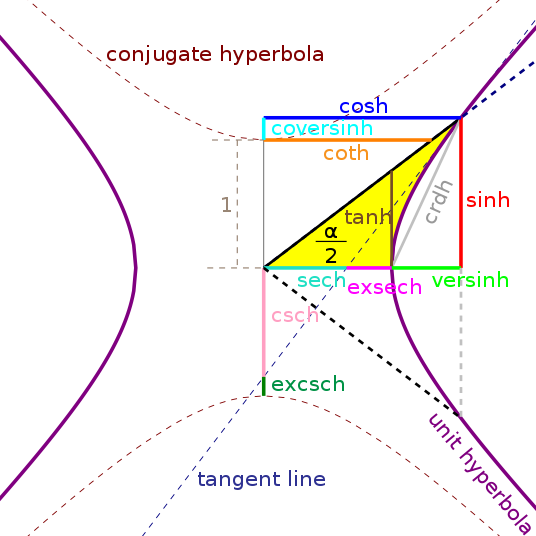

“Hyperbolic Rotation” in the Minkowski World

The hyperbola should be the most perfect and symmetrical shape in this world, so it should have some kind of “rotational” symmetry. This rotation must preserve the Minkowski distance between all parts of the shape, and is called “hyperbolic rotation” or “pseudo-rotation.” Similar to circular angles, we use hyperbolic angles to measure the size of a hyperbolic rotation. A reminder again: the arc length for a hyperbolic angle must be calculated using the Minkowski distance. We must try to abandon the Euclidean distance view to better adapt to this world. For those who don’t want to see the derivation of the rotation formula, you can click here to skip directly.

How do we define a rotation that keeps the hyperbola invariant? Given a hyperbolic angle, let’s see where the point $(1,0)$ on the x-axis rotates to, i.e., find the coordinates of the endpoint of a segment of a given arc length. According to the definition of hyperbolic functions, the new coordinates should be $(\mathrm{cosh}(\alpha),\mathrm{sinh}(\alpha))$. How do we calculate the coordinates of an arbitrary point $(x,y)$ rotated by a hyperbolic angle $\alpha$? Based on our experience in Euclidean space, polar coordinates are convenient for rotation, so we also define a polar coordinate for a hyperbolic angle: it is represented by the Minkowski distance $r$ from the point to the origin and the hyperbolic angle $\alpha$ with the positive x-axis. Given $(r,\alpha)$ in polar coordinates, we can convert to Cartesian coordinates using hyperbolic functions, i.e., $(r \mathrm{cosh}(\alpha),r \mathrm{sinh}(\alpha))$. Conversely, given Cartesian coordinates, how do we calculate polar coordinates? First, the distance is $r=\sqrt{x^2-y^2}$. The calculation of the angle is similar to trigonometric functions. From the proportionality of corresponding sides in similar triangles, it’s not hard to find that the hyperbolic tangent value of the hyperbolic angle $\alpha$ is $y/x$, i.e., $y/x=\mathrm{sinh}(\alpha)/\mathrm{cosh}(\alpha)=\mathrm{tanh}(\alpha)$. Let’s denote the inverse function of $\mathrm{tanh}$ as $\mathrm{artanh}$, so $\alpha=\mathrm{artanh}(y/x)$. Solving the equation gives the specific expression for the inverse hyperbolic tangent function $\mathrm{artanh}(x)={1\over 2}\mathrm{ln}({1+x\over 1-x})$.
Okay, now we can finally calculate the coordinates of a point $(x,y)$ rotated by a hyperbolic angle $\beta$ around the origin: first convert to polar coordinates, add the angle $\alpha$, then convert back to Cartesian coordinates. Done!

1. Cartesian to polar coordinates: $\alpha=\mathrm{artanh}(y/x)$, $r=\sqrt{x^2-y^2}$;
2. Rotate by hyperbolic angle $\beta$: $\alpha’=\alpha+\beta=\mathrm{artanh}(y/x)+\beta$, $r’=r=\sqrt{x^2-y^2}$;
3. Convert back to Cartesian coordinates: $x’=r’\mathrm{cosh}(\mathrm{artanh}(y/x)+\beta)$, $y’=r’\mathrm{sinh}(\mathrm{artanh}(y/x)+\beta)$;

The above expressions can be simplified. We will use the hyperbolic sum and difference formulas similar to those for trigonometric functions, which are easy to prove by substituting in the exponential function definitions. (Note the cosine formula has a minus sign for trigonometric functions)
$$\mathrm{sinh}(A+B)=\mathrm{sinh}(A)\mathrm{cosh}(B)+\mathrm{cosh}(A)\mathrm{sinh}(B)$$ $$\mathrm{cosh}(A+B)=\mathrm{cosh}(A)\mathrm{cosh}(B)+\mathrm{sinh}(A)\mathrm{sinh}(B)$$ Simplifying gives:$$x’=r’(\mathrm{cosh}(\mathrm{artanh}(y/x))\mathrm{cosh}(\beta)+\mathrm{sinh}(\mathrm{artanh}(y/x))\mathrm{sinh}(\beta))$$
Here we encounter hyperbolic functions nested with inverse hyperbolic functions. Based on the geometric meaning, it is clear that $x=r \mathrm{cosh}(\mathrm{artanh}(y/x))$ and $y=r \mathrm{sinh}(\mathrm{artanh}(y/x))$. Since $r’=r$, we get:$$x’=x \mathrm{cosh}(\beta)+y \mathrm{sinh}(\beta)$$Similarly, simplifying $y’$ gives:$$y’=x \mathrm{sinh}(\beta)+y \mathrm{cosh}(\beta)$$

From the expressions, we find that hyperbolic rotation, like normal rotation, has a linear relationship between the dependent variables $x’$, $y’$ and the independent variables $x$, $y$. This means it is a linear transformation—a straight line remains a straight line after rotation, unlike the non-linear distortion produced by rotations in a general p-norm space. This is an important property of hyperbolic rotation. (Note: A rotation formula can also be derived in p-norm space this way, but it will get stuck because trigonometric functions do not have sum and difference formulas that can be simplified.)

Side Note: Complex Numbers, Hyperbolic Functions, and Hyperbolic Complex Numbers

Here I want to talk about some interesting topics about the relationship between hyperbolic functions and complex numbers. This section is quite independent, so you can skip it and continue reading here if you want.

You may have heard of Euler’s formula for complex numbers:$$e^{\theta i}=\mathrm{cos}(\theta)+i\mathrm{sin}(\theta)$$This equation shows that the exponential function is periodic on the imaginary axis, and its values always rotate on the unit circle. This natural special treatment of the circle is intolerable to the inhabitants of Minkowski space, so they would want to modify the formula so that hyperbolic functions appear on the right side of the equation, allowing the function values to move along a hyperbola in the complex plane. But is this possible? From the expressions for hyperbolic functions, it is not difficult to find:$$e^{x}=\mathrm{cosh}(x)+\mathrm{sinh}(x)$$But this is a formula in the purely real number field, which cannot draw a hyperbolic trajectory on the complex plane. Not fun! Is there any other way? The answer is to modify complex numbers! The imaginary unit assumes that $i^2=-1$. If we change this and assume a different imaginary unit $j^2=1$, but where $j$ is not equal to $1$, we get a system of algebra similar to complex numbers called hyperbolic complex numbers. Euler’s formula in this system is indeed the hyperbolic sine and cosine:$$e^{\theta j}=\mathrm{cosh}(\theta)+j\mathrm{sinh}(\theta)$$It is worth mentioning that in the hyperbolic complex number system, the modulus is still calculated by multiplying a number by its conjugate, for example, $|x+jy|^2=(x+jy)(x-jy)=x^2-y^2$. This length is exactly the Minkowski distance on the hyperbolic complex plane! It can also be proven that if we view the point $(x,y)$ as a point $z = x+jy$ on the hyperbolic complex plane, the rotation operation is equivalent to multiplying the complex number $z$ by $e^{j\beta}$! This is similar to the widespread use of complex numbers in electrical engineering to simplify calculations involving the phase angle of alternating current. The use of hyperbolic complex numbers will also greatly simplify calculations related to hyperbolic rotation!

The only major difference between hyperbolic complex numbers and normal complex numbers is that there are many numbers with zero length whose reciprocals do not exist. For example, $1+j$, the reciprocal of this number is $${1\over 1+j}={1-j\over (1+j)(1-j)}={1-j\over 0}$$It is clear that in hyperbolic complex number division, any number with a length of zero cannot be a divisor!

The Strange Directions of the Minkowski World

Next, we will explore the spatial properties of this world through hyperbolic rotation. First, the biggest difference between a hyperbola and a circle is that the latter is a finite, closed figure. Although a hyperbola looks infinitely large, is it finite under the Minkowski distance metric? Calculations show that the hyperbola is also infinitely long under the Minkowski metric, so hyperbolic functions are not periodic like trigonometric functions, and hyperbolic rotation is also not periodic. Second, since rotation keeps distances invariant, points with an imaginary distance to each other will still have an imaginary distance after rotation. Since the origin is not special compared to other points, we can classify the vectors originating from any point in space: they are divided into three regions of direction based on whether the Minkowski length of the vector is greater than zero, imaginary, or equal to zero. Any rotation will not change the length of a vector, so this division of directions is an inherent property of the space. It will not change even if the coordinate system is rotated. For convenience, let’s temporarily call them real directions, imaginary directions, and zero directions. Note that the properties of these directions are of an essential nature and are independent of the choice of coordinates. You cannot transform a direction of one nature into another by rotation! As a result, some shapes we consider conventional will become very strange. A good old circle would be cut into several curves of different natures. It’s hard to imagine what kind of chaotic things one would encounter living in such a world, or rather, does such a world really have any meaning?

We All Live in a Minkowski World

However, the Minkowski world, which seems not at all beautiful, is indeed a real physical world system. In fact, we are all in it. It is our spacetime! If we don’t consider the curvature of spacetime, the four-dimensional Minkowski world $\mathbb{R}^{3,1}$ is exactly the world studied by relativity. The two-dimensional Minkowski space we just discussed corresponds to a two-dimensional spacetime model. Below, we will reveal its connection to spacetime.

Two-dimensional Spacetime

For simplicity, let’s start with a low dimension. On a plane, let the x-axis be the spatial direction and the y-axis be the time direction. We can use a curve to represent the spacetime trajectory of a particle in a one-dimensional world over time, which is called the particle’s worldline. By convention, the particle is placed at the origin at a certain time. If the particle is stationary, its worldline is a straight line coinciding with the y-axis. If it has a velocity $v$ relative to the reference coordinates, the worldline becomes a slanted line $y=x/v$. Choosing natural units where the speed of light is 1, the worldline of a photon is $y=\pm x$, which are those straight lines of zero direction. This seems a bit far-fetched, but we will immediately introduce relativity: relativity states that the speed of light is constant in any reference frame. Einstein derived relativity from this. The property of hyperbolic rotation not changing the direction means that no matter how you rotate, the zero direction remains the zero direction. This is the geometric interpretation of the constancy of the speed of light in relativity! Since this blog is not a physics popularization site, there are already very detailed popular science resources online. I won’t go into the specific details here, but the clearest video on Bilibili combining Minkowski geometry is probably this one: 《Special Relativity, but Visualized》 (highly recommended!!). Below, I will translate the statements of relativity into geometric language:

1. The transformation between different velocities in relativity is called the Lorentz transformation, which is what we just called hyperbolic rotation:
   Translation: Just look at the GIF below to get a feel for it: using a moving object as a reference frame, when the object accelerates or decelerates, the time axis needs to be rotated so that the y-axis in this reference frame is always tangent to the worldline. Note that the animation superimposes a translation along the curve and a hyperbolic rotation.

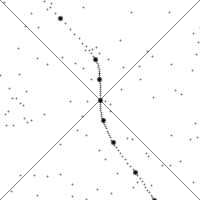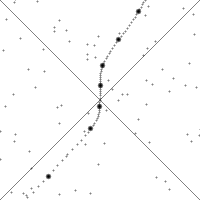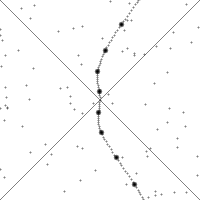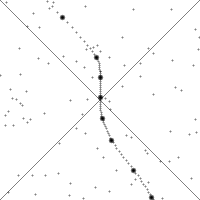
2. The speed of any object cannot exceed the speed of light:
   Translation: The worldline of a stationary object is a straight line parallel to the time axis, the y-axis, and its direction is timelike. Choosing a reference frame with a different velocity is actually rotating the coordinates of spacetime. According to the geometric properties of rotation, a timelike direction is always timelike, and the absolute value of the curve’s slope is always greater than 1, which means the speed is always less than the speed of light. Also, since rotation is not periodic, a coordinate system can be rotated at a uniform hyperbolic angular velocity indefinitely, so an object, from its own perspective, can accelerate uniformly forever but still cannot reach the speed of light.

3. The distances in spacetime can be divided into three categories: spacelike, timelike, and lightlike (or null):
   Translation: The division of distances between two points into real, imaginary, and zero categories has a clear physical meaning. A real distance means the two points have a spatial interval, and a reference frame can always be found to transform them to the spatial x-axis. We call this a spacelike (or null) direction. An imaginary distance indicates the two points have a time interval, and a reference frame can always be found to transform them to the time y-axis. This direction is called timelike. A zero distance indicates that the two points have a “lightlike“ interval, because the speed calculated from the slope is the speed of light in any reference frame. The worldline of any massive particle is always timelike, and the worldline of a massless particle (such as a photon) is always lightlike. There are no particles with a spacelike worldline; their existence would violate the causal structure of spacetime.

4. The length of a particle’s worldline is the proper time experienced by that particle, which is the passage of time as it feels it.
   Translation: When a particle is stationary, its worldline coincides with the y-axis, so the length of the worldline between two points is the same as the time difference between the two points, called proper time. Hyperbolic rotation does not change the length of a shape, so the proper time (length) remains constant, while the coordinate time (y-coordinate value) changes.

5. When an object moves, it experiences length contraction and time dilation:
   Translation: By using hyperbolic rotation, it’s not difficult to see the coordinate components in the new coordinate system. For the specific construction method, you can refer to the video on visualized relativity mentioned above.

6. The concept of simultaneity is relative, and different reference frames may have different views on what is “simultaneous”:
   Translation: It is impossible for a rotated coordinate system to only move one axis. The time axis has rotated its direction, and the spatial axis will naturally also move (unlike the Newtonian view of spacetime). In the new coordinate system, the surfaces of simultaneity also become slanted. It is, of course, not guaranteed that two points with the same time coordinate in one frame will also have the same time coordinate value in another frame. The classic relativity paradoxes such as the garage paradox and the pole-in-the-barn paradox arise from this. For details, refer to the video on visualized relativity mentioned above.

Four-dimensional Spacetime

For our four-dimensional spacetime, the distance metric is $\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2-\mathrm{d}t^2$, meaning only the square of the time component has a negative sign. The number of positive and negative squared terms in the distance formula are 3 and 1, respectively, so four-dimensional spacetime is denoted as $\mathbb{R}^{3,1}$. According to this notation, two-dimensional Euclidean space $\mathbb{R}^2$ can actually be seen as a shorthand for $\mathbb{R}^{2,0}$. A general n-dimensional Minkowski space is $\mathbb{R}^{n-1,1}$, so four-dimensional spacetime is a four-dimensional Minkowski space. Let $x^2+y^2+z^2-t^2=0$, and we get a conical surface of a sphere. The Minkowski distance of points on this cone relative to the origin is zero. They are the boundary separating the timelike and spacelike intervals. This is the famous light cone of relativity.
This light cone is a unique feature of Minkowski space. The fact that the squared distance can be positive or negative leads to the division of spacetime points into three categories: spacelike, timelike, and lightlike, causing the entire universe to be in a state of separation. A description by Liu Cixin in The Three-Body Problem is quite vivid:

The universe is a patient with high-level paraplegia—because of the speed of light, the universe has always been 16 billion light-years in scale and still expanding, but the speed of light is only 300,000 kilometers per second, which is terribly slow. This means that light can never travel from one end of the universe to the other. Since nothing can exceed the speed of light, information and forces from the other end of the universe can never reach this end. If the universe were a person, it would mean that no nerve signal could travel through its entire body, and its brain would not know about the existence of its other limbs. What is this if not a paraplegic patient? In fact, I have an even worse impression: in my eyes, the universe has transformed from an object of all beauty and faith into an expanding corpse.

It is worth noting that the four-dimensional space series discussed on this blog before were Euclidean pure spaces $\mathbb{R}^{4,0}$. A four-dimensional world that includes time is a five-dimensional Minkowski space (spacetime) $\mathbb{R}^{4,1}$. Be careful not to confuse it with four-dimensional spacetime $\mathbb{R}^{3,1}$.
In four-dimensional Minkowski space, the hyperboloid is the most symmetrical shape. Does it have any special physical meaning? If it were possible to tile a hyperboloid with regular repeating shapes like on a sphere, would we get a kind of time crystal? I thought about it and can only say that particles starting from the origin and reaching points on the hyperboloid experience the same proper time (the Minkowski distance is a constant), but besides that, there is nothing special about it. I believe such a structure would not naturally exist in the universe. On a side note, the curves we drew before, which were a mixture of timelike (imaginary directions) and spacelike (real directions), also have no physical meaning. Note that from now on, we will use the recognized standard terms spacelike, timelike, and lightlike instead of the temporary terms real directions, imaginary directions, and zero directions.

“Spheres” in Three-dimensional Minkowski Space

The fact that “spheres” in Minkowski space have no physical meaning does not mean they have no mathematical meaning. As we saw earlier, the “circle” in two-dimensional Minkowski space $\mathbb{R}^{1,1}$ is a hyperbola. So, the “sphere” in three-dimensional Minkowski space $\mathbb{R}^{2,1}$ is a hyperboloid. Unlike in two dimensions, the three-dimensional hyperboloid has two cases: a one-sheet hyperboloid and a two-sheet hyperboloid. Note that the following discussion about three-dimensional Minkowski space assumes the z-axis is the time direction and the x and y axes are the spatial directions.

Two-sheet hyperboloid

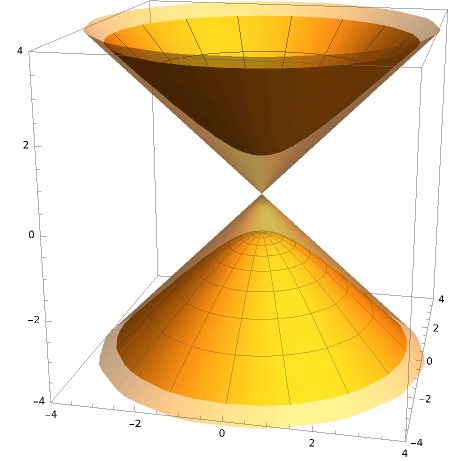
$$x^2+y^2-z^2=-1$$This equation is for a two-sheet hyperboloid. It can be seen as being formed by rotating a spacelike hyperbola on the $xz$ plane around the $z$-axis. The two asymptotes of the hyperbola rotate to form the conical light cone. What other geometric properties does this hyperboloid have? In Minkowski space, the most important thing is to distinguish the types of directions. What types of directions exist along the surface of the hyperboloid? Recall that tangent vectors on a sphere are always perpendicular to the radial direction. We guess the same is true for the hyperboloid, except that “perpendicular” here is defined in the new Minkowski space. Two vectors are perpendicular if their inner product is 0. In Euclidean space, the inner product of vectors is defined as $\langle(x_1,y_1,z_1),(x_2,y_2,z_2)\rangle=x_1x_2+y_1y_2+z_1z_2$. In Minkowski space, it becomes $\langle(x_1,y_1,z_1),(x_2,y_2,z_2)\rangle=x_1x_2+y_1y_2-z_1z_2$. We can verify that a vector perpendicular to a timelike vector must be spacelike, and all tangent vectors on the hyperboloid are perpendicular to the “radial” direction. These radial directions (from the origin to a point on the hyperboloid) are all inside the light cone, making them timelike imaginary directions. Therefore, all directions on this hyperboloid are spacelike, and the length of all tangent vectors is a positive real number.

Optional reading: Note that a vector perpendicular to a spacelike direction is not necessarily timelike. In spaces with more than one dimension, other perpendicular spatial directions naturally exist. Consider a case where the time dimension is greater than 1; a vector perpendicular to it would not necessarily be a timelike vector. What about a direction perpendicular to a lightlike direction? Since the distance for a lightlike direction is zero, its inner product with itself is 0, so by definition it is perpendicular to itself!

Do you remember the non-Euclidean geometry mentioned earlier when we introduced hyperbolic space? For a long time, this geometry that did not satisfy the parallel postulate was considered a mere logical sophism with no practical geometric meaning. Later, it was discovered that spherical geometry was the first practical implementation of non-Euclidean geometry: the abstract points and lines in Euclid’s Elements correspond to points on the sphere and great circles whose center is the center of the sphere. Why are great circles considered “lines” on the sphere? Here are two reasons:

1. The shortest distance between two points is a straight line. By using complex calculus of variations, it can be calculated that the shortest curve between two points on a sphere (except for antipodal points) is always the minor arc of a great circle.
2. A great circle is the “straightest” curve on a sphere. It only bends because it must be confined to the curved surface.

To distinguish them from true straight lines, these straightest lines on a curved surface are called geodesics. This term may have come from geodesy, the practical applied science from which spherical geometry originated.
We have to ask, if the geodesics on a sphere are great circles, what are the geodesics on a hyperboloid? The answer is: great hyperbolas! Imagine at the point $(0,0,1)$, what would the geodesics in the direction of the $x$-axis and the $z$-axis be? Following the logic of spherical lines, it must be the straightest line locally. Therefore, it is reasonable to believe that these geodesics are the intersections of the $xz$ and $yz$ planes with the hyperboloid, and these intersections are indeed hyperbolas. The z-axis of the hyperboloid is an axis of rotational symmetry, so we can imagine that all hyperbolas obtained by slicing the hyperboloid with a plane passing through the z-axis are the straightest geodesics. What if the point is at an arbitrary position? We can use a hyperbolic rotation centered at the origin to rotate it from the z-axis. Note that hyperbolic rotation is linear, so a plane that originally passed through the origin will still pass through the origin after rotation. Therefore, all the “straight lines” on the hyperboloid are “great hyperbolas” obtained by slicing the hyperboloid with a plane passing through the origin. This is similar to how the lines on a sphere are great circles, which are obtained by slicing the sphere with a plane passing through its center. See how everything is so similar between the sphere and the hyperboloid!
Note that because this hyperboloid discards the timelike and lightlike directions, it is essentially a curved pure spatial geometry similar to a sphere (pure space means that it looks locally like $\mathbb{R}^{2,0}$), which is called hyperbolic space. Hyperbolic geometry and spherical geometry are very similar. Using a method similar to stereographic projection, this space can be perfectly drawn in two dimensions (the projection results in the famous Poincaré disk model). I wrote about it a long time ago in my blog post Hyperbolic Space - Mathematical Art. It has a property that is the opposite of the sphere: on a sphere, 0 lines can be drawn parallel to a given line through a given point. On a hyperboloid, there are infinitely many! We can try to visualize this with a plane cut! 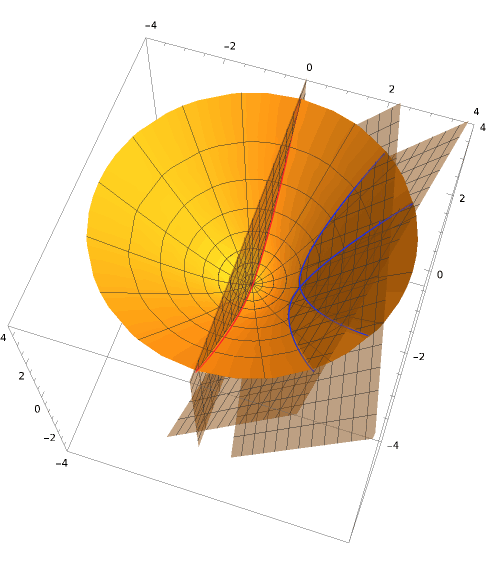We will not go into detail on the other properties of this space. There is still more geometry in Minkowski space waiting for us.

One-sheet hyperboloid

$$x^2+y^2-z^2=1$$This equation is for a one-sheet hyperboloid, and the difference from the two-sheet hyperboloid is the sign on the right side of the equation. It can also be seen as being formed by rotating a timelike hyperbola on the $xz$ plane around the $z$-axis. The two asymptotes of the hyperbola also rotate to form the conical light cone. The properties of the one-sheet hyperboloid are quite different from the two-sheet hyperboloid. In the figure above, if we choose the point $(1,0,0)$, we can move in two directions: the $y$ and $z$ directions. It is clear that these two directions are one spacelike and one timelike. Therefore, the space on the one-sheet hyperboloid is still a kind of spacetime, meaning it looks locally like $\mathbb{R}^{1,1}$. It is not hard to imagine that for any given point, we can still construct a light cone passing through that point on the hyperboloid. In fact, it is a constant-curvature curved spacetime, and these concepts help scientists study the overall structure of the universe in general relativity.

Since this is a spacetime, a set of reference frames should be established to observe the entire spacetime. For example, at the point $(0,1,0)$, we can establish a local spacetime coordinate system with the $x$-axis as the spatial axis and the $z$-axis as the time axis, where defining the spatial axis also defines the “simultaneous” lines. Note that the time axis is an infinitely long hyperbola, but the spatial axis is a finite circle. Therefore, we can think of this as a one-dimensional universe that is spatially a closed circle! The observer’s perceived state of rest is moving along the time axis. In flat Minkowski spacetime, as time passes, the observer’s spacetime coordinate system as a whole translates along the time axis. But here, translating along the time axis on the curved surface actually corresponds to a hyperbolic rotation. Why? Think about spherical geometry: translating a shape on a sphere is equivalent to rotating it around the center of the sphere. So it is not difficult to understand that on a hyperboloid, it is also a rotation. This hyperbolic rotation will rotate the original circular spatial axis into a long ellipse (note that it only looks stretched, the actual Minkowski distance has not changed). Three-dimensional rotation has a rotation axis, and Minkowski space is no exception. Therefore, we see that these spatial coordinate axes are no longer parallel after being translated. Instead, they all intersect at the point on the rotation axis! And as the observer moves farther away, this ellipse will eventually appear to approach the lightlike geodesic originating from the point on the rotation axis. A strange thing happens: from the perspective of a stationary observer in this spacetime, as time passes, time at a point at a specific spatial distance from them does not pass. Time is frozen? In fact, this is just an effect brought about by the coordinate system we have artificially established. In reality, that point is outside the light cone emitted from all points on the time axis, so that point will never have any causal connection with the observer, and there are no actual physical effects.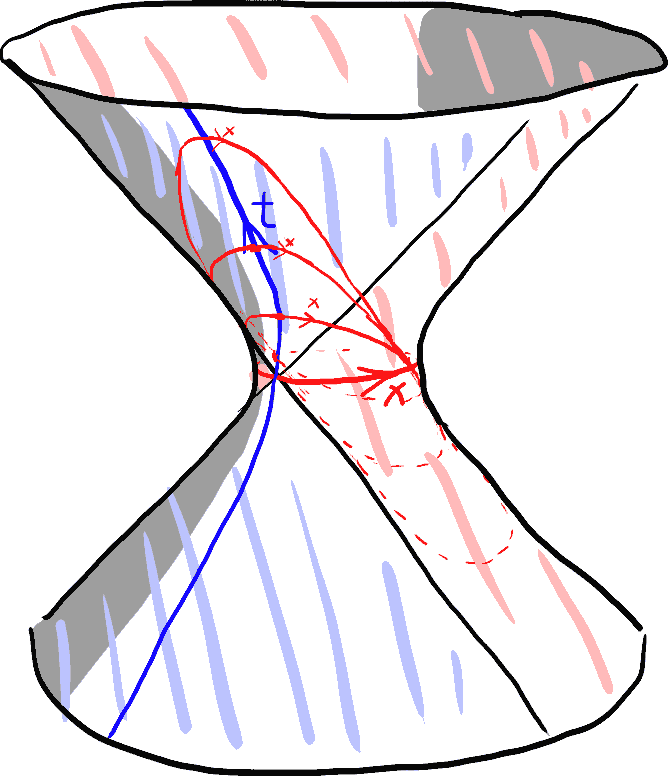

This phenomenon is not mysterious. Similar to the geodesics on a sphere, where two geodesics that were originally parallel end up intersecting, an extra angle appears (this is a hyperbolic angle!). This effect is actually evidence of the existence of curvature in this spacetime!
One more thing that might be confusing is that it seems the size of the universe seen by the observer in the figure above is at its minimum because the red simultaneous line happens to be wrapped around the narrowest part of the entire hyperboloid. However, as time passes, our perception of the cosmic space is the ellipse in the figure, which is gradually stretched and always passes through a fixed point, not the enlarging circular latitude grid lines in the figure below. So the size of the universe never changes at any given time. But in a certain sense, this universe is indeed expanding: two adjacent longitudes represent the worldlines of two observers who are currently stationary at a distance from each other. As time passes, the spatial distance between them will increase, and the length of the latitude circle segment between them will increase exponentially (it’s actually a hyperbolic cosine). Note that the centers of these latitude circles are not at the origin and they are not geodesics. Only geodesics can be used to measure “distance.” They are only close to geodesics, and the growth trend is the same. Think about a similar scenario on a spherical geometry: the latitude segments between longitudes get smaller as you go towards the North Pole. Although they are not geodesics, the distance between longitudes (measured by geodesics) does indeed decrease. This phenomenon, which causes geodesics that are initially parallel to eventually diverge, also comes from spacetime curvature effects.

Okay, these are the two types of “spheres” in three-dimensional Minkowski space: one-sheet and two-sheet. To understand the geometry of the real universe, three-dimensional spacetime is not enough. The real universe is four-dimensional spacetime. If we want to find a curved spacetime model, we need to consider the “spheres” in five-dimensional Minkowski space!

de Sitter / Anti-de Sitter Spacetime

You may have heard about research on the shape of the universe. The shape here actually refers to curvature. How do scientists know the curvature of the universe? Scientists use technical means to measure the angle between us and some distant galaxies, and determine the curvature based on the relationship between the sum of the angles of a triangle and 180 degrees. Experiments show that within the range we can measure, our universe appears to be very flat, so it corresponds to four-dimensional Minkowski spacetime. What would happen if the universe had curvature? This led to the birth of these two spacetime models:

1. de Sitter space is a four-dimensional constant-curvature spacetime with positive curvature, and the universe is closed, with a finite spatial volume.
2. Anti-de Sitter space is a four-dimensional constant-curvature spacetime with negative curvature, and the universe is infinite in both space and time.

Below, we try to construct them in a five-dimensional space.

de Sitter Spacetime

The first thing we think of is starting with a five-dimensional Minkowski space $\mathbb{R}^{4,1}$. That is, a hyperboloid under the metric $\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2+\mathrm{d}w^2-\mathrm{d}t^2$. If we choose the two-sheet hyperboloid:$$x^2+y^2+z^2+w^2-t^2=-1$$we will get a four-dimensional pure geometric hyperbolic space $\mathbb{H}^4$, which is no longer spacetime.

If we choose the one-sheet hyperboloid:$$x^2+y^2+z^2+w^2-t^2=1$$we do get a kind of four-dimensional spacetime. Let $t=0$, and the space at this moment is $x^2+y^2+z^2+w^2=1$, which is a three-dimensional sphere. This shows that spatially, this is a closed three-dimensional universe with a finite spatial volume. It is a four-dimensional de Sitter spacetime with positive curvature. In fact, we have already shown a two-dimensional de Sitter spacetime on a one-sheet hyperboloid, so we will not expand on its properties;

I wonder if anyone, like me, initially has this doubt: isn’t the most intuitive model for a spherical universe a hyperspherical cylinder $\mathbb{S}^3\times \mathbb{R}$ with a hypersphere $\mathbb{S}^3$ as the base and the time axis as the height? Why must time be curved along with space? The answer is simple: in such a universe, there exists a special stationary reference frame, which is the reference frame with the direction of the hyperspherical cylinder’s height as the time axis. If we only consider Newtonian mechanics, we can ignore the curvature in the time direction.

To summarize, the constant curvature spaces that can be constructed in $\mathbb{R}^{4,1}$ are the four-dimensional hyperbolic space and the four-dimensional de Sitter spacetime:

• Going from five-dimensional Minkowski space to a two-sheet hyperboloid loses a time dimension, leaving four spatial dimensions.
• Going from five-dimensional Minkowski space to a one-sheet hyperboloid loses a space dimension, leaving three spatial dimensions and one time dimension.

Anti-de Sitter Spacetime

How do we construct Anti-de Sitter spacetime? We can see that the construction method for these constant curvature spaces is to lose one dimension in a higher-dimensional space. In reverse, if we add a spatial dimension to a 3+1 dimensional spacetime, we get a 4+1 dimensional spacetime. If we add a time dimension, we get a 3+2 dimensional spacetime! Imagine a space with 3 spatial dimensions + 2 time dimensions. As long as we compress one time dimension appropriately, we can also get a 3+1 dimensional spacetime! Although two time dimensions sound incredible in physics, in mathematics it is just a matter of changing a sign. The $\mathbb{R}^{3,2}$ space refers to a space with a metric:$$\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2-\mathrm{d}w^2-\mathrm{d}t^2$$We can construct a four-dimensional generalized hyperbolic hypersurface with the same signs. The sign on the right side of the equation also presents us with a choice similar to the one-sheet and two-sheet hyperboloids. How do we make the specific judgment? The answer is: see if it intersects with a specific coordinate axis.

1. $$x^2+y^2+z^2-w^2-t^2=1$$Let’s first look at this hyperbolic hypersurface. Based on the non-negativity of squares, it has intersections with all spatial axes ($x$, $y$, $z$ axes), but no intersections with any time axes ($w$, $t$ axes). Taking the $x$-axis as an example, the tangent space directions on the hypersurface near the intersection point should include all directions except the $x$ direction, i.e., two spatial directions ($y$, $z$) and two time directions ($w$, $t$). It seems we made the wrong choice, and inadvertently got a peculiar constant-curvature space with two spatial dimensions and two time dimensions.
2. $$x^2+y^2+z^2-w^2-t^2=-1$$Similarly, we can verify that this is indeed a 3+1 dimensional spacetime. It seems this is the correct choice. Let $t=0$, and we get $x^2+y^2+z^2-w^2=-1$. Its spatial shape is a three-dimensional hyperbolic space with negative curvature in four-dimensional Minkowski space. Therefore, it is indeed Anti-de Sitter spacetime.

In fact, there is a small detail in the construction of Anti-de Sitter spacetime: the hypersurface $x^2+y^2+z^2-w^2-t^2=-1$ has intersections with the timelike coordinate axes. Let’s choose the intersection with the $w$-axis. Then the neighborhood of this point in spacetime has all spatial directions and another time direction $t$. We can create a timelike geodesic along the direction of the $t$-axis. Since it is a geodesic, it should be a section from a plane passing through the origin. This plane must also be parallel to both the $w$ and $t$ axes, so it is the $wt$ coordinate plane itself. Substituting this into the hyperbolic hypersurface equation, setting all spatial coordinates to 0, we get the equation for this timelike geodesic: $w^2+t^2=1$, which is a circle! The existence of a closed timelike line in a physical system is very bad! It means that as time passes, a particle returns to its own past and becomes its past self, leading to a whole host of paradoxes. Let’s look at the two-dimensional Anti-de Sitter spacetime to make it more intuitive.

Two-dimensional Anti-de Sitter Spacetime

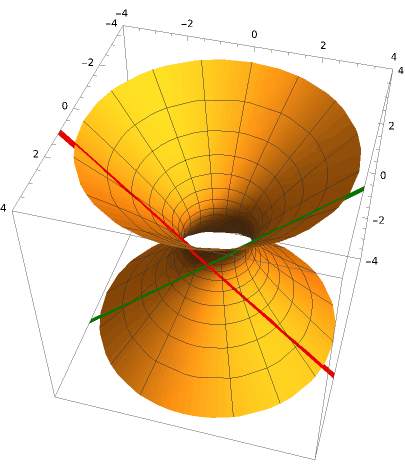
Two-dimensional Anti-de Sitter spacetime is 1+1 dimensional, so it can be obtained by constructing a hyperboloid in 1+2 dimensional space and reducing its dimension. The metric of $\mathbb{R}^{1,2}$ is $\mathrm{d}s^2=\mathrm{d}x^2-\mathrm{d}y^2-\mathrm{d}z^2$. The one-sheet hyperboloid $x^2-y^2-z^2=-1$ in this space is two-dimensional Anti-de Sitter spacetime.

You may have noticed that this is the same as two-dimensional de Sitter spacetime: taking the negative of both sides of $x^2+y^2-z^2=1$ gives $z^2-x^2-y^2=-1$, just a different arrangement of letters. In general, p+q dimensional space and q+p dimensional space have a wonderful symmetry: all time and spatial directions can be swapped between them. It is not difficult to verify that swapping the time and space axes of two-dimensional de Sitter spacetime gives two-dimensional Anti-de Sitter spacetime. The one-dimensional closed universe that was harmless spatially now has a closed curve in time, which is disastrous for physics.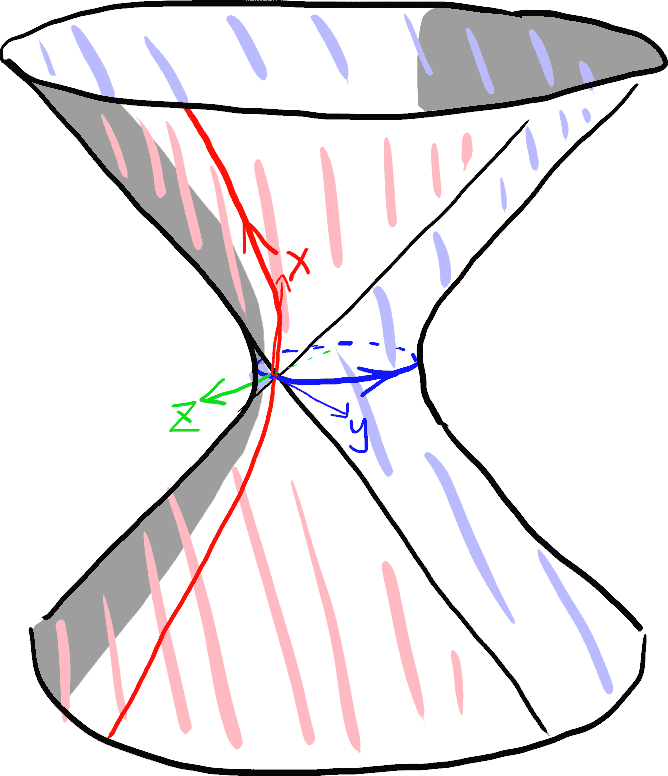

How can we avoid this problem? In fact, we are only concerned with the curvature of the universe. The hyperboloid model only corresponds to a negative curvature universe, not the overall topological structure. Since a circle is not a simply connected shape, we can use a topological concept called a covering space to construct a larger, simply connected space, resulting in a universe that is infinite in both time and space and has no closed timelike lines! Intuitively, this means we forcefully assume that after going around once, we arrive in a new world different from the original spacetime. A more vivid analogy is a hyperboloid-shaped roll of toilet paper. For the specific concept of covering spaces, you can refer to here. This method can be used to handle the closed timelike line problem for Anti-de Sitter spacetime of any dimension.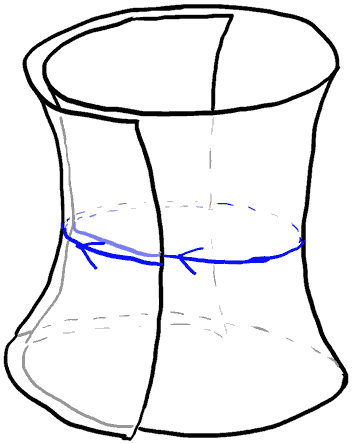

Finally, because time and space are swapped, the spacelike geodesics that were originally parallel but intersected in de Sitter spacetime are now timelike geodesics (those ellipses), which shows that the Anti-de Sitter universe has a tendency to contract, which is exactly the opposite of the expanding universe in de Sitter spacetime.

Introduction to Intrinsic Geometric Curvature

As we have seen, although Minkowski space is the spacetime we are familiar with, many interesting geometries can be derived from it. The “spheres” in Minkowski space, i.e., hyperboloids, can be either pure spaces or spacetimes, and they are all constant curvature spaces. What exactly is curvature?

Extrinsic Curvature

The word “curvature” literally means the degree of bending, i.e., the degree of deviation from linear spaces like straight lines and planes. Indeed, this is what curvature means for a curve. However, for higher-dimensional shapes like planes and hypersurfaces, there are many directions, and the degree of bending is generally different in different directions. Therefore, curvature is no longer a single number, but a complex tensor. For example, the curvature of a plane is 0 in all directions, a cylinder has one zero-curvature direction, and a sphere has the same curvature in all directions. This is the most intuitive geometric concept of curvature. Now, let’s get a little more abstract.

Intrinsic Geometry and Intrinsic Curvature

Consider the state space $M$ of all rotations in three-dimensional space. You can think of each point in this space as representing an orientation state of an object after a rotation. We know that a rotation in three-dimensional space requires a rotation axis and an angle to describe it, so three numbers are needed to describe any rotation, which means that $M$ is a kind of three-dimensional space. In fact, the hypersphere in four-dimensional space can be mapped to space $M$. Since the hypersphere has curvature, this implies that space $M$ also has it. How do we calculate the curvature of space $M$? If we follow the definition of deviation from a plane, our point would run from the hypersphere into four-dimensional space, but for space $M$, the meaningful points are all on the hypersphere, and points in the external space have no meaning. This shows that the meaningful curvature effect should only be related to the “internal distance.” For example, we can define the minimum angle required to rotate from one orientation to another as the definition of distance on $M$. Although it can be proven that this distance is equivalent to the usual hypersphere distance, this inspires us to measure curvature through some geometric effects entirely within the curved space of the hypersphere itself, without relying on the higher-dimensional four-dimensional space. The curvature obtained in this way is called intrinsic curvature.

Let’s go back to the plane, cylinder, and sphere. Assume the plane is made of an inextensible, inelastic paper. We can roll it into a cylinder. During this process, the distance between any two points on the surface of the paper does not change, so the internal geometry does not change, and its curvature is 0. A sphere, on the other hand, has triangles with an angle sum greater than 180 degrees, so it definitely has intrinsic curvature. In fact, many differential geometry textbooks do not assume the existence of an external space. For example, spherical geometry can be fully represented and calculated using two coordinates, latitude and longitude $(x,y)$, but the metric becomes $\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{sin}^2(x)\mathrm{d}y^2$. If you don’t know its connection to a sphere in three-dimensional space, calculating the geodesics directly from the metric would be a very troublesome task! But it must be admitted that this is the general method, because it is not always possible to find a suitable external space that simplifies the calculations.

To intuitively understand the geometric properties of these constant curvature spaces, we have just treated them as if they were placed in a higher-dimensional space like a sphere. However, we need to understand that just like the space $M$ of all three-dimensional rotations, we are only using five-dimensional Minkowski space to construct four-dimensional de Sitter spacetime. The five-dimensional space itself has no physical meaning; only the points on the four-dimensional de Sitter spacetime have physical meaning.

Riemann Curvature Tensor

What geometric effect does intrinsic curvature manifest as? The answer is a rotational effect called holonomy: an object is translated along a closed path and returns to its starting point, but its orientation has changed. The fact that the sum of the angles of a spherical triangle is greater than 180 degrees is also easy to explain: the sum of the angles of a triangle should be 180 degrees, but after a translation along the triangle, it rotates by a larger angle. The tool used to describe this property is the Riemann curvature tensor: imagine an infinitesimally small closed path, which is a parallelogram spanned by two vectors $x$ and $y$. When an object is translated along the loop (assuming it starts along the side corresponding to vector $x$), it will also undergo an infinitesimal rotation. The essence of this rotation is a linear transformation, which maps a given vector $u$ to a vector $v$. The Riemann curvature tensor is a linear transformation that maps $u$ to $v$ for a given $x$ and $y$, i.e., $v=R(x,y)(u)$. The entire tensor is a linear map with three inputs and one output, so its abstract tensor index notation is $R_{abc}^d$.

For isotropic constant curvature spaces, it is much simpler: intuitively, if the rotational effect is in the same direction as the closed path, the curvature is positive. If it is in the opposite direction, the curvature is negative. How do we determine if the rotational effect is in the same direction as the closed path? That’s simple, just look at the picture! The figure below shows the curvature of spherical and hyperbolic geometry, which are clearly positive and negative: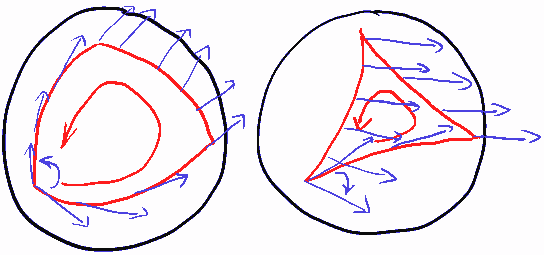

This is true for pure spaces. What about spacetime? Let’s look at two-dimensional de Sitter and Anti-de Sitter spacetime: they are symmetrical, so I haven’t labeled the spacetime axes. From the figures, the curvature should be positive in both cases, but aren’t the curvatures of these two spaces one positive and one negative?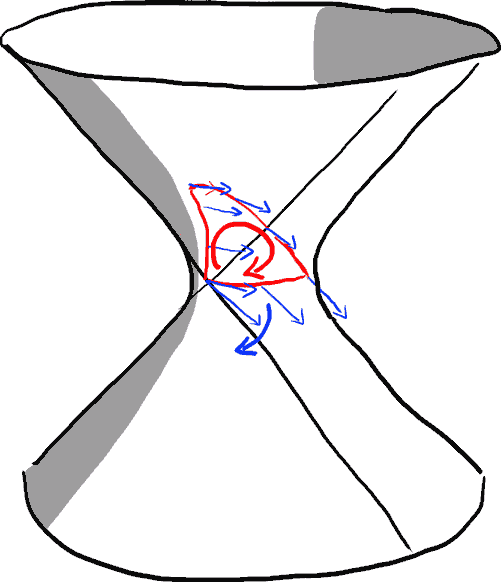

Where is the problem? It must be that the definition of some direction after mixing spacelike and timelike directions is wrong.

1. First, let’s look at the path part: we denote $e_{xy}$ as the directed parallelogram traced along $x\rightarrow y\rightarrow -x\rightarrow -y$. Note that this is actually the 2-vector that was discussed on the blog a long time ago. If we accidentally swap the two sides of the parallelogram, the direction of the path will be reversed, i.e., $e_{xy}=-e_{yx}$. Note that this equation holds regardless of what directions $x$ and $y$ are.
2. Next, let’s look at the rotation part: we denote $e_{x}^y$ as the unit velocity rotation from direction $x$ to direction $y$. The superscripts and subscripts mean that this rotation is a transformation that takes $x$ as input and gives $y$ as output, which means that the velocity direction of a point on the $x$-axis under this rotation is the $y$-axis. Similarly, $e_{y}^x$ is the unit velocity rotation from direction $y$ to direction $x$. If the properties of $x$ and $y$ are the same, it is an ordinary rotation, and these two rotation directions are opposite, with $e_{x}^y=-e_{y}^x$. If the properties of $x$ and $y$ are different, it is actually a hyperbolic rotation, and these two directions are the same, with $e_{x}^y=e_{y}^x$!

A mapping that maps one vector to another can be naturally seen as a mapping that maps a vector and a dual vector to a number. For a vivid explanation, refer to the creative idea Visiting the Infinite Pig Farm. According to the theory of dual spaces, we need to unify the superscripts and subscripts. To pull the superscript down, we must use the metric of the space. Specifically, when the superscript is pulled down, spacelike vectors do not change, but timelike vectors change sign. Here are two examples:

1. For rotation in pure spatial directions, $e_{x}^y=-e_{y}^x$. Changing all indices to subscripts gives $e_{xy}=-e_{yx}$, which is the same antisymmetric formula as the path.
2. Let $x$ be spacelike and $y$ be timelike. Then hyperbolic rotation satisfies $e_{x}^y=e_{y}^x$. Changing all indices to subscripts gives $-e_{xy}=e_{yx}$, which is also the same antisymmetric formula as the path.

This unifies them.

Returning to the curvature calculation. The directions we see in the figure are ordinary 1-vectors $e_x$ and $e_y$, but the rotation actually requires their dual vectors $e^x$ and $e^y$. When we swap the time and space directions of a two-dimensional constant-curvature spacetime, the properties of the vectors used to raise and lower indices also change, resulting in one changing sign and one not.

Does this seem quite complicated? In fact, there is an even simpler way to determine the sign of the curvature (only for these constant curvature spaces, not for general ones). Write down the surface equation, ensuring that the coefficients of the squared spatial terms are positive, and then look directly at the right side of the equation. If it is $1$, the curvature is positive. If it is $-1$, the curvature is negative. (The proof is left as an exercise.) This also explains why negative constant curvature spaces only appear in Minkowski space, because a sphere with a negative radius squared does not exist in Euclidean space, but a “sphere” (hyperboloid) in Minkowski space can have a negative “radius squared.”

Summary of Various Spaces

After talking about so many spaces, let’s list a table to summarize them and end this article:

Space Name	Symbol	Curvature	Property	Construction Method
Euclidean	$\mathbb{R}^n$	0	Pure space	Pythagorean theorem
Minkowski	$\mathbb{R}^{n-1,1}$	0	Spacetime	A different Pythagorean theorem
Spherical	$\mathbb{S}^{n}$	Positive	Pure space	A sphere in $\mathbb{R}^{n+1}$
Hyperbolic	$\mathbb{H}^{n}$	Negative	Pure space	A two-sheet hyperboloid in $\mathbb{R}^{n,1}$
de Sitter	$\mathrm{\mathrm{d}S}^{n}$	Positive	Spacetime	A one-sheet hyperboloid in $\mathbb{R}^{n,1}$
Anti-de Sitter	$\mathrm{a\mathrm{d}S}^{n}$	Negative	Spacetime	A hyperbolic hypersurface in $\mathbb{R}^{n-1,2}$