4D Space (VIII): Visiting a 4D Country
Note: Some content in this article is purely imaginative and contains many loopholes; do not take it seriously.
Celestial Mechanics
We have a relatively comprehensive understanding of 4D geometric bodies. Now imagine one day you are invited to visit a 4D country and learn about their culture and science and technology. What kind of experience would that be?
In the vast 4D universe, galaxies are scattered sporadically. The planet you are going to visit is in one of those galaxies. That planet is a hypersphere, and it also revolves around a star. However, due to an additional dimension, according to “Gauss’s Law,” stellar gravity will decay with the inverse cubic law. You might think this is nothing, but calculations show that this will lead to extremely unstable planetary orbits: they will either crash or fly out of the galaxy.
The planet you are going to is a miracle—its orbit is almost perfectly circular! The civilization on this planet has a history of ten thousand years, and they can only see a few very dim stars in their night sky. This is because if there were nearby celestial bodies, they would disrupt the planet’s circular orbit. For ten thousand years, scientists on this planet could not calculate any deviation from a perfect circle within their precision. However, four thousand years ago, new measurements showed that the planet was deviating from its circular orbit and might leave the star in another thousand years. The scientists later had to correct this tiny orbital difference through several small nuclear explosions. The corrected orbit can sustain the planet for more than another ten thousand years. 
Geography, Transportation, etc.
This world has bustling cities and streets, as well as forests, mountains, and oceans. They have long since drawn world maps, using a double Mercator projection—first projecting the hypersphere onto a spherindrical surface, then projecting it onto a cylindrical surface, and finally unfolding it to obtain a rectangular map. That’s right, all their maps are three-dimensional. On the map, their rivers look like spatial curves with thickness, and lakes are three-dimensional shapes. They never encounter the problem of crossing a river: in three dimensions, you can completely walk around a spatial curve, so unless you’re specifically going fishing in the river, you won’t find a road built on a river. But this doesn’t mean that bridges aren’t needed in mountainous areas: linear ravines carved by riverbeds can indeed be walked around. However, if they encounter lakes, three-dimensional depressions, or two-dimensional fracture planes, bridges must be built. But winding mountain roads and tunnels are unavoidable. I suppose the cross-cell shape of a tunnel should be a sphere.
In cities, traffic congestion is not a problem for them at all. Intersections don’t require overpasses, and main roads with heavy traffic can even be two-dimensional! (Their squares are all three-dimensional.) Of course, their roads are actually 4D; it’s just that height isn’t marked on maps, and road width is ignored, leading to roads being described as one-dimensional or two-dimensional. 
As for the cross-section of a road (not the one cut to expose the foundation), we have no experience whatsoever—our two-dimensional road cross-section is just a line, its length representing the road width. The road I drew above has a circular cross-section, but for a two-way road, this design doesn’t seem very good. I don’t know which cross-section is best, but inferring from the spherical cross-cell shape of tunnels, it’s probably better for the roads inside tunnels to have circular cross-sections.
Note that these abilities, which seem like they can walk freely in three dimensions, do not mean they can fly; they are all “down to earth” on their planet. General rooms in this world are hypercube structures, although designers might build spherindrical or spherindrical rooms… Water pipes are generally sphere-lofted bodies (straight pipes are spherinders). Hopf fibration is their most common form of geometric art, often used to engrave patterns on hyperspherical beads for sale. Their necklaces are made of small, perforated hyperspheres strung together, but another type of spheritorus jewelry is also very popular: using a string to thread together the two-dimensional spherical shells (with thickness, forming a spheritorus) of our three-dimensional spheres. Their clothes are three-dimensional fabrics! They also never weave: a rope in 4D space cannot be knotted, and a perfectly good sweater in our three-dimensional space would turn into a single thread if pulled. Of course, this has advantages: their kite strings will never get tangled. As for vehicles like cars, they can no longer have only 4 wheels, as the car would be unstable, with one side dragging on the ground (imagine your 3D car only having front and rear wheels on the left side, with the right side dragging). So you would see 4D cars with 8 wheels. Of course, we also have simple vehicles like tricycles; for them, if it can stay stable and not fall over, four wheels are essential for a 4D car. Of course, here the shape of the wheels is not a cylinder or a 3D torus; I think they are spherinders or torispheres. But a sphere makes controlling direction a problem, so they might make the front wheels cubinders (or ditorus). Bicycles? Using two spheres or two circles as wheels would probably prevent them from falling, but spherical wheels cannot control the rolling direction, so it’s probably better to use two circular wheels. They still take planes for long distances because, although ground traffic is smooth, turns and friction exist, and there is a maximum speed limit.
Rolling of 4D Objects
Speaking of the rolling of “round” objects in 4D space, the simplest ones are the hypersphere, spherinder, duocylinder, and cubinder.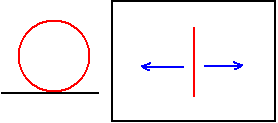
- A cylinder placed flat on a 2D table in 3D space, this placement determines that the rolling direction is unique: perpendicular to its axis of rotation (i.e., its height), which is perpendicular to its intersection line with the tabletop. If forced to move along the intersection line, this is friction and skidding.
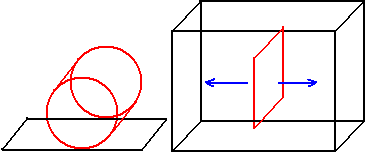
- A cubinder placed flat on a 3D table in 4D space, the rolling direction is also unique: perpendicular to its plane of rotation (it is parallel to its intersection plane with the tabletop). If forced to move along its intersection plane with the tabletop, this is also skidding.
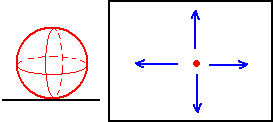
- A spherinder placed flat on a 3D table can roll arbitrarily in the plane perpendicular to its height, just like a sphere rolling on a table.
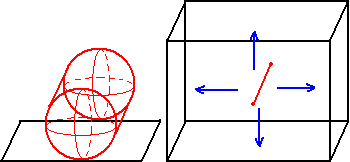
- A hypersphere can roll arbitrarily on a 3D table.
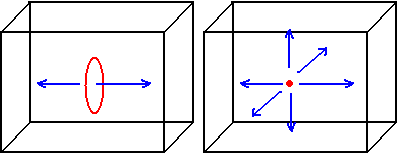
- Although a duocylinder has equal angular rotational symmetry, when placed on a 3D table, only one cell can be tangent to the table (tangent to a circle), causing it to only be able to roll in the direction perpendicular to the tangent circle. In other words, its rolling behaviors are the same as a cubinder, except that the non-rolling side cubinder is square, while the duocylinder is circular. Overall, cubinders and duocylinders can roll in one direction, spherinders can roll freely on a 2D plane, and hyperspheres can roll arbitrarily within a 3D cell.
(Update: A rolling simulator based on 4D rigid body mechanics has been completed, click here!)
In this world, gravity and electromagnetic forces both decay by the inverse cubic law of the distance. So, to cope with the difficulty of overly fast decay, their streetlights are built more densely than ours; but their circuit boards and chips are also three-dimensional, so information technology is very developed. We know that in three-dimensional space, bevel gears are used for power transmission between intersecting axes. Compared to cylindrical gears, they can change the direction of transmission. In 4D space, you just need to add some “thickness” to them: conindrical gears are used for power transmission between intersecting axes. Compared to cubinder gears, they can change the direction of transmission. However, this change in transmission direction is still within a three-dimensional space. How can we design a device that transfers motion in the $xy$ plane to the $zw$ plane? We can use two sets of conindrical gears: the first set is responsible for converting motion in the $xy$ plane to the $xw$ plane, and the second set then converts the $xw$ plane motion to the $zw$ plane. But this method is a bit clumsy; a 4D civilization would surely have invented a one-step transmission part. (I can’t think of it.)
Common Buildings, Items, and Writing
Are the letters of a 4D civilization three-dimensional? If so, are they composed of curved surfaces or spatial curves? I believe that first, they would all choose three-dimensional letters, but different 4D civilizations would have different habits of choosing to use lines or surfaces. For convenience, spatial curves would be the easiest to “write.” However, they would certainly encounter situations where they need to draw lines, surfaces, or cells, and they would need to change pens. Because you certainly wouldn’t want to use a pen for drawing spatial curves to fill an entire three-dimensional cell. So they would have special pens for drawing surfaces (perhaps like brushes), making the work of filling three-dimensional cells much easier (just as we use ordinary pens to color an area). Want to draw straight lines/planes? You would need various dimensional rulers to draw them straight.
A Little Speculation on Electromagnetic Field
Some scientists have discovered the constancy of the speed of light and the theory of relativity, and have also proposed the theory of “five-dimensional spacetime”! In fact, these are largely similar to the properties of our 4D spacetime. But the only exception is their magnetic field: the magnetic field is no longer a vector, but a 2-vector. In the simplest case, if you place a current-carrying wire, you find that the “Ampère force” is maximal when parallel to a certain plane, and there is no force when parallel to a plane absolutely perpendicular to it. Of course, often a 2-vector is not simple, in which case the wire will experience a magnetic force in any orientation! The electromagnetic tensor (which is also a 2-vector) in 4D spacetime corresponding to 3D space looks like this: $$F=\begin{pmatrix} 0 & E_x/c & E_y/c & E_z/c \\ -E_x/c & 0 & -B_z & B_y \\ -E_y/c & B_z & 0 & -B_x \\ -E_z/c & -B_y & B_x & 0 \end{pmatrix}$$I guess the electromagnetic tensor (2-vector) in 5D spacetime corresponding to 4D space looks like this: $$F=\begin{pmatrix} 0 & E_x/c & E_y/c & E_z/c & E_w/c \\ -E_x/c & 0 & B_{xy} & B_{xz} & B_{xw} \\ -E_y/c & -B_{xy} & 0 & B_{yz} & B_{yw} \\ -E_z/c & -B_{xz} & -B_{yz} & 0 & B_{zw} \\ -E_w/c & -B_{xw} & -B_{yw} & -B_{zw} & 0\end{pmatrix}$$
4D World Series
This world is different from the previously discussed geometry or algebra; it includes more settings like physics, so its objectivity and realism are greatly reduced. But the 4D world is wonderful, and I have created a new series independent of the 4D Space Series: 4D World Series to explore this place full of unknowns.