Group Theory Series (2): Field Extensions

With some basic knowledge of groups, we should now discuss the problem of roots of n-degree equations. Before specifically discussing this problem, we need to introduce some new concepts. Many of these concepts are no longer limited to groups and belong to the scope of abstract algebra. This article is somewhat advanced, but it aims to give readers an intuitive understanding of Galois theory, so general conclusions and proofs will be minimized. Interested readers can refer to Wikipedia or abstract algebra textbooks.

Field Extensions

Let’s first look at another algebraic structure similar to groups—fields.
Simply put, a field is a set with four arithmetic operations defined (addition, subtraction, multiplication, and division), while a group only defines multiplication. We won’t give a strict definition, and this article only deals with number fields, where the four arithmetic operations are the ones we normally use, not other definitions.

Apart from finite fields, the smallest number field is the rational field $Q$, because it is closed under division. (The smallest field is the finite field with only two elements {0,1}, but the four arithmetic operations are not our usual definitions, like $1+1=0$, which we won’t discuss here.) When we solve the equation $ax+b=0; a,b\in Q$, all solutions also fall within this field, which is good. But for quadratic equations, like $x^2-2=0$, we know the solution $\sqrt{2}$ is irrational and not in the rational field $Q$. Here, middle school teachers say we extend the number field to get a new number field $R$ that includes all numbers from negative infinity to positive infinity. But this method is crude and suddenly “fills” the real number line. We might first let only $\sqrt{2}$ and rational numbers participate in arithmetic operations, which generates a larger field, denoted as $Q(\sqrt{2})$. Every number in this field can be written in the form $a+b\sqrt{2}; a,b\in Q$. Readers can verify the closure of the four arithmetic operations under this form themselves. We call the operation of adding some elements to a field $k$ to obtain a larger field $K$ a field extension, denoted as $K/k$ (which actually means $k \subseteq K$). Elements in the extension field $a+b\sqrt{2}; a,b\in Q$ can be seen as obtained through two-dimensional linear combinations of the original field. We call dimension two the degree of the extension.

What about the degree of the field extension $Q(\pi)/Q$? Due to the closure of multiplication, $\pi^n$ should all be in the extension field. $\pi$ is different from $\sqrt{2}$; $\pi$ is a transcendental number, so $\pi^n$ cannot be rational. Therefore, numbers $a_0+a_1\pi+a_2\pi^2+..$ must be obtained through infinite-dimensional linear combinations. Note that for the field $Q(\sqrt{2})$, there also seem to be elements $a_0+a_1\sqrt{2}+a_2\sqrt{2}^2+a_3\sqrt{2}^3..$, but once the index is greater than 1, it can be simplified using $\sqrt{2}^2=2$, so these linear combinations are not independent. Although there are infinitely many vectors, there are ultimately only two linearly independent vectors, and the dimension of the corresponding vector space is still 2. Note that if division results in a denominator containing radicals, we can rationalize the denominator, but transcendental numbers containing $\pi$ cannot. This kind of extension containing transcendental numbers leads to infinite-dimensional extensions, which we call infinite extensions, like from $Q$ to $R$ is also an infinite extension, while extensions like $Q(\sqrt{2})$ are called finite extensions. We only care about finite extensions.

Intermediate Extensions

Returning to our concern: we hope that roots of quintic equations have root formulas, which is actually equivalent to saying that roots of quintic equations can fall within a field obtained after a field extension with a given structure. Before describing these extensions, let’s look at some simple examples:

The field $K=Q(\sqrt{2},\sqrt{3})$ generated by adding $\sqrt{2}$ and $\sqrt{3}$ can be proven to have all elements writable in the form $a+b\sqrt{2}+c\sqrt{3}+d\sqrt{6}$. We find that $E_1=Q(\sqrt{2})$, $E_2=Q(\sqrt{3})$, and $E_3=Q(\sqrt{6})$ are all subfields of this field. Since these fields are all extensions of $Q$, $E_1, E_2, E_3$ are intermediate fields between fields $Q$ and $K$. Intermediate fields represent the structure of field extensions in a certain sense. So given a field extension, what general method do we have to find intermediate extensions?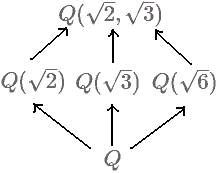

The answer is: use group theory!!

Automorphism Groups of Field Extensions (Galois Groups)

The reason we can use group theory to study the problem of roots of quintic equations is that studying field extensions can be transformed into studying automorphism groups of field extensions. What is an automorphism group of a field extension? Simply put, we define some automorphism mappings, and they form a group through composition operations. An automorphism mapping $f$ of a field extension $K/k$ is defined as:

• A bijection from $K$ to itself (a permutation operation on elements in $K$, see the previous article);
• Preserves the field structure, meaning the four arithmetic operations on the field. For example, $f(a)+f(b)=f(a+b)$, $f(a)f(b)=f(ab)$, etc.;
• Additional requirement (otherwise it’s no different from general field automorphism groups): the permutation operation must keep the original field $k$ unchanged, i.e., for all $a\in k$, we have $f(a)=a$.

In honor of mathematician Galois, we call the automorphism group of a field extension $K/k$ satisfying certain conditions (we’ll ignore the conditions for now) the Galois group, denoted as $Gal(K/k)$.

The definition is somewhat abstract, so let’s look at several examples (the following examples are all from Wikipedia): The simplest example, find $Gal(Q(\sqrt{2})/Q)$: First, we need to find the automorphism mapping $f:Q(\sqrt{2})\rightarrow Q(\sqrt{2})$. Note that we can’t just assign different elements to each element in $Q(\sqrt{2})$, because by definition the permutation operation must keep the original field $k$ unchanged and preserve the structure of the original field: we have $\sqrt{2}^2=2$, so we must have $f(\sqrt{2})^2=f(\sqrt{2}^2)=f(2)=2$, solving this gives $f(\sqrt{2})$ can be $\pm\sqrt{2}$. This corresponds to two automorphism mappings, where $f_1(\sqrt{2})=\sqrt{2}$ is the identity mapping, and $f_2(\sqrt{2})=-\sqrt{2}$ maps $a+b\sqrt{2}$ to $a-b\sqrt{2}$. They form a group isomorphic to $S_2$ through composition operations, i.e., $Gal(Q(\sqrt{2})/Q)=S_2$.

Let’s try a slightly more complex one: $Q(\sqrt{2},\sqrt{3})$. With the experience from last time, we can quickly give four mappings (the key is using $\sqrt{x}^{2}=x,x\in Q$):

• $e$: $e(\sqrt{2})=\sqrt{2}$, $e(\sqrt{3})=\sqrt{3}$ (i.e., identity mapping)
• $a$: $a(\sqrt{2})=-\sqrt{2}$, $a(\sqrt{3})=\sqrt{3}$
• $b$: $b(\sqrt{3})=-\sqrt{3}$, $b(\sqrt{2})=\sqrt{2}$
• $ab$: $ab(\sqrt{2})=-\sqrt{2}$, $ab(\sqrt{3})=-\sqrt{3}$

It can be proven that these are all the automorphism mappings. We see that these four elements form a group. The characteristic of this group is that all elements are of order two, and the product of any two non-identity elements equals another non-identity element (for example, $ab*a=b$), and it is an abelian group. It’s called the Klein four-group.

Subgroups and Intermediate Extensions

Let’s now see what connections exist between automorphism groups corresponding to different intermediate extensions. There are two possible approaches:

• Bottom-up extension: Taking the smallest field $Q$ as the baseline, consider the relationship between groups $Gal(Q(\sqrt{2},\sqrt{3})/Q)$, $Gal(Q(\sqrt{2})/Q)$, $Gal(Q(\sqrt{3})/Q)$, $Gal(Q/Q)$;
• Top-down extension: Taking the largest field $Q(\sqrt{2},\sqrt{3})$ as the baseline, consider the relationship between groups $Gal(Q(\sqrt{2},\sqrt{3})/Q(\sqrt{2},\sqrt{3}))$, $Gal(Q(\sqrt{2},\sqrt{3})/Q(\sqrt{2}))$, $Gal(Q(\sqrt{2},\sqrt{3})/Q(\sqrt{3}))$, $Gal(Q(\sqrt{2},\sqrt{3})/Q)$.

Since bottom-up extension always takes the smallest field $Q$ as the baseline, when we study $Gal(Q/Q)$, it has nothing to do with $\sqrt{2}$ or $\sqrt{3}$, and we cannot connect them as a whole. So we choose to consider top-down extension, taking the largest field $Q(\sqrt{2},\sqrt{3})$ as the baseline.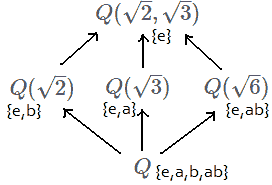

The diagram shows elements of the Galois group $Gal(Q(\sqrt{2},\sqrt{3})/K)$ next to each field $K$. We see that the Galois group corresponding to a field is a subgroup of the Galois group corresponding to its subfield! This is the Fundamental Theorem of Galois Theory. This makes sense: the Galois group consists of mappings that keep the original field unchanged, so when the original field expands, the mappings decrease, forming a subgroup of the original group. For example, from $Q$ to $Q(\sqrt{2},\sqrt{3})$ we could originally operate on $\sqrt{2}$ and $\sqrt{3}$, but in the Galois group from $Q(\sqrt{2})$ to $Q(\sqrt{2},\sqrt{3})$, we can no longer operate on $\sqrt{2}$, so only {e,b} operations remain.

Galois Extensions

Let’s look at the extension $Q(\sqrt[3]{2})/Q$. Since $(\sqrt[3]{2})^3=2$, we require the mapping $f$ to satisfy $f(\sqrt[3]{2})=2$, but this equation has two other roots that are complex and won’t appear in the extension field $Q(\sqrt[3]{2})$. This results in only the identity mapping satisfying the requirements, and the Galois group is the trivial group {e}. It feels like the Galois group doesn’t reflect the cubic structure of the extension $Q(\sqrt[3]{2})/Q$ as we expected. This is what we skipped earlier: Only automorphism groups of field extensions satisfying certain conditions are called Galois groups: We shouldn’t consider fields extended by adding arbitrary numbers, but should consider those that add exactly all roots of a polynomial equation (with polynomial coefficients all rational). (This kind of field obtained by adding exactly all roots of a polynomial equation is called a splitting field, because we can completely factor the polynomial in the extension field.) We call extensions satisfying the above conditions normal extensions, also called Galois extensions (Note: Fortunately we only study number fields, otherwise normal extensions wouldn’t be equivalent to Galois extensions and would require the condition of separable extensions.) It can be proven that only Galois extensions allow a one-to-one correspondence between field extensions and subgroups.

Going back, since $\sqrt[3]{2}$ is a root of the equation $x^3=2$, this equation has two other roots $\sqrt[3]{2}\omega$ and $\sqrt[3]{2}\omega^{2}$ (where $\omega=1/2+i\sqrt{3}/2, \omega^{3}=1$). So we’d better consider changing the problem to finding the extension of the field $Q(\sqrt[3]{2}, \sqrt[3]{2}\omega, \sqrt[3]{2}\omega^{2})$ over $Q$. Only such extensions are “profitable”.

For brevity, let $\sqrt[3]{2}=\theta$. Below we write the equations connecting $\theta$, $\omega$, and $Q$:

$\theta^{3}=2$     The solutions of the first equation are $\theta$, $\theta\omega$, $\theta\omega^{2}$, $\omega^{3}=1$     The solutions of the second equation are $1$, $\omega$, $\omega^{2}$.

Our automorphism mappings are permutations of these roots… but note that $1$ is rational, so we must preserve it and cannot permute $1$. So the results of automorphism mappings acting on $\theta$ have three possibilities: $\theta$, $\theta\omega$, or $\theta\omega^{2}$, while acting on $\omega$ can only have two results: $\omega$ or $\omega^{2}$. This shows that $Gal(Q(\sqrt[3]{2})/Q)$ has six elements, which can be represented as {e, f, f², g, gf, gf²}. Where:
$$f(\theta) = \omega\theta, ; f(\omega) = \omega, \quad g(\theta) = \theta, ; g(\omega) = \omega^2. $$Note this group is not abelian, because $fg = gf^2$.

Let’s draw the Cayley diagram of this group:

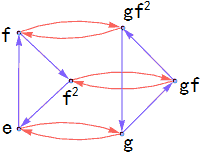
Look familiar? It’s isomorphic to the symmetric group $S_3$ we studied before: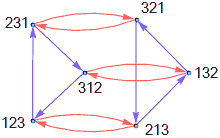
We also discussed the non-trivial subgroups and cosets of group $S_3$ in the previous article. Here’s the result again: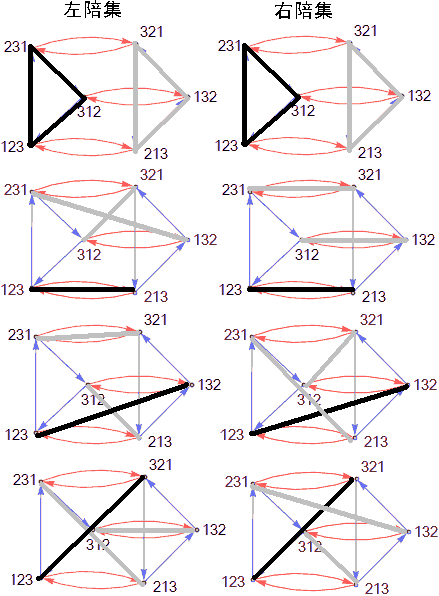
The correspondence between these non-trivial subgroups and intermediate fields is:
Note that the trivial subgroup {e} corresponds to the trivial extension, and the trivial subgroup {e, f, f², g, gf, gf²} corresponds to the entire extension, which is also not an intermediate extension (we also consider it a trivial intermediate extension). It seems trivial subgroups exactly correspond to trivial extensions.

Earlier we called extensions that contain exactly all roots of a polynomial normal extensions. Is it called “normal” because it corresponds to normal subgroups? The answer is yes! For example, {e, f, f²} corresponds to the normal extension $Q(\omega)/Q$. There’s a theorem:

Given field extensions $k\subset K\subset E$, where $K/k$ and $E/k$ are both normal extensions, then $Gal(E/K)$ is a normal subgroup of $Gal(E/k)$, and $$Gal(E/k)/Gal(E/K)\cong Gal(K/k)$$

Wait! We’ve discussed so much now, what does this have to do with the radical representation of roots of n-degree equations that we originally wanted to study? Let’s put aside the proof of the above theorem and see how to use the language of field extensions to describe “n-degree equations have radical representations for their solutions”.

Radical Towers

First, saying a number can be represented using finite arithmetic operations and non-nested square roots is actually equivalent to saying there must exist a number field $K_1=Q(\sqrt{u_1},\sqrt{u_2},..,\sqrt{u_n}), (u_1, .., u_n \in Q)$ such that this number falls within it.

Saying a number can be represented using finite arithmetic operations and square roots implicitly allows us to nest square roots, like:
$${\sqrt{\sqrt{2}+5}\over 1+\sqrt{\sqrt{\sqrt{3}-2}+\sqrt{7}}}$$ How do we construct the extension field in this case? The answer is: construct it layer by layer. For example, we first obtain the field $K_1$ containing only one layer of radicals, then we do another layer of radical extension on its basis to get $K_2=K_1(\sqrt{u_1},\sqrt{u_2},..,\sqrt{u_n}), (u_1, .., u_n \in K_1)$. $K_2$ represents numbers that can be expressed with two layers of square roots. This method of describing radical nesting through layer-by-layer extensions $Q\subset K_1\subset K_2 …\subset K_n$ is called a radical tower.

That solutions of n-degree equations have radical representations means the solutions can be expressed using the coefficients with finite arithmetic operations and radicals. Assuming the coefficient field is k, this is equivalent to the solutions falling within the field tower
$k\subset K_1\subset K_2 …\subset K_n$, where $K_{i+1} = K_i(u_i), u_i^{n}\in K_i, n\in Z$. Note we only add one element at a time, like $\sqrt{2}+\sqrt{3}$ is considered as two extensions. This view doesn’t affect the result. We can even require the degree n to be prime, because a composite root of a number can be expressed as nested roots of the prime factors of the composite.

Now let’s look at the Galois group of the largest field extension $K_n/k$: Of course, when the field extension adds root $u_j$, we need to add all solutions of $u^{n}=a, a\in K_i$ to make all extensions normal (this doesn’t affect whether the numbers we want fall within or whether other unwanted numbers fall within). According to the previous theorem, the normality of the field tower corresponds to the normality of subgroups. If a field extension’s corresponding Galois group cannot find a series of normal subgroups with the corresponding structure, then this field extension definitely isn’t a radical extension, meaning numbers in this extension cannot be expressed using finite arithmetic operations and radicals.

Galois Groups of Radical Extensions

Now let’s handle some details, like what structure exactly do we need for a series of normal subgroups with the corresponding structure? Let’s first look at the Galois group of a one-layer radical extension: $Gal(k(u)/k),u^n\in k$.

According to the fundamental theorem of algebra, the equation $u^n=a, a\in k, a\neq 0$ must have n roots, which are respectively $$\left\lbrace u,u\omega,…,u\omega^{n-1}\right\rbrace , \omega=exp(2\pi i/n), \omega^n=1$$We need to consider two cases: $u\in k$ and $u\not\in k$.

• $u\in k$: This case means we can extract the nth root within the number field $k$, so $u$ cannot participate in permutations, and we can only permute the other roots. If n is prime, we can prove that all mappings $f_a(u\omega)=u\omega^a , a < n$ form a cyclic group $C_{n-1}$: because we can easily verify $f_a f_b (u\omega)= f_b f_a (u\omega) = u\omega^{a+b} = f_{a+b} (u\omega)$. (A noteworthy detail is: if n is composite, the composition of these mappings might map $u\omega^a$ to $u\omega^n=1$, which we don’t want. For example, when n=4, $f_2(u\omega^2)=u\omega^4=u$, which doesn’t meet the requirement that the mapping fixes $u$.)
  For example, if we take $u=1$, it represents the extension adding all nth roots of unity $\omega,..,\omega^{n-1}$.
• $u\not\in k$: This case means all roots can be permuted, but here we first assume the roots of unity $\omega,..,\omega^{n-1}$ have already been added to field k, so we won’t do mappings that permute $\omega^n$ but keep u unchanged, only do mappings between $u,u\omega,..,u\omega^{n-1}$. Similarly, we can prove they form the cyclic group $C_{n}$.

To summarize: Given a radical tower, we first decompose all radicals into nested prime power radicals, then add all nth roots of unity needed for the radicals, then add radicals layer by layer to get the final radical tower. According to the previous analysis, the Galois group of each field extension step in the radical tower (they are all normal extensions) is a cyclic group.

Now we should use the theorem about normal subgroups and normal extensions that we haven’t proven yet:

Given field extensions $k\subset K\subset E$, where $K/k$ and $E/k$ are both normal extensions, then $Gal(E/K)$ is a normal subgroup of $Gal(E/k)$, and $$Gal(E/k)/Gal(E/K)\cong Gal(K/k)$$

(Proving this theorem requires the First Isomorphism Theorem for groups [+]Show details)

A group is a set plus an operation. There can be mappings between sets. We call mappings $f$ that **preserve group structure** group homomorphisms, i.e., preserve group operations $f(a)*f(b)=f(a*b)$. It's easy to verify that if some elements of group A are mapped to the identity element of group B, then these elements form a subgroup in group A, which we call the **kernel** of the mapping. It's also not hard to verify that all elements in a coset of A will be mapped together to one element in B. Since B is also a group, this conversely shows that multiplication between cosets in A can be well-defined, i.e., the **kernel** of the mapping is always a **normal subgroup** of A. And the image of the mapping (a subgroup in group B) is isomorphic to the quotient group A modulo the kernel. This is the **First Isomorphism Theorem for groups**.

First, we know $Gal(E/K)$ is a subgroup of $Gal(E/k)$, because the automorphisms of the former are just part of the latter. So if we can define a homomorphic mapping between the two automorphisms, the problem is solved. If the extension is normal, we can find such a homomorphic mapping (roughly restricting the action of mappings in the large automorphism group to the small automorphism group). See relevant books for details.

Let’s apply this theorem to the radical tower: $k\subset K_1\subset ..\subset K_{i}\subset E$

$$Gal(E/K_1)/Gal(E/K_{2})\cong Gal(K_{2}/K_1)\\
Gal(E/K_2)/Gal(E/K_{3})\cong Gal(K_{3}/K_{2})\\
…\\
Gal(E/K_{i-1})/Gal(E/K_{i})\cong Gal(K_{i}/K_{i-1})\\
Gal(E/K_{i})/Gal(E/E)\cong Gal(E/K_{i})$$

This shows that $Gal(E/K_{2})$ is a normal subgroup of $Gal(E/K_1)$, $Gal(E/K_{3})$ is a normal subgroup of $Gal(E/K_{2})$, …, $Gal(E/E)=${e} is a normal subgroup of $Gal(E/K_i)$. We get a conclusion: $Gal(E/K_1)$ must have a normal subgroup of a normal subgroup of… of a normal subgroup, finally getting the trivial group {e}, and of course the quotient groups corresponding to these normal subgroups must all be cyclic groups. We call groups with this structure solvable groups, which means the Galois group of an extension obtained by adding numbers that can be expressed using arithmetic operations plus radicals must be a solvable group. If not, it means the numbers we added cannot be expressed using arithmetic operations plus radicals.

Finally, let’s look at the Galois group of the field extension obtained by adding all roots of a quintic equation: For group element f,
$$f(x^5+a_4 x^4+..+a_0)=f(0)=0\\
f(x)^5+a_4 f(x)^4+..+a_0=0$$
The most general case for this equation is 5 different irrational roots. For example, the Galois group of the field extension adding all roots of equation $x^5-4x+2=0$: it can at most permute all roots, so it’s a subgroup of group $S_5$, but it’s easy to verify that equation $x^5-4x+2=0$ has two conjugate complex roots, meaning we can at least exchange these two roots, i.e., it contains group elements of order two. Actually, the number of elements in the Galois group of all quintic equations without rational roots must be a multiple of five (because numbers in the number field after adding each root $z$ can be uniquely written in the form $a+bz+cz^2+dz^3+ez^4$ [+]Why?, indicating the existence of a degree-five extension.), and the only subgroup satisfying both conditions above is $S_5$ itself (we will analyze the structure of $S_5$ in the next article).

First, numbers in the number field can all be written as $a+bz+cz^2+dz^3+ez^4$, because according to the equation, $z^5$ can be expressed by the previous form. The closure under division is not obvious, but we can use the method of undetermined coefficients to find that the inverse of every number of the form $a+bz+cz^2+dz^3+ez^4$ can also be written in this form $a'+b'z+c'z^2+d'z^3+e'z^4$. From the equation $(a'+b'z+c'z^2+d'z^3+e'z^4)(a+bz+cz^2+dz^3+ez^4)=1$, by equating corresponding coefficients, we get a system of equations that can be verified to have solutions in general cases. Now for uniqueness: if not unique, it means root $z$ is also a solution of some rational coefficient equation $a+bz+cz^2+dz^3+z^4=0$. We completely factor the polynomials $x^5-4x+2$ and $a+bz+cz^2+dz^3+z^4$ over the largest complex field, then divide to cancel the common root $z$ to get a fraction. The remaining numerator and denominator are irreducible irrational factors. Since the numerator and denominator were originally rational coefficient polynomials, after canceling the irrational factor $(x-z)$, the coefficients must be irrational. But the quotient of two rational polynomials must have rational coefficients, which is a contradiction. (Note this is not rigorous; see relevant books for proof.)

We will prove that group $S_5$ is not solvable, i.e., there doesn’t exist the series of normal subgroups described earlier. Here we have successfully transformed the problem completely into a group theory problem. Because any extension field corresponding to an automorphism group that contains adding a root $z$ must be able to exchange $z$ with the other four roots, meaning this group contains at least $S_5$. But since $S_5$ is not solvable, all larger groups containing $S_5$ will also not be solvable.

We will analyze why there is no corresponding series of normal subgroups in $S_5$ through conjugacy classes. (To be continued)

/***
　　Note, this article only aims to present readers with a general outline of Galois theory, and there are many details I haven't clarified
　　For more details, see "A First Course in Abstract Algebra"
***/