Group Theory Series (Part 1): Introduction to Group Theory

Why do quintic equations have no radical solutions? Galois provided a perfect answer using group theory. For the history and introduction of group theory, I highly recommend this article “Finite Simple Groups: A Century-Long Journey“.
But what specific knowledge do we need to understand Galois theory? Most engineering students haven’t studied group theory or abstract algebra. I plan to write a series of articles, hoping to explain everything starting from zero foundation. Our main thread is understanding Galois theory, though groups have many other applications in mathematics, physics, and chemistry, and I’ll cover some of these other applications.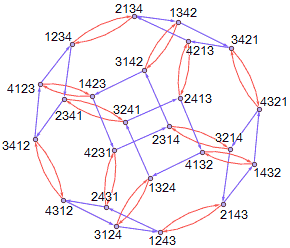

Table of Contents

• What is a Group?
• Cyclic Groups
• Subgroups
• Cosets and Lagrange’s Theorem
• Symmetric Groups
• Quotient Groups
• Alternating Groups
• Simple Groups

What is a Group?

If you’re already familiar with the concept of groups, you can skip this section. Simply put, a group is a set G equipped with a multiplication operation that satisfies certain requirements. These requirements are called the “group axioms“:
Let a, b, and c be arbitrary elements of G. Then:

1. Closure. a*b is in G;
2. Associativity. (a*b)*c = a*(b*c);
3. Identity element. There exists an identity element e in G such that a*e = e*a = a. The identity element e of G can be proven to be unique;
4. Inverse element. For each a in G, there exists an inverse x in G such that a*x = x*a = e. The inverse x of a can be proven to be unique.

The multiplication operation mentioned in the definition is not actual multiplication, but rather an operation satisfying certain requirements. I think calling it a “composition operation” would be less misleading than multiplication. We just denote it as *: a*b represents doing operation b first, then operation a. (The right-to-left notation is just to be consistent with the convention for composite functions $f*g(x)=f(g(x))$)
Show detailed explanation of these four axioms using addition as an example

1. First, each element in a group's set is an "operation", and any two elements can be multiplied to get another element in the set, i.e., the composition of two operations. For example, integers with integer addition form a group, where element n represents the operation +n, and the composition of elements n and m is the operation +n+m = +(n+m), corresponding to element n+m.
2. (a\*b)\*c = a\*(b\*c) because both sides represent the composite operation "first c, then b, then a".
3. Groups also require an "identity element", i.e., "no operation", like adding 0. This operation composed with any operation a is still operation a.
4. The multiplication operation in groups defined this way seems too broad - it seems all operations could satisfy it. So we require that each operation can find a corresponding "inverse operation" in the group, such that the composition of these two operations is the identity element "no operation". For example, in addition, the inverse of +n is -n, and their composition is adding 0. So integers with integer addition satisfy the group requirements, but natural numbers with addition don't work, because the inverse of adding a natural number is a negative number, which isn't in the natural number set.

Note: The group axioms do not require multiplication to be commutative, meaning two operations in different orders are different. For example, matrix multiplication and geometric rotations and translations: imagine a person walking forward one meter then turning left 90°, versus turning left 90° then walking forward one meter - the final results are different.

Some Examples

Groups aren't meant for checking which number sets with arithmetic operations satisfy the axioms, but for studying sets of operations with common forms and their properties. For instance, in a symmetric figure, we put all transformations that keep the figure unchanged into a set. These transformations reflect the figure's symmetry and form a group called the figure's symmetry group. For example, there are 8 operations that keep a square unchanged, forming group $D_8$.Show the specific 8 operations

1. No operation
2. Rotate 90° clockwise
3. Rotate 180° clockwise
4. Rotate 270° clockwise
5. Vertical flip
6. Horizontal flip
7. Diagonal flip
8. Other diagonal flip

What’s the use of knowing this? Actually, we don’t care about these operations themselves, but about the overall structure of their composition operations. For example, group $A=\lbrace ×1 operation, ×-1 operation\rbrace$ and group $B=\lbrace no figure operation, horizontal flip figure\rbrace$ describe completely different operations, but they have the same structure: both have an identity element, and the other operation composed with itself equals the identity. We say these two groups are the same in the sense of isomorphism. Isomorphism means there’s a one-to-one correspondence between elements of two groups, and the multiplication results also correspond one-to-one. This allows us to study group theory abstractly. The group described above is called the cyclic group of order 2, denoted $C_2$. We say the order of a group is the number of elements in the group. Now let’s look at some abstract group examples:

Cyclic Groups

Let’s first intuitively explain the cyclic group of order n: the group generated by the operation “rotate 1/n of a full turn”. Here “generated” means the smallest group containing the given operation. Due to closure under multiplication in groups, we can deduce that operations “rotate k/n of a full turn” (k from 0 to n-1) should all be in the group. We can verify that this set of operations already satisfies all group axioms, so this is the group generated by the operation “rotate 1/n of a full turn”. We label the operation “rotate k/n of a full turn” as k.
The rigorous definition of a cyclic group of order n is a group $G$ where there exists an element $g$ such that every element in $G$ is of the form $g^k$ ($k\in Z$). Here, the power of an element represents composing it with itself k times.
In the sense of “isomorphism“, cyclic groups can also be viewed as “the additive group of congruence classes modulo n”, which sounds complicated but is actually just the set {0,1,…,n-1} with addition defined as: if the sum of two numbers exceeds n-1, take the remainder when divided by n to ensure the result stays in the set (closure). Note that multiplication in this group satisfies commutativity (because the defined addition operation naturally has commutativity), making it a commutative group (also called an abelian group).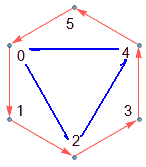

Subgroups

Looking carefully, we notice that taking three elements {0,2,4} from group $C_6$, they also satisfy the group axioms, meaning this is a subgroup of $C_6$, similar to a subset. The group {0,2,4} is isomorphic to $C_3$ (the blue triangle), and actually {0,3} is also a subgroup, isomorphic to $C_2$. Note that the set containing only the identity element {0} and the whole set {0,1,2,3,4,5} are also subgroups, but these two cases aren’t interesting, so we call them trivial subgroups. Doesn’t this look like how any number can be divided by 1 and itself? This way we can define a concept similar to prime numbers… Let’s pause here and return to the discussion of subgroups. There is indeed a concept similar to prime numbers - simple groups, but its definition isn’t like this. We’ll discuss it after covering normal subgroups.
Are there other subgroups? We could search slowly, but Lagrange’s theorem tells us that the order of a subgroup must divide the order of the original group (order of group = number of elements in group), meaning subgroups of $C_6$ can only have order 1 ({0}), 2, 3, or 6 (itself). This greatly reduces our search range. We find there’s only one subgroup each of order 2 and 3, which are {0,3} and {0,2,4} respectively. Thus, $C_6$ has 4 subgroups total.

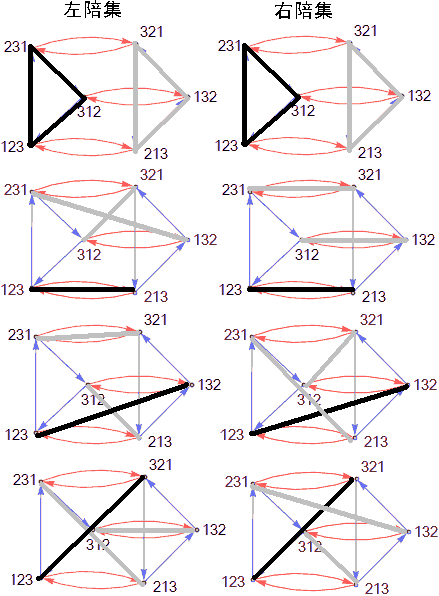
Cosets and Lagrange’s Theorem

Subgroups have much stronger requirements than subsets because subgroups require internal closure under multiplication. If group G has subgroup H, any element g of group G can be multiplied with all elements of subgroup H (if not a commutative group, then consistently left multiply or right multiply), and the results form a new set called a coset, denoted gH or Hg (left multiplication gives left cosets, right multiplication gives right cosets).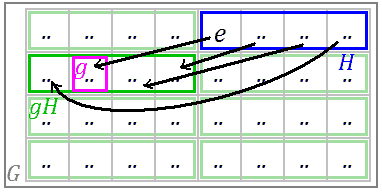

Different cosets don’t intersect. Taking left cosets as an example, we have two cases:

• If g is already an element in subgroup H, due to closure, the results are also in subgroup H, and all results exactly form set H. If it’s not exactly set H, it means g multiplied by two different elements in H gives the same result, which contradicts the uniqueness of inverses in groups.
• If g is not an element in subgroup H, the resulting set has the same number of elements as the order of subgroup H (again due to uniqueness of inverses), and two different elements’ corresponding cosets g1H, g2H are either equal or have empty intersection.
  Show proof Suppose left cosets (right cosets similarly) $g_1H$, $g_2H$ intersect, i.e., there exist $h_1, h_2\in H$ such that $g_1h_1=g_2h_2=c$, then $g_1=g_2h_2h_1^{-1}$, so for any $h$, we have $g_1h=g_2h_2h_1^{-1}h$, thus $g_1H\subseteq g_2H$. Similarly $g_2H\subseteq g_1H$, so the two sets are equal.

This shows that these cosets are pairwise disjoint, and all elements in G are in some coset - G can be decomposed as a union of left (or right) cosets, and the number of elements in a coset equals the order of subgroup H, so the order of H divides the order of G. The quotient from division, i.e., the number of left cosets and right cosets are equal, called the index of H in G.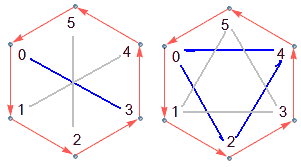

In the figure above, the subgroup of order 2 on the left has three cosets (remember the subgroup itself is also a coset), the subgroup of order 3 on the right has two cosets, and the whole group has order 6.

Symmetric Group $S_3$

Before we discuss the next abstract concept, let’s look at some other groups. Note that the symmetric group here is different from the symmetry group of geometric figures: the symmetric group $S_n$ refers to the set of all bijections from the set {1,2,…,n} to itself, or in plain terms, all permutations of {1,2,…,n} representing permutation operations. Let’s look at the example $S_3$:
The permutations of {1,2,3} number 3! = 6, namely: 123, 132, 213, 231, 312, 321.
Here 123 is “no operation”, 132 is “swap the second and third numbers”, which we abbreviate as “2->3,3->2”, 213 is “2->1 1->2”, etc.
We take two special operations a=213 (swap 1 and 2), b=231 (cycle), and can draw a diagram to represent the composition relationships between these 6 element operations: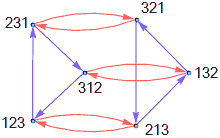

Blue arrows represent operation b=231, red represents a=213. We find that other elements can all be expressed as products of these two elements and their inverses, showing that a and b are generators of $S_3$. This method of representing groups by drawing generators as arrows is called a Cayley graph. The cyclic group diagrams we saw earlier are also Cayley graphs.
How many non-trivial subgroups can you find? Can you draw their cosets?
Show answer



Note that this group is not commutative, because changing the order of these permutation operations gives different results. In fact, $S_3$ is the smallest non-commutative group. When finding its subgroups, Lagrange’s theorem tells us that non-trivial subgroups must have order 2 or 3. Since subgroups must contain the identity element, do we still need to try 5 + 5*4 possible cases? Are there techniques for quickly finding subgroups? First, we mark the order of each group element - this is a concept unrelated to the order of the group - the order of element g is the smallest positive integer k such that $g^k=e$. If no $g^k=e$ can be found except k=0, we define the order of element g as infinity. Of course, in finite groups all elements have finite order, otherwise due to closure under multiplication, $\lbrace g^0, g^1 , g^2.. g^\infty \rbrace$ would all be in the set. In $S_3$ there are 2 elements of order 3 (231, 312), 3 elements of order 2 (213, 132, 321), and one element of order 1 (123). Here we use a corollary of Lagrange’s theorem: the order of every element divides the order of the group. This is because an element of order n generates a cyclic subgroup of order n in the group, and the order n of the subgroup must divide the order of the group. We find that each element of order 2 generates a cyclic group $C_2$ (3 total), and the 2 elements of order 3 generate the same subgroup $C_3$. If a subgroup contains both elements of order 2 and 3, then the subgroup has order 6, which is the trivial group. So all non-trivial subgroups of $S_3$ are just these 4.
Note that symmetric group $S_2$ and cyclic group $C_2$ are equivalent, so a group can have many different interpretations. (In the sense of isomorphism)

More Complex Symmetric Groups

We see that the Cayley graph of $S_3$ is a triangular prism. Below, the Cayley graph of $S_4$ is actually a stereographic projection of a semiregular polyhedron! This semiregular polyhedron is called the rhombicuboctahedron, obtained by cutting edges and vertices from a cube. The eight blue triangles correspond to the 8 vertices cut from the cube, the 6 red squares correspond to what remains of the original 6 faces after cutting… (As someone who loves regular polytopes, I can’t help saying a bit more)

Of course, the choice of generators isn’t unique, so we can get different-looking Cayley graphs that all represent the same group. Hard to imagine, right?

This is a ? truncated octahedron.
The next symmetric group - $S_5$ has order $5!=120$. This group is too large, and the Cayley graph doesn’t look good. Mathematica draws it as a tangled mess. This group plays an important role in proving why quintic equations have no radical solutions, but we won’t discuss that here yet.

Quotient Groups

Let’s focus on cosets again. The number of elements in each coset is the same as the number of elements in the subgroup, which makes cosets feel like copies of the subgroup. One way to think about it is that cosets are the action of elements of group G on subgroup H. This action is also called “translation” - element g acts on subgroup H, “translating” set H to gH. Can we treat cosets as wholes and define multiplication between two cosets so that all cosets form a group? The answer is yes, as long as all left and right cosets of a subgroup H are equal, our wish can be realized. This new group is called a quotient group, denoted $G/H$. A simple intuitive explanation of multiplication between cosets: pick a “representative” element from each of two cosets and multiply them. The result will fall in a new coset, and this new coset is defined as the result of multiplying the two cosets.

Why do we create the concept of “quotient groups”? Wikipedia’s reasoning comes from integer division. When dividing 12 by 3 to get 4, it’s because we can regroup 12 objects into 4 subsets each containing 3 objects. Quotient groups follow the same idea, but use a group as the final answer rather than a number, because groups have more structure than random sets of objects.

Not every subgroup is a “factor” of the whole group (like integer divisors) - only subgroups with equal left and right cosets are. We call these normal subgroups, denoted $H\lhd G$.
Show specific definition of quotient groups

If set $N$ is a normal subgroup of $G$, then:
We define set $G/N$ as the set of all left cosets of $N$ in $G$, that is $G/N = \lbrace aN : a\in G \rbrace$. For each $aN$ and $bN$ in $G/N$, the product of $aN$ and $bN$ is $(aN)(bN)$. This operation is closed, because $(aN)(bN)$ is actually a left coset:
$(aN)(bN) = a(Nb)N = a(bN)N =(ab)NN =(ab)N$.
Note: The equality of left and right cosets of N was used in this equation.

Examples of Quotient Groups

Addition on the set of integers forms group $Z$, and addition of all even numbers also forms a group, denoted $2Z$, which is a subgroup of $Z$. We easily find that this subgroup has two cosets: {all odd numbers, all even numbers}. Since even+even=even, even+odd=odd+even=odd, odd+odd=even, this shows that operations between cosets form a group, and it’s isomorphic to cyclic group $C_2$ (or symmetric group $S_2$), i.e., cyclic group $C_2=Z/2Z$.[Show]Why isomorphic?

It’s isomorphic to the cyclic group because: even corresponds to no operation (or +0 operation), odd corresponds to half rotation (or +1 then take remainder when divided by 2); it’s isomorphic to the symmetric group because: even corresponds to no operation (12), odd corresponds to swap (21).
Actually, this can be generalized to all cyclic groups, with $C_n=Z/nZ$.
Let’s look at examples on finite groups: Since cyclic groups are commutative, all subgroups are normal (left and right cosets are equal), we have $C_{mn}/C_m=C_n$.

Alternating Groups

The alternating group is a subgroup of symmetric group $S_n$, denoted $A_n$. It’s the group formed by all even permutations in $S_n$. The parity of a permutation refers to decomposing the permutation into a composition of multiple transpositions (i.e., swapping only two numbers at a time). It can be proven that for a given permutation, regardless of the decomposition method, the parity of the final number of transpositions remains unchanged. Thus all even permutations form a subgroup, and all odd permutations form a coset of this subgroup. We can prove it’s normal, and $S_n/A_n=C_2$.

When we were young, there was a sliding puzzle game (mostly with pictures, not numbers, but essentially the same). All operations involve moving these blocks to the correct positions, but if we want to swap just two blocks through operations (like swapping 14 and 15), it’s impossible. This is because each operation changes the position of the empty space, and each operation is essentially swapping the empty space with an adjacent block. Only an even number of moves can return the empty space to its original position, meaning we can only achieve even permutations, while simply swapping two blocks is an odd permutation, which is impossible.

Simple Groups

Now we can define a concept similar to prime numbers - simple groups - if all normal subgroups of a group are trivial ({e} and itself), this group is called a simple group. For example, all cyclic groups of prime order are simple groups. The question of which finite groups are simple is very interesting, see the article “Finite Simple Groups: A Century-Long Journey“.

It’s precisely because alternating group $A_5$ is simple that directly leads to quintic equations having no radical solutions. (To be continued)