#Warning: This article contains super advanced content, covering essentially all the basic algebraic theory of four-dimensional Euclidean space. This article emphasizes algebra over geometry, so it may be difficult to understand
This article will introduce a new algebraic system that can “unify” high-dimensional geometry: Geometric Algebra. This algebraic framework encompasses scalars, vectors, multidimensional vectors, as well as various inner products, outer products, and mixed products. It even includes spinors (the culprit that makes electrons need to rotate twice to look the same), spatial rotations, complex numbers and quaternions, various derivative operators in vector fields, and geometric algebra can even give a new definition of determinants…
Introduction
When we discussed magnetic fields in four-dimensional space, we mentioned three multiplication operations between two 2-vectors:
| Operation | $e_{ij}*e_{ij}$ | $e_{ij}*e_{jk}$ | $e_{ij}*e_{kl}$ |
|---|---|---|---|
| Inner product$\cdot$ | 1 | 0 | 0 |
| Mixed product$\times$ | 0 | $e_{ik}$ | 0 |
| Outer product$\wedge$ | 0 | 0 | $e_{ijkl}$ |
At that time, we felt that identical letters could be merged and canceled, while different letters were simply written together to form a multidimensional vector, so that each type of n-vector corresponds exactly to one multiplication operation. Let’s define a new multiplication operation to satisfy all the above conditions simultaneously. To distinguish it from inner and outer products, the new multiplication uses no symbol:
- For vector $\boldsymbol v$, we define $\boldsymbol v^2=\boldsymbol v \boldsymbol v=||\boldsymbol v||$. This is the definition of inner product.
- Then we “forcibly” incorporate the definition of outer product: for mutually perpendicular vectors $\boldsymbol u$ and $\boldsymbol v$, we define $\boldsymbol u \boldsymbol v = -\boldsymbol v \boldsymbol u$.
- We further stipulate that this multiplication satisfies associativity and left-right distributivity for any k-vectors $\boldsymbol A$, $\boldsymbol B$: $(\boldsymbol A \boldsymbol B) \boldsymbol C = \boldsymbol A (\boldsymbol B \boldsymbol C) $, $(\boldsymbol A+ \boldsymbol B) \boldsymbol C = \boldsymbol A \boldsymbol C +\boldsymbol B \boldsymbol C $, $\boldsymbol A( \boldsymbol B+ \boldsymbol C) = \boldsymbol A \boldsymbol B +\boldsymbol A \boldsymbol C $.
This new multiplication is the geometric product. For consistency, we define scalars as 0-vectors.
Let’s see what happens when two arbitrary vectors $\boldsymbol u$, $\boldsymbol v$ with angle $\theta$ form the geometric product $\boldsymbol u\boldsymbol v$. The definition only gives properties of the geometric product for vectors in parallel and perpendicular directions, so we first need to orthogonally decompose $\boldsymbol u$ onto $\boldsymbol v$:
$$\boldsymbol u = \boldsymbol e_{\parallel v}||\boldsymbol u||\cos \theta + \boldsymbol e_{\perp v}||\boldsymbol u||\sin \theta$$
$$\boldsymbol u \boldsymbol v = \boldsymbol e_{\parallel v} \boldsymbol v ||\boldsymbol u||\cos \theta + \boldsymbol e_{\perp v} \boldsymbol v ||\boldsymbol u ||\sin \theta=||\boldsymbol u||||\boldsymbol v||\cos \theta + e_{\perp v} e_v ||\boldsymbol u||||\boldsymbol v||\sin \theta = \boldsymbol u \cdot \boldsymbol v + \boldsymbol u \wedge \boldsymbol v$$
What? A scalar and a 2-vector added together? Does this make sense? This was my first reaction when I saw geometric algebra on Wikipedia, and then I clicked the close button in the upper right corner of the window. Later I gradually came to understand the power of geometric algebra. So let’s not talk about meaning first, let’s continue to see what happens when two 2-vectors form a geometric product.
Due to the complex spatial position of 2-vectors, we’ll compute directly using coordinates. Let
$$\begin{align} A&=a_1e_{xy}+b_1e_{xz}+c_1e_{xw}+d_1e_{yz}+e_1e_{yw}+f_1e_{zw} \\ B&=a_2e_{xy}+b_2e_{xz}+c_2e_{xw}+d_2e_{yz}+e_2e_{yw}+f_2e_{zw}\end{align}$$
$$AB=(a_1e_{xy}+b_1e_{xz}+c_1e_{xw}+d_1e_{yz}+e_1e_{yw}+f_1e_{zw})(a_2e_{xy}+b_2e_{xz}+c_2e_{xw}+d_2e_{yz}+e_2e_{yw}+f_2e_{zw})$$
The expansion calculation is somewhat large, but not difficult. The expanded terms may be in these cases:
- Completely identical, like $e_{xy}e_{xy}$: $e_{xy}e_{xy}=e_xe_ye_xe_y=-e_x(e_xe_y)e_y=-(e_xe_x)(e_ye_y)=-1$
- Partially identical, like $e_{xy}e_{xz}$: $e_{xy}e_{xz}=e_xe_ye_xe_z=-e_x(e_xe_y)e_z=-(e_xe_x)e_ye_z=-e_{yz}$
- Completely different, like $e_{xy}e_{zw}$: $e_{xy}e_{zw}=e_xe_ye_ze_w=e_{xyzw}$
Observing that after combining like terms, we get three parts added together: scalar part + 2-vector part + 4-vector part. It’s not hard to see that except for the scalar part differing by a sign, each part’s result is exactly the multiplication given in the opening table, so we have $\boldsymbol {A B}=-\boldsymbol A\cdot \boldsymbol B + \boldsymbol A\times \boldsymbol B + \boldsymbol A\wedge \boldsymbol B$.
Geometric Algebra is a Graded Algebra
We call this mixed vector containing different dimensions a Multivector. For a multivector $A$, we define a projection operator: $\left\langle A\right\rangle_k$ represents taking the k-vector part of multivector $A$. This way we can define the outer product using geometric algebra: (Here $\left\langle A\right\rangle_m$ and $\left\langle B\right\rangle_n$ represent two pure m-vectors and n-vectors)
$$\left\langle A\right\rangle_m\wedge \left\langle B\right\rangle_n=\left\langle\left\langle A\right\rangle_m\left\langle B\right\rangle_n\right\rangle_{m+n}$$
The inner product is more troublesome. First, inner product only exists between vectors of the same dimension, to ensure the result is a real number. And the inner product has positive definiteness, meaning a non-zero quantity inner producted with itself needs to yield a result greater than 0. We see that $e_{xy} e_{xy}=-1$, it feels like $e_{xy}$ is $\sqrt{-1}$. When computing inner products with complex numbers, we need to take the conjugate of the second term to ensure the result is real. So we also define a conjugate transpose operation: $(e_1e_2..e_n)^\dagger=e_n..e_2e_1$, and define the inner product of A and B as $\left\langle AB^\dagger\right\rangle_0$, which can exactly eliminate all letters directly without exchanging any vectors, so no negative sign is produced.
Representation of Rotation
Orthogonal Matrices and Generators
We know that rotation in n-dimensional space can be represented by n-dimensional orthogonal matrix $R$, satisfying $RR^T=R^TR=I$. But rotation in real life is a dynamic process. Strictly speaking, orthogonal matrix $R$ only represents the final rotation result. How can we capture the dynamics of rotation? Suppose we rotate at a certain angular velocity, the rotation matrix is actually a function of time $t$: $R(t)$, which represents that after time $t$, vector $x$ rotates from initial position $x_0$ to $R(t)x_0$. Now let’s explore the motion of each point in space at a certain instant during rotation, directly taking the derivative with respect to $t$ to get the velocity at each point:
$$v=\dot x=\dot R(t)x_0$$Since we assume uniform rotation, the velocity field $\dot R(t)$ explicitly contains time only because each point rotates to different positions, and the velocity direction will of course keep changing. If we write $\dot R(t)=BR(t)$, that is, examining the relationship between the rotation velocity field of all points and their relative positions, $B$ is a constant, which is actually a matrix representation of angular velocity.
If we first specify the velocity distribution $B$, can we deduce the rotation matrix after rotating for a specified time $t$ at this velocity? This is equivalent to solving a differential equation:
$$\dot x(t)=Bx(t)$$
How do we solve a matrix differential equation? Observing, it’s actually similar to a general linear differential equation:
$$y’=by$$
Its solution is exponential, so we also define an exponential operation for matrices:
$$\exp(M)=I+M+{M^2\over2!}+{M^3\over3!}+..$$
We can verify that $x(t)=\exp(Bt)x_0$ is the solution to the equation, meaning the rotation matrix is $\exp(Bt)$, but note that $B$ must satisfy a condition to ensure $\exp(Bt)$ is orthogonal:
$I=\exp(Bt)\exp(Bt)^T=\exp(Bt)\exp(B^Tt)=\exp((B+B^T)t)$
Note that through the matrix exponential definition, not all matrices satisfy $\exp(A+B)=\exp(A)\exp(B)$, unless $AB=BA$.
For $\exp((B+B^T)t)$ to always be $I$, we can only have $B=-B^T$, meaning all $B$ that can generate rotation matrices must be antisymmetric. We call the $B$ corresponding to a rotation the matrix’s generator. Besides understanding the generator as angular velocity, it can also be understood as infinitesimal rotation: imagine all points in space moving a little bit in the direction of the velocity field, i.e., $x + \Delta x = (I+\Delta\theta B)x$, and all rotations can be considered as going through infinite infinitesimal rotations: $R=(I+\Delta\theta_1 B_1)(I+\Delta\theta_2 B_2)(I+\Delta\theta_3 B_3)..$
Spinors and Generators
Comparing, we can see that rotation generators correspond one-to-one with 2-vectors. This inspires us whether we can describe spatial rotation using geometric algebra methods instead of matrices.
Suppose there is a unit vector $a$. Using coordinate decomposition, it’s not hard to prove that $ava$ is also a vector, which is the reflection of $v$ with respect to $a$. Rotation can be decomposed into an even number of reflections, so we get the geometric algebra version of rotation representation: Let $R=r_1r_2..r_{2k}$, and $RR^\dagger=1$, then $RvR^\dagger = r_1r_2..r_2k v r_{2k}..r_2r_1$ rotates vector $v$. $R$ has a special name, called a spinor or rotor.
We can also prove that $(RvR^\dagger)\cdot(RuR^\dagger)=v\cdot u$, showing that it preserves inner products and is indeed an orthogonal transformation. But such $R$ generally mixes several even-dimensional vectors, so here we find the meaning of geometric algebra adding vectors of different dimensions together, though I admit this addition is very unintuitive. For example: rotation by 60° in the $xy$ plane can be generated by spatial reflection vectors $r_1=e_x$ and $r_2=\sqrt{3}/2e_x+1/2e_y$, then $R=r_1r_2=\sqrt{3}/2+1/2e_{xy}$.
Now the same question arises: given a unit 2-vector $B$ (understood as rotating at unit angular velocity) and angle $\theta$ (understood as rotation time), how do we get $R$? First, we should describe angular velocity in the language of geometric algebra. Note that $Bv$ is not necessarily a vector, so we can’t copy the matrix method directly. But we can verify that when $v$ is parallel to $B$, $Bv$ is the velocity at point v, but when $v$ is perpendicular to $B$, $Bv$ is a 3-vector. We can use the projection operator to keep only the 1-vector part, but the projection operator is inconvenient for subsequent operations. We also observe that for the 3-vector part we have $Bv=vB$, but for the vector part it’s $Bv=-vB$, so the 1-vector part can be extracted using ${1\over2}(Bv-vB)$. So we get the differential equation with respect to time $\theta$:
$${\text d\over\text d \theta}v(\theta)={1\over2}(Bv(\theta)-v(\theta)B)$$
Substituting the previous rotation expression $v(\theta)=R(\theta)v(0)R(\theta)^\dagger$, using the product rule for derivatives:
$$\dot Rv(0)R^\dagger+Rv(0)\dot R^\dagger={1\over2}(BRv(0)R^\dagger-Rv(0)R^\dagger B)$$
How do we solve for $R(\theta)$? Observing, we find that changing the second term $-B$ on the right to $B^\dagger$ gives:
$$\dot Rv(0)R^\dagger+(\dot Rv(0)R^\dagger)^\dagger={1\over2}(BRv(0)R^\dagger+(BRv(0)R^\dagger)^\dagger )$$
We see that both sides are in the form of transpose addition. We only need to solve for $\dot Rv(0)R^\dagger=BRv(0)R^\dagger/2$ to satisfy the original equation, simplifying to get
$$\dot R=BR/2$$
Obviously the solution to this equation is $\exp(B\theta/2)$, but note that $BR$ is multiplied together using geometric product, so $\exp(B\theta)$ defined through Taylor expansion here uses geometric product for all multiplications. Note the difference between the exponential map of geometric algebra and matrix exponential.
Let’s specifically calculate the expression for R:
$$R=\exp(B\theta/2)=I+B\theta/2+{B^2(\theta/2)^2\over2!}+{B^3(\theta/2)^3\over3!}+..$$
Note that for unit 2-vectors we have $B^2=-1$, so we can simplify using a method similar to deriving Euler’s formula:
$$\begin{align} R=&I+B\theta/2-{(\theta/2)^2\over2!}-{B(\theta/2)^3\over3!}+..\\=&I+B\theta/2-{(\theta/2)^2\over2!}+{B(\theta/2)^3\over3!}+..\\=&\cos(\theta/2)+B\sin(\theta/2)\end{align}$$
We finally get the expression for rotating vector $v$ by angle $\theta$ in plane $B$:
$$RvR^\dagger = (\cos(\theta/2)+B\sin(\theta/2))v(\cos(\theta/2)-B\sin(\theta/2))$$
Double Cover
What is the relationship between the rotation representation based on geometric algebra and the spinor related to electron spin? A vector rotated by $\theta$ corresponds to spinor $R$ rotated only by $\theta/2$. Since the rotation expression is $RvR^\dagger$, $R$ and $-R$ represent the same rotation, corresponding exactly to the case where after the vector rotates one full circle, the spinor $R$ changes sign. So each rotation corresponds to two spinor representations. In technical terms, the spinor group is a double cover of the rotation group.
We know that starting from four-dimensional space, rotations include not only simple rotations but also double rotations. Here we have already proven that any 2-vector in four-dimensional space can be decomposed into absolutely perpendicular simple 2-vectors. Through exponential mapping, we prove that any double rotation is a superposition of mutually absolutely perpendicular simple rotations. In that proof, we used a “dual coordinate system” specific to 2-vectors in four-dimensional space. The so-called dual coordinate system refers to decomposing a 2-vector into “self-dual” (satisfying $A=A^*$) and “anti-self-dual” (satisfying $A=-A^*$) parts. There’s a magical property that the geometric product of self-dual 2-vectors and anti-self-dual 2-vectors is 0, meaning all three multiplication operations yield 0. So the generated rotations can also be divided into two parts that can be reordered without interference: left isoclinic double rotation and right isoclinic double rotation. If the angles of left and right isoclinic rotations are equal, they combine into a simple rotation. For example, a 90° rotation in the xy plane can be seen as a superposition of 45° double rotation generated by $e_{xy}+e_{zw}$ and 45° double rotation generated by $e_{xy}-e_{zw}$.
Quaternions
We know that complex numbers are introduced with $i$—which satisfies $i^2=-1$. From this starting point, we can derive many geometric and algebraic properties. Of course, people have also tried to construct similar numbers extended to higher dimensional spaces. Below we’ll look at its four-dimensional extension—quaternions. We will give the geometric meaning of quaternions in four-dimensional space and reveal their true nature. According to our habit, we should first extend complex numbers to ternions, then to quaternions. However, after efforts by some mathematicians, they found that ternions don’t exist! Let’s first look at what quaternions look like:
$$i^2=-1, j^2=-1, k^2=-1, ij=-ji=k, jk=-kj=i, ki=-ik=j$$
We see that quaternion multiplication doesn’t satisfy commutativity! Initially, I found it hard to accept what meaning a system that doesn’t even satisfy commutativity could have, but we will see that quaternions can represent rotations in four-dimensional space. Just like in three-dimensional space, different orders of rotation give different results. For example, rotating 90° around the x-axis then 90° around the y-axis is not equal to rotating 90° around the y-axis then 90° around the x-axis.
Quaternions satisfy associativity like rotations, e.g., $(ij)k=kk=-1=ii=i(jk)$. In fact, all quaternions form a group, just like rotations form a rotation group (a group satisfies requirements like associativity, invertibility, and having an identity element for multiplication).
If you’re interested in why quaternions are defined this way, you can expand this section:
Various Quaternions
Quaternions in 3D Computer Graphics
Quaternions can represent four-dimensional rotation, so they can certainly represent three-dimensional rotation. Let’s first peek at quaternions from three-dimensional space. In fact, they are widely used in computer graphics. If you search for quaternions online, the most common content should be how to use quaternions to represent rotation around a given axis $l$ by a given angle $\theta$:
First, we stipulate that three-dimensional coordinates $(x,y,z)$ correspond to quaternions as $xi+yj+zk$. Note this quaternion has no real part, only three imaginary parts. Then map the unit vector parallel to axis $l$ to quaternion $L$ using the above method, then calculate quaternion $Q=\cos\theta/2 + L \sin\theta/2$. This quaternion represents rotation around the given axis $l$ by the given angle $\theta$. The new vector $x’$ obtained by rotating vector $x$ is calculated by the following formula, where $X$ and $X’$ are quaternions corresponding to the respective vectors:
$X’=QXQ^*$, where $Q=a+bi+cj+dk$, and we denote $Q^*=a-bi-cj-dk$, called the conjugate of $Q$.
The formula is given, and there’s no problem dealing with three-dimensional rotation calculations, just always pay attention that quaternions don’t have commutativity during calculations. But why does this give the correct rotation? The explanation based on geometric algebra is the most numerous and natural, for example see this article (the author is the person who developed 4DToys!)
Quaternions and Geometric Algebra
Quaternions are an extension of complex numbers. They’re somewhat like geometric algebra, not satisfying commutativity, and the property $ij=-ji$ is also similar. In fact, we can construct a subalgebra of geometric algebra in three-dimensional space that is isomorphic to quaternions: define $i=e_{xy},j=e_{yz},k=e_{zx}$. We can verify that the geometric products between $i,j,k$ satisfy the quaternion multiplication rules. So a general quaternion $q=a+bi+cj+dk$ can be written as $Q=a+be_{xy}+ce_{yz}+de_{zx}$, and its conjugate is exactly the transpose of the corresponding geometric algebra multivector $q^*\rightarrow Q^\dagger=a-be_{xy}-ce_{yz}-de_{zx}$. That is, unit quaternions $qq^*=1$ correspond exactly to spinors representing three-dimensional rotation $RR^\dagger=1$! Thus we naturally obtain the quaternion representation of three-dimensional rotation:
$$v’=qvq^*$$
Quaternions and Four-Dimensional Rotation
How about extending quaternions to four dimensions? It feels like quaternions should originally be products of four-dimensional space, but since the status of $1$ and $i,j,k$ are different, quaternions don’t have a very natural explanation in four-dimensional space! But if we write the vector $(x,y,z,w)$ as $x+iy+jz+kw$, we find that left multiplication by $i,j,k$ rotates the vector 90° left isoclinically, while right multiplication by $i,j,k$ is 90° right isoclinic rotation. It can be proven that for any unit quaternions $p,q$, $pvq$ represents a rotation in four-dimensional space, with $pv$ being the left isoclinic rotation part and $vq$ being the right isoclinic rotation part. The restriction $p=q^*$ in three-dimensional space is to confine the rotation within the three-dimensional space $yzw$.
Can quaternions be further extended to higher dimensions? Unfortunately, although there are octonions, they don’t satisfy associativity and are no longer suitable for representing spatial rotation. So for rotations in higher-dimensional spaces, the spinor representation must honestly use $R$.
Volume Elements, Orientation and Hodge Duality
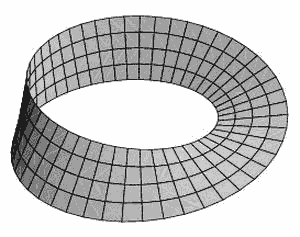
Imagine a group of two-dimensional beings living on a Möbius strip. The Möbius strip has no distinction between inside and outside, which we call a non-orientable surface. So if we choose a normal vector direction at a point on the strip, after going around the strip once, the normal vector reverses sign. But concepts like normal and inside/outside only exist in three-dimensional space. Can these two-dimensional beings, unable to leave the two-dimensional space of the strip (they cannot perceive the third dimension), know they are on a Möbius strip?
The answer is yes. One obvious characteristic is that after traveling around once, they find themselves mirror-reversed, like the directed circle in the figure. How do we describe this mathematically? We can use 2-vectors that also represent circles. Note that 2-vectors on a two-dimensional Möbius strip can only be parallel to the tangent space at each point, so there’s only one degree of freedom, feeling like scalars. But unlike scalars, you cannot define a continuous non-zero 2-vector field on the entire Möbius strip, though you can on a cylindrical surface. We see that 2-vectors are consistent with the description using normal vector reversal, but this description method doesn’t need to involve three-dimensional space, i.e., directions that don’t exist on the Möbius strip. Similarly, all n-vectors on n-dimensional surfaces have only one degree of freedom, called volume elements. If a continuous non-zero volume element field can exist on an n-dimensional surface, we say this surface is orientable; otherwise, it’s non-orientable. Different orientations differ in sign; we don’t care about the relative size of volume elements.
Left-handed and Right-handed Coordinate Systems
It’s well known that our world is orientable (at least within the locally observable universe). But there are two choices for orientation direction. Generally, we say a right-handed coordinate system is artificially specifying coordinate axes in xyz order. If the new coordinate axes are abc, we can determine whether it’s a right-handed coordinate system by calculating whether the volume element $x\wedge y\wedge z$ is consistent with the direction of $a\wedge b\wedge c$. Here we see that the size of the volume element in three-dimensional space is exactly the volume of the parallelepiped spanned by the three coordinate axes, hence called volume element.
Volume Elements and Determinants
We know that linear mappings (or matrices) have determinants. Below we use a new method to define the determinant of linear mapping $f$:
$$f(I)=\det(f)I$$
where $I$ is any volume element in the linear space, and the linear mapping acts on n-vector $e_1\wedge e_2..\wedge e_n$ as $f(e_1)\wedge f(e_2)..\wedge f(e_n)$. This definition reveals the essence of determinants: it’s the scaling factor for area/volume (depending on dimension) after linear mapping, and if the linear mapping changes the spatial orientation, the determinant value is negative.
Volume Elements and Hodge Duality
We can use unit volume element $I$ and geometric product to represent Hodge duality.
Define $A^*=A^\dagger I$, i.e., let A do “partial” inner product with unit volume element. Since the volume element contains all letters of the entire space, the original letters in A will be eliminated one by one with these letters to become scalars, leaving only letters not in A, thus obtaining the normal space of A.
Some Applications of Geometric Algebra Beyond Rotation
Proving Equations in Vector Field Theory
Let’s use geometric algebra to prove this equation encountered in wave equations ($E$ is a vector): $\nabla \times\nabla \times\boldsymbol{E}=-\boldsymbol{\Delta \boldsymbol{E}}+\text{grad}(\text{div}(\boldsymbol{E}))$
$$\begin{align}\nabla \times\nabla \times\boldsymbol{E}=&(\boldsymbol{d}\wedge(\boldsymbol{d}\wedge\boldsymbol{E})^*)^*\\=&-\left\langle\boldsymbol{d}(\boldsymbol{d}\wedge\boldsymbol{E})\right\rangle_1\\=&-\left\langle\boldsymbol{d}(\boldsymbol{dE}-\boldsymbol{Ed})/2\right\rangle_1\\=&-(\boldsymbol{d}(\boldsymbol{dE}-\boldsymbol{Ed})-(\boldsymbol{dE}-\boldsymbol{Ed})\boldsymbol{d})/4\\=&-(\boldsymbol{d}^2\boldsymbol{E}+\boldsymbol{E}\boldsymbol{d}^2)/4+\boldsymbol{dEd}/2\\=&-\boldsymbol{d}^2\boldsymbol{E}/2+\boldsymbol{dEd}/2\end{align}$$
$$\begin{align}-\boldsymbol{\Delta \boldsymbol{E}}+\text{grad}(\text{div}(\boldsymbol{E}))=&-(\boldsymbol{d}\cdot \boldsymbol{d})E+\boldsymbol{d}(\boldsymbol{d}\cdot \boldsymbol{E})\\=&-\boldsymbol{d}^2E+\boldsymbol{d}(\boldsymbol{dE}+\boldsymbol{Ed})/2\\=&-\boldsymbol{d}^2\boldsymbol{E}/2+\boldsymbol{dEd}/2\end{align}$$
Without geometric algebra, one would probably have to expand all coordinates honestly, but the geometric algebra method reduces most of the computational load.
Geometric Meaning of Various Products
We can now define multiplication operations for m-vector $A$ and n-vector $B$ in high-dimensional space: each k-vector component in multivector $AB$ corresponds to a multiplication operation of $A$ and $B$. We give the geometric meaning of these multiplications through the formula relating angles between two n-dimensional subspaces in N-dimensional space and the multiplication relationships of multidimensional vectors (not multi-level) representing the two subspaces: Generally, a hypersphere on an n-dimensional subspace projects onto another subspace as an n-axis hyperellipsoid. Through the axes of the hyperellipsoid, we can construct an n-dimensional orthogonal basis on the subspace. Projecting the orthogonal basis back to another subspace, linear algebra can prove it’s also orthogonal, and there are n pairs of orthogonal bases on the two subspaces corresponding through projection, with angles $\theta_1,\theta_2,..,\theta_n$. If not mutual projections, the two basis vectors are perpendicular. We use these n angles to measure the positional relationship between two n-dimensional subspaces.
We let the orthogonal basis on the first n-dimensional subspace be $u_1, u_2,..,u_n$, and the orthogonal basis on the second n-dimensional subspace be $v_1, v_2,..,v_n$. Then the two n-vectors representing the two subspaces are $A=u_1 u_2..u_n$ and $B=v_1 v_2..v_n$ respectively. Note that because of orthogonality, the outer product is the geometric product. Let’s derive all multiplication operations between A and B at once:
$$\begin{align}AB=&u_1 u_2..u_nv_1 v_2..v_n\\=&(u_1v_1) (u_2v_2)..(u_nv_n)(-1)^{n(n-1)/2}\\=&(\cos\theta_1+e_{u_1\wedge v_1}\sin\theta_1) (\cos\theta_2+e_{u_2\wedge v_2}\sin\theta_2)..(\cos\theta_n+e_{u_n\wedge v_n}\sin\theta_n)(-1)^{n(n-1)/2}\end{align}$$
Note the first step matches up the projected vectors, using the negative commutation law and associativity of perpendicular vectors. A total of $n(n-1)/2$ exchanges were made, so a sign needs to be added. The second step splits the geometric product of two unit vectors into inner and outer product representation, and the third step expands the parentheses. Note each parenthesis has only one scalar term and one 2-vector term, and these bivectors are absolutely perpendicular, so they can be directly combined when expanding. Thus the scalar term is $\cos\theta_1\cos\theta_2..\cos\theta_n(-1)^{n(n-1)/2}$; the 2n-vector term is $e_{u_1\wedge v_1}e_{u_2\wedge v_2}..e_{u_n\wedge v_n}\sin\theta_1\sin\theta_2..\sin\theta(-1)^{n(n-1)/2}$; for 2k-vector terms, it’s a combination of n-k cos and k sin, totaling $C_n^k$ terms that cannot be combined. These multiplications with both cos and sin are transitions from inner to outer products. Although finding angles this way is too troublesome compared to conventional pure linear algebra methods, it does give geometric interpretations of all multiplications between two n-vectors.