#This article explains episodes 7 and 8: Fiber bundles from the film “Dimensions: A Walk Through Mathematics“, with emphasis on the geometric properties of the Hopf fibration
Image from en.wikipedia by Niles Johnson
Featured Content
- Online WebGL 4D viewer
- Isoclinic planes
- Great ring structure of the 120-cell
- What is a fiber bundle
Table of Contents:
- Introduction
- Links
- Not Just Stereographic Projection
- Isoclinic Planes
- Great Ring Structure in the Regular 120-cell
- Orthogonality
- Four-dimensional Torus and Torus Eversion
- What is a Fiber Bundle?
Note: You may first refer to the film’s official website for detailed description of fiber bundles
Click to view 3D model of fiber bundle (requires WebGL-supported browser, such as Chrome)
Introduction
Let’s start today’s topic with a familiar example: the coordinate planes $xy$ and $zw$ intersect only at the origin. We have tried very hard to intuitively imagine the scenario where two infinite planes intersect at only one point, but we just can’t visualize it, leaving us with no option other than algebraic interpretation. Is there a more visual method? Here’s one way to visualize the positional relationship of these two planes simultaneously: place a unit hypersphere ($\mathbf S^3$) at the origin, which will certainly intersect all planes passing through the origin in unit circles. Now the problem becomes simple: we can directly see those unit circles by reducing dimensions to 3D space through stereographic projection.
Links
Since coordinate planes $xy$ and $zw$ only intersect at the origin, their intersection circles with the unit hypersphere do not intersect. What is the positional relationship when these two intersection circles are projected to 3D space? We can write a program to draw it: the stereographic projections of the two intersection circles are magically linked together like chain links! This chain-like figure is called a “Hopf link”.
We also want to see the intersection circles of more planes. The Hopf fiber bundle introduced in the film, obtained through complex numbers, achieves exactly this purpose—it allows us to better understand planes in 4D space (since all circles are obtained by planes passing through the origin), and also understand the wonderful properties of the hypersphere $\mathbf S^3$ itself. The introduction of complex numbers is the most ingenious part—the video explains it like this:
$z_2=k.z_1$ (Did you notice the detail in the film: French people use a dot for multiplication, and a comma for decimal points)
A very simple formula. Let’s explain in detail: first, choose an arbitrary plane $A$ in 4D space as coordinate axis $z_1$ (this axis is complex, so it’s 2-dimensional), then choose plane $B$ absolutely perpendicular to plane $A$ (since the coordinate system $z_1Oz_2$ is orthogonal) as coordinate axis $z_2$. For example, let’s choose the pair $xy$ and $zw$, specifically defining the calculation method from $(x,y,z,w)\to(z_1,z_2)$ (can be defined arbitrarily, this is just for convenience):
$$z_1=x+iy $$$$ z_2=z+iw$$
Substituting into the formula $z_2=k.z_1$ gives us the equation that the plane satisfies. Actually, complex multiplication in the formula $z_2=k.z_1$ doesn’t have a clear geometric meaning in 4D space. We’re just conveniently using complex numbers to randomly obtain a set of planes (different values of $k$ correspond to different planes), but the clever thing is that they are all pairwise linked!
$k$ can take any value in the extended complex plane (extended means $k$ can equal $\infty$, representing the plane $z_1=0$). We also know that stereographic projection can map a sphere ($\mathbf S^2$) to a plane plus a point at infinity, so we can consider $k$ as points taken on a 2-dimensional sphere, where each point on $\mathbf S^2$ (value of $k$) corresponds to a circle ($\mathbf S^1$) on the hypersphere ($\mathbf S^3$). Of course, taking $k$ points on this 2-dimensional sphere is purely a mathematical trick by Hopf to topologically construct the mapping $\mathbf S^1\to\mathbf S^3\to\mathbf S^2$, it has no direct concrete 4D geometric meaning. (Actually it does: the spherical distance between the $k$ values of two planes on this $\mathbf S^2$ is proportional to the angle between the two planes, but direct proof is tedious, an elegant proof might need inspiration from “complex projective line”?)
Not Just Stereographic Projection
The film contains many animations of stereographic projections of the Hopf fiber bundle. Actually, we can also view the Hopf fiber bundle from another angle—we can still see it using parallel projection. Various cylinders and cones in Dimensions Episode 3 on 4D space and the first article of this series used this method. Parallel projection doesn’t have as severe distortion as stereographic projection, but parallel projection causes many non-intersecting parts to appear intersecting, making the lines very messy.
Click to view 4D model online! Supports changing viewpoint in 4D space! (requires WebGL-supported browser, such as Chrome)
The lines are indeed messy, but we see that circles can sometimes project to line segments in 3D space, and looking from one end of the segment it shrinks to a point—thus we indirectly glimpse the shadow of planes intersecting at a point.
Return to Table of Contents
Isoclinic Planes
Obviously, the Hopf fiber bundle doesn’t represent all planes passing through the origin. For example, planes $xz$ and $yw$ can never be represented. (They have intersection points with unit circles on planes $xy$ and $zw$, so they don’t belong to this fiber bundle) We also sense that all Hopf fiber bundles have a common property. Later when we systematically study 4D space n-vector methods, we can calculate that the angles between them are isoclinic—that is, their $\theta_1=\theta_2$! This positional relationship of planes is called isoclinic. We can also prove that the set of all same-chirality isoclinic planes with respect to a plane forms exactly one complete Hopf fiber bundle. What is same-chirality? We’ll later introduce that all general position relationships between two planes can be divided into two symmetric classes like a person’s left and right hands. Remember the film “Dimensions” mentioned the Hopf circle and its mirror circle? They respectively form left and right-handed Hopf fiber bundles.
Great Ring Structure in the Regular 120-cell
Since Hopf fibers reflect properties of the hypersphere $\mathbf S^3$, and regular polytopes with many faces approximate hyperspheres (think of how regular polygons approximate circles in 2D), let’s see what secrets we can discover in the regular 120-cell. Its basic parameters are:
- 120 regular dodecahedral cells, 720 pentagonal faces, 1200 edges, 600 vertices;
- Dihedral angle between adjacent cells is 144°.
- See the previous article for layer structure
As mentioned before, the entire regular 120-cell can be divided into 12 great rings, with 10 regular dodecahedra on each ring connected end-to-end. To clearly describe the relative positions of these rings, let’s assign some codes to the layer structure:
| Layer | North/South Pole | Polar Circle | Mid-latitude | Tropic | Equator |
|---|---|---|---|---|---|
| Cell count | 2 | 24 | 40 | 24 | 30 |
| Code | $1$ | $12^1$ | 20 | $12^2$ | 30 |
We add N or S to represent north and south hemispheres, the equator doesn’t need this. The distribution of layer numbers for dodecahedra on the 12 rings of 10 elements has four types:
- $-N1-N12^1-N12^2-S12^2-S12^1-S-S12^1-S12^2-N12^2-N12^1- (1\times 10)$
- $-N20-N12^1-N12^1-N20-30-S20-S12^1-S12^1-S20-30- (5\times 10)$
- $-N12^2-N20-N20-N12^2-30-S12^2-S20-S20-S12^2-30- (5\times 10)$
- $-30-30-30-30-30-30-30-30-30-30- (1\times 10)$
The first group’s ring corresponds to the ten red dodecahedra in the image above, the fourth group’s ring corresponds to the orange dodecahedra ring lying flat in the middle. The 5 rings in the second group are closely interlinked with the first ring (red), the 5 rings in the third group are closely interlinked with the fourth group’s ring (orange).
If we draw these 12 great circles in the Hopf fiber bundle, the distribution of the 12 complex numbers $k$ corresponding to the planes containing the great circles on the sphere $\mathbf S^2$ is exactly the distribution of the 12 vertices of a regular icosahedron! This shows that these 12 rings actually have equal status. These beautiful properties of the regular 120-cell are exactly why I love it.
Orthogonality
Fiber bundles have many beautiful geometric properties. The six coordinate planes can be divided into three absolutely perpendicular pairs: $xy-zw$, $xz-wy$, $xw-yz$, so we have three ways to choose the planes corresponding to $z_1$ and $z_2$:
$$ z_1=x+iy; z_2=z+iw $$$$ z_1=x+iz; z_2=y+iw $$$$ z_1=x+iw; z_2=y+iz $$
Actually we can also swap real and imaginary parts:
$$ z_1=x+iy; z_2=w+iz $$$$ z_1=x+iz; z_2=w+iy $$$$ z_1=x+iw; z_2=z+iy $$
The first three groups actually describe the left-handed Hopf fiber bundle, the last three groups are right-handed fiber bundles: swapping the positions of two coordinate variables is equivalent to doing a spatial reflection transformation, so $z_1=y+ix; z_2=w+iz$ and $z_1=x+iy; z_2=z+iw$ have swapped two variables, reflected twice and returned to itself, they are both left-handed (actually Hopf fibers have central symmetry, they represent the same fiber bundle).
Let’s all choose left-handed Hopf fibers and draw these three fiber bundles simultaneously: they are orthogonal everywhere.
Click to view 3D model (requires WebGL-supported browser, such as Chrome)
They are orthogonal at every point in space: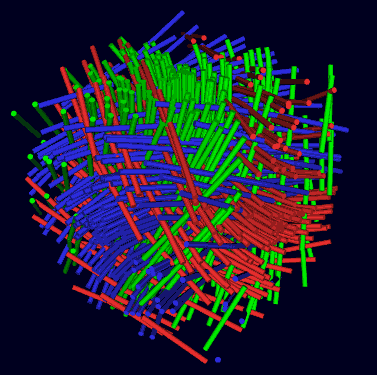
Four-dimensional Torus, Torus Eversion and Other Topological Problems
Why can these Hopf circles form a torus-like toroidal surface? Note: the torus you see here is just a 3D projection in 4D space, so we need to calculate its original expression: through simple calculation we can get that this torus’s equation in the 4D coordinate system is:$$\begin{cases}x^2+y^2=|z_1|^2 \\ z^2+w^2=|z_2|^2\end{cases}$$We can consider this as part of the surface of a new 4D geometric object:$$\begin{cases}x^2+y^2\le |z_1|^2 \\ z^2+w^2\le |z_2|^2\end{cases}$$This geometric object is something similar to a cylinder (note it’s certainly not a cylindrical column). Wikipedia calls it a “duocylinder”, meaning “double cylinder”. We will discuss it in detail in the next section along with a similar class of shapes called “duoprisms” (literally translated as “double prisms”), and thereby explain why meridians and parallels can actually be swapped when a torus is turned inside out.
Return to Table of Contents
Torus Eversion
While studying 4D space, we unexpectedly encountered 3D geometric knowledge like two circles linked like chains, and torus cross-sections showing two intersecting circles. Actually, stereographic projection also demonstrates another topological property of the toroidal surface: a torus with a hole can be turned inside out.
What is a Fiber Bundle?
Direct Product
When talking about fiber bundles, we first need to explain what a direct product is: Let $A$ and $B$ be any two sets. Take any element $x$ from set $A$ and any element $y$ from set $B$ to form an ordered pair $(x,y)$. Taking such ordered pairs as new elements, the set of all of them is called the direct product of sets $A$ and $B$, denoted as $A×B$, that is $A×B={(x,y)|x∈A$ and $y∈B}$.
Some examples:
- If $x$ is a line segment and $y$ is a line segment, $x×y$ is a rectangle.
- If $x$ is a circle and $y$ is a line segment, $x×y$ is a cylinder.
- $R$ is originally the set of real numbers, $R×R =〡(x,y)〡x∈R,y∈R〡$ is the set of all points on the $xy$ plane, $R×R$ is often written as $R^2$.
What if $x$ is a circle and $y$ is also a circle? Two 2D shapes will produce a 4D shape through direct product! What would it look like? We leave this as a thinking question, which will be discussed in detail in the next section
Direct Product and Fibers
What’s the relationship between direct product and fibers? We can understand direct product this way, for example, a cylinder can be seen as made up of many line segments or many circles:
You can see the appearance of “fibers”. But the fiber structure produced by direct product is simple and not very interesting, we call it a trivial fiber bundle.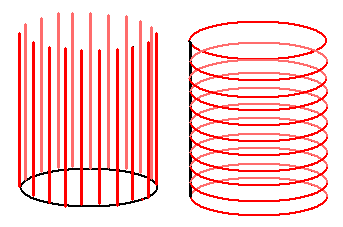
The simplest non-trivial bundle: Möbius strip
Look at the division of the Möbius strip—it looks like vertical generating lines on a cylinder—so locally it looks like the direct product of its edge and a vertical line, but overall it has an extra twist, so it’s fundamentally different from a cylinder and doesn’t satisfy the definition of direct product: {(x,y)|x∈A and y∈B}.
So we abstractly define fiber bundle: each fiber bundle is a continuous surjection $π: E → B$ such that $E$ locally looks like the direct product space $B × F$ for some $F$ (called the fiber).
A visual explanation: there’s a bunch of fuzzy fibers filling a portion of space $E$ (without gaps), the endpoints of these fibers are all on a surface $B$, any point in the fiber-filled space $E$ corresponds to a fiber, this fiber’s root corresponds to a point on surface $B$, i.e., the surjection $π: E → B$. In 4D space, besides the Hopf fiber bundle there are also Seifert fiber bundles (appearing in the Dimensions trailer) and others, which we will see later.
For the Hopf fiber bundle, E is the hypersphere $\mathbf S^3$, B is the sphere $\mathbf S^2$, F is the circle $\mathbf S^1$. Of course circles have no endpoints, this is just a visual explanation that each point on the sphere corresponds to a circle in the hypersphere. Topology is very enthusiastic about finding various mappings between n-dimensional spheres $\mathbf S^n$! For example, they discovered that similar fiber bundles exist in 7-dimensional space, but unfortunately we can no longer clearly visualize that dimension.