4D World (XI): The Periodic Table

This time we’ll look at the periodic law of elements in the microscopic theory of the 4D world. The atomic structure in four dimensions has always been a troublesome matter: the inverse cube law of force decay leads to the non-existence of stationary atomic wave functions, and the scientific community agrees that atoms cannot exist in a 4D world, nor can matter be formed, end of article. Besides directly accepting this cruel reality, we can actually assume there are 4D atoms, but their quantum mechanical mechanisms must be completely different from 3D theory. To maintain similarity with our world as much as possible, if we temporarily ignore the inverse cube law of forces and assume that the distribution of wave functions in various directions on the hypersphere still satisfies wave dynamics, then we can still preserve the electron subshell structure of atoms, the periodic law of elements, and molecular structures. The shortcoming is that calculations involving overall energy such as ionization energy, reactivity, and spectra that need to consider the radial direction would be completely unpredictable. Therefore, the “scientific validity” of this article (including the entire 4D world series) is greatly reduced, and is only for entertainment and providing ideas (for writing novels, etc.). Please don’t take it too seriously.

Review: 3D Periodic Law

How does the periodic law of 3D elements come about? Simply put, in the microscopic world, everything is a quantum wave. Electrons outside the atomic nucleus are standing waves vibrating around the nucleus. Solving these vibration modes through mathematical equations gives us what are called electron orbitals. Due to the characteristics of electron wave functions, two electrons cannot be in exactly the same vibration mode simultaneously, so each electron orbital can accommodate at most two electrons with opposite spins - this is the Pauli exclusion principle.

If readers have seen the spherical harmonics introduced in the previous article 4D Space (XIII): Hyperspherical Harmonics, we can start arranging elements: The electron wave function vibrates in 3D space. Besides spherical harmonics representing vibrations on the sphere, we also need to add radial vibrations. The total number of vibrations represents energy, i.e., the electron’s “shell”. If total vibration is 0, there’s only one spherically symmetric wave function, corresponding to the $1s$ orbital. This orbital can contain one or two electrons, corresponding to hydrogen and helium elements.

For lithium, the lowest energy orbital is filled, and the extra electron must squeeze into the next shell - orbitals with vibration of 1. If the vibration is in the radial direction, the wave function is still spherically symmetric, corresponding to the $2s$ orbital. If the vibration is on the spherical surface, there can be no more radial vibration, and there will be three vibration modes on the sphere, corresponding to three 2p orbitals: $p_x$, $p_y$, $p_z$. The difference between $s$ and $p$ orbitals lies only in the magnitude of angular momentum. In principle, electrons should fill based on energy priority, but in reality, interactions between electrons cause these orbitals with different angular quantum numbers to have different actual energies, following a diagram called “energy level crossing” that you’ve probably seen in high school chemistry.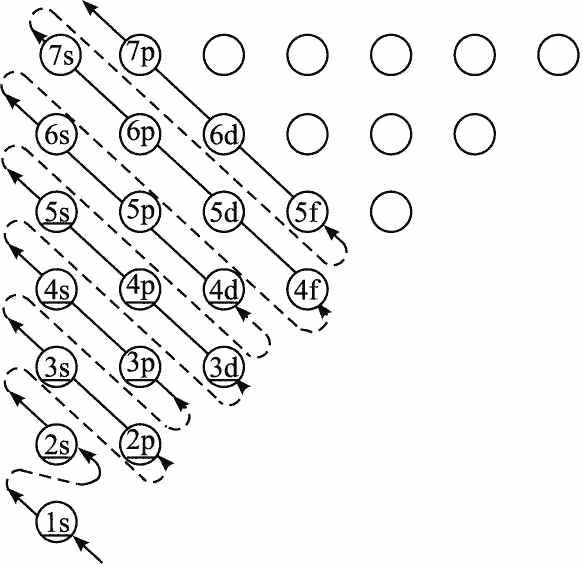

With the energy level crossing principle, continuing to fill electrons in order can explain why there are main groups, transition groups, and lanthanides, actinides… In short, given an angular quantum number $l$, there exist $2l+1$ degenerate orbitals (meaning these orbitals all have the same angular quantum number), i.e., each electron shell has at most one $s$ orbital, 3 $p$ orbitals, 5 $d$ orbitals, 7 $f$ orbitals… I believe everyone is already quite familiar with the 3D periodic table (high school level). Before continuing to four dimensions, let’s first look at the periodic law in the simpler 2D world to deepen our understanding of these principles.

Practice: 2D Periodic Law

The book “Planiverse” has already envisioned a 2D universe and its periodic table. It assumes electrons still have two spin states (clockwise and counterclockwise) and also follow the energy level crossing diagram. We discussed vibrations on a circle in the previous article - they are simply classified by the number of vibrations. Except for the constant function, each vibration number has two phase vibration modes similar to sine and cosine. The vibration number corresponds exactly to the angular quantum number, so except for its $s$ orbital which has only one, all other orbitals ($p$, $d$, $f$, $g$, etc.) have two. Each orbital can hold at most two electrons. Following energy level crossing, we get a zigzag periodic table shaped with every two rows and every four columns. The image below comes from a Bilibili user’s column.

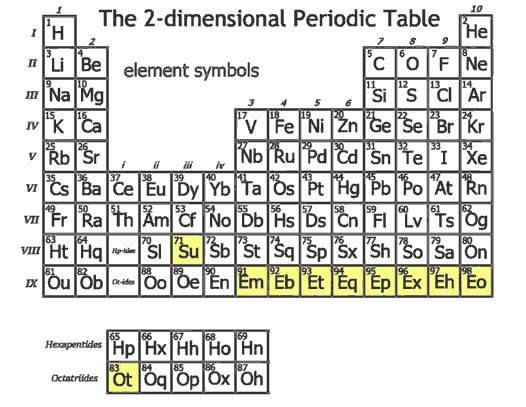
We can see that the main groups, transition groups, and lanthanide/actinide series in the 2D world all have only 4 columns, much shorter than in three dimensions. This led the author to not need to separate out the $f$ orbital-generated lanthanides (Ce - Yb) and actinides (Th - No) like in the 3D periodic table (the author only separated them starting from the $g$ orbital). From this, we can see that the elemental diversity in the 2D world seems much less than in three dimensions, unless superheavy elements are much more stable than in three dimensions, allowing more superheavy elements to be added to make up the numbers.

There’s no nitrogen element in the 2D world - carbon is directly followed by oxygen. Carbon has only 3 electrons in its outer shell, needing 3 more for the stable 6-electron structure, so methane is CH₃ rather than CH₄. Similarly, ethylene has a linear structure H-C=C-H, and there’s no longer triple-bonded acetylene. Apart from carbonic acid, no other organic acids exist, and for aldehydes, there’s only formaldehyde, no acetaldehyde. Oxygen atoms haven’t changed much - water is still H₂O. Fluorine and other halogens aren’t much affected by dimensionality and are similar to three dimensions.

Attempt: 4D Periodic Law

Finally, it’s time for four dimensions. The somewhat complex hyperspherical harmonics introduced in the previous article can finally start serving us. According to the wave patterns of angular quantum numbers on various latitude and longitude lines of the hypersphere, we can obtain the number of degenerate orbitals for different subshells: $s$ has only one orbital, $p$ has four: $p_x$, $p_y$, $p_z$, $p_w$, while $d$ and $f$ orbitals have 9 and 16 respectively. Generally, for angular quantum number $l$, it has $l^2$ degenerate orbitals. (Note that whether choosing Hopf coordinates or hyperspherical polar coordinates, although the orbital shapes differ somewhat, the number of orbitals is the same.) After mastering this pattern, we can completely draw the 4D periodic table according to the energy level crossing rules. Someone on the Higher Space forum proposed a 4D periodic table, posting a screenshot of a table and naming each element with element symbols: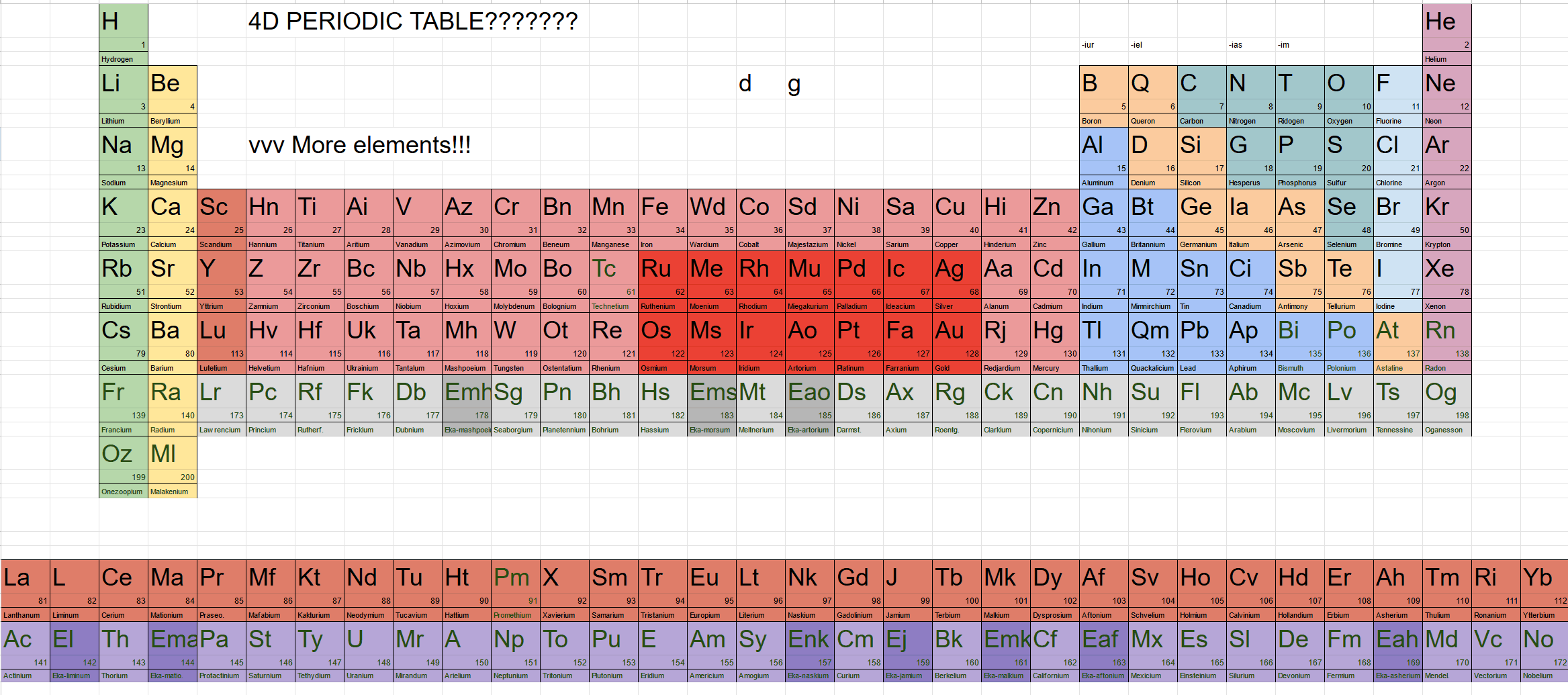

From this periodic table, the 4D periodic table looks very similar to the 3D one, except the main groups have two more columns, the transition groups are much longer, and the actinides and lanthanides are incredibly long - this is due to the greater number of $p$, $d$, and $f$ orbitals.

Common Compounds

For carbon atoms in the 4D world, the outermost shell has only 5 electrons, needing at most 10 to be full, so there’s one more type of hydrocarbon. I’ll still call single carbon-carbon bonded hydrocarbons alkanes - they have a pentachoron molecular configuration with sp⁴ hybridization. For the double bond structure, I chose the name “alkone”, which sounds between alkane and alkene, representing a new hydrocarbon class between alkanes and alkenes. Its molecular configuration is tetrahedral, with two lone electron pairs not participating in sp³ hybridization on both sides perpendicular to the tetrahedral cell. The triple bond structure resembles the planar triangular alkene class, using sp² hybridization with two mutually perpendicular lone electron pairs located on the plane absolutely perpendicular to the equilateral triangle. Finally, the linear form is the quadruple-bonded acetylene (ethyne) with sp hybridization.

We just saw pentavalent carbon. Besides monovalent, divalent, and trivalent fluorine, oxygen, and nitrogen, the biggest highlight of four dimensions is an additional tetravalent element between carbon and nitrogen. (this element is called N on the Higher Space forum, while nitrogen is called T). Its valence is four. Why say it’s more like nitrogen than carbon? Because it has 6 electrons in its outer shell, needing 4 more to reach a stable fully-filled structure, forming at most four bonds, with one already-filled lone electron pair remaining - in this respect it’s indeed more like nitrogen than carbon. According to valence shell electron pair repulsion theory, we can also predict that water molecules are bent, ammonia is trigonal pyramidal, entron-ammonia is tetrahedral pyramidal, methane is pentachoral…

Is This Really So?

I originally planned to continue exploring more complex organic structures like benzene, amino acids, and deoxyribonucleotides, but I suddenly realized - wouldn’t the double rotation effect in four dimensions mean electron spin states no longer have just two directions? If so, the periodic table just presented might be completely wrong, and the molecular structures would all be wrong too. To understand how 4D electrons actually spin, we’ll delve into the Dirac equation that describes electron motion in quantum field theory to explore the secrets of electron spin. This part requires a high level of physics and mathematics, so I’ll put it in optional reading - readers can completely skip it and go straight to the conclusion.

Optional Reading: Spin and Pauli Matrices

Electron Spin in the 3D World

In our world, electron spin has always been a mysterious phenomenon. Similar to how Earth has both orbital and rotational motion around the Sun, electrons have orbital angular momentum and spin angular momentum respectively. Orbital angular momentum is the electron’s wave function rotating around the atomic nucleus (p orbitals and above all have this), while spin angular momentum is like the electron’s rotation. Electrons are elementary particles, essentially just points - how can we sense their rotation? By detecting the magnetic moment produced by a charged object’s rotation.

In quantum mechanics, a particle’s position $r$ and momentum $p$ cannot be determined simultaneously, and orbital angular momentum $l=r\times p$ is composed of two “contradictory” quantities. This leads to only being able to measure the total magnitude of angular momentum and the angular momentum component in one direction when measuring angular momentum, but not all components of angular momentum simultaneously, because they would become uncertain like simultaneously determining position and momentum. Spin angular momentum is even stranger: besides following the same rules as orbital angular momentum (which quantities can and cannot be measured simultaneously), it has no other connection with the wave function in position space, similar to how Earth’s rotational orientation has no connection with its position in the universe. Therefore, besides the spatial wave function, we need to specifically introduce a quantum state in “internal space” to describe the spin state.

What exactly is the quantum state of electron spin? Everyone knows the electromagnetic field is a vector field with both orbital and spin angular momentum: when we rotate the entire space, both the electromagnetic field’s position in space (corresponding to orbital angular momentum) and the arrow direction (corresponding to spin angular momentum) rotate together, rather than rotating just one. Electron spin is similar to vector arrows - they both follow the rule of transforming under rotational transformations. Through studying the group representation theory of the rotation group, we can conclude: to satisfy rotation transformation rules, something must either be like a scalar (i.e., rotation-independent, always unchanging), or like a vector (like the electromagnetic field), or like some higher-order tensors (for example, gravitons are like symmetric second-order tensors, similar to an ellipse that returns to its original state after 180° rotation), or possibly like spinors - something we introduced in geometric algebra - which reverses sign after 360° rotation in space. People found that electron spin follows exactly the transformation rules of spinors.

At the time, people learned about electron spin magnetic moments through the phenomenon of two very close spectral lines appearing in atomic spectra, which also showed that electron spin angular momentum components can only take two discrete values. Scientist Pauli came up with three “Pauli matrices” - multiplying the Pauli matrices by $\hbar/2$ gives the spin angular momentum operators. $\sigma_z$ is already a diagonal matrix, indicating these two quantum states are exactly the eigenstates of z-axis spin angular momentum. Now it seems the z-axis is special, but actually not - we’ll introduce spinor rotation transformation rules that allow us to rotate any direction to the z-axis, thus eliminating this specialness.
$$\sigma_x=\begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix}$$$$\sigma_y=\begin{pmatrix}0 & -i \\ i & 0 \end{pmatrix}$$$$\sigma_z=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$
It’s easy to verify that these three matrices $\sigma_x$, $\sigma_y$, $\sigma_z$ all satisfy that their square equals the identity matrix, and multiplying any two matrices gives the third matrix, at most differing by a factor of $\pm i$. This means multiplication between Pauli matrices completely corresponds to the inner and outer products between 3D orthonormal vectors in geometric algebra, or in other words, multiplication between Pauli matrices completely corresponds to the geometric product of 3D orthonormal vectors. The three Pauli matrices are equivalent to three basis vectors in 3D space. If we rotate the entire space, then the three Pauli matrices viewed as three vectors should also be rotated. Mathematically speaking, Pauli matrices are actually the complex matrix representation of geometric algebra. Now knowing how Pauli matrices transform under rotation, we can write the spin angular momentum component operators in any direction - they’re all linear combinations of these three Pauli matrices, just like general 3D vectors are linear combinations of three orthonormal basis vectors.

Electron Spin in 4D Spacetime

It might be too difficult to jump straight to four dimensions, so let’s warm up first in familiar 3+1 dimensional spacetime: considering the relativistic electron spin wave function equation. The core of the wave equation in quantum mechanics is that the temporal frequency of the wave is proportional to the wave’s energy $\mathrm E$ (or Hamiltonian $\mathrm H$), i.e., $$i\hbar{\partial \psi \over \partial t}= \mathrm H \psi$$
The spatial frequency of the wave is proportional to the wave’s momentum $\mathrm p$, i.e., $$i\hbar{\nabla \psi }= \mathrm p \psi$$
If we substitute $\mathrm H={p^2\over 2 m}$, we get the classical Schrödinger equation similar to Newtonian mechanics. If we “square” both sides of the equation and substitute the relativistic energy relation $\mathrm H^2=\mathrm p^2c^2+m^2c^4$, we get the Klein-Gordon equation: $$\hbar^2({\partial^2 \over \partial x^2}+{\partial^2 \over \partial y^2}+{\partial^2 \over \partial z^2}-{\partial^2 \over c^2\partial t^2})\psi= m^2c^2\psi$$
However, it’s a second-order equation and cannot directly simulate evolution given an initial wave function like the Schrödinger equation. Additional conditions are needed, such as the “initial velocity” of wave function evolution, to uniquely solve it. Besides non-unique solutions, the Klein-Gordon equation also has the problem of allowing “negative energy” due to squaring… To solve these problems, Dirac took the square root of the Klein-Gordon equation, assuming $\mathrm H = c(\alpha_x\mathrm p_x+\alpha_y\mathrm p_y+\alpha_z\mathrm p_z+\beta mc^2)$ is first-order in spacetime components, obtaining the Dirac equation. Since $\mathrm H$ contains only spatial derivatives without treating spacetime equally, we multiply both sides by $\beta^{-1}$ and move the time derivative term over to get: $$i\hbar(\gamma_x\partial_x +\gamma_y\partial_y +\gamma_z\partial_z - \gamma_t\partial_t)\psi=mc\psi$$
These undetermined coefficients $\gamma_i$ are called Dirac matrices. For the square root operation to proceed smoothly, the undetermined coefficients of the first-order terms in the equation must be matrices rather than simple numbers, and multiplication between matrices must follow the geometric algebra multiplication rules mentioned earlier: since there are no cross terms after squaring, multiplication of different $\gamma_i$ and $\gamma_j$ must satisfy anticommutation to cancel out, and multiplying each with itself corresponds exactly to the coefficients of those second-order partial differential terms in the Klein-Gordon equation. If using geometric units (speed of light $c=1$), they exactly equal the squares of unit vectors under spacetime metric, i.e., perfectly corresponding to the 4D spacetime version of geometric algebra - $e_x^2=e_y^2=e_z^2=1$, but $e_t^2=-1$.

To satisfy the geometric algebra multiplication rules of 3D spacetime, these Dirac matrices must be at least 4-dimensional complex matrices. The four components of the wave function $\psi$ correspond to the two spin quantum states of electrons and antielectrons (positrons) respectively.

Electron Spin in the 4D World

Actually, with slight modification we can transform the Dirac matrices in 4D spacetime into “Pauli matrices” in 4D pure spatial geometry. In the geometric algebra of 4D spacetime, $e_t^2=-1$, meaning one of the Dirac matrices squared is the negative identity matrix. We now want to construct an algebra where all four matrices squared equal the identity matrix. After some attempts, it’s not hard to obtain the following solution:
$$\sigma_x=\begin{pmatrix}0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ 0&1&0&0\end{pmatrix}$$$$\sigma_y=\begin{pmatrix}0&0&i&0 \\ 0&0&0&-i \\ -i&0&0&0 \\ 0&i&0&0\end{pmatrix}$$$$\sigma_z=\begin{pmatrix}0&0&0&i \\ 0&0&i&0 \\ 0&-i&0&0 \\ -i&0&0&0\end{pmatrix}$$$$\sigma_w=\begin{pmatrix}0&0&0&1 \\ 0&0&-1&0 \\ 0&-1&0&0 \\ 1&0&0&0\end{pmatrix}$$

Since angular momentum is a 2-vector, we might assume that $\sigma_a\sigma_b$ multiplied by a coefficient gives the spin angular momentum operator component on the coordinate plane $ab$. Note that 3D Pauli matrices use Hodge duality (for example, $\sigma_x\sigma_y=i\sigma_z$), so only vectors appear. After calculating these matrices representing 2-vectors, we find that two sets of matrices are indeed diagonalized, indicating we’ve found some spin eigenstates of 4D electrons:
$$\sigma_x\sigma_y=i\begin{pmatrix}-1&0&0&0\\0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&-1 \end{pmatrix}$$$$\sigma_z\sigma_w=i\begin{pmatrix}1&0&0&0\\0&-1&0&0 \\ 0&0&1&0 \\ 0&0&0&-1 \end{pmatrix}$$
They correspond to spin angular momentum in the $xy$ and $zw$ directions. From the above results, they’re both two-valued. They’re both diagonal matrices, indicating these two operators commute, ensuring we can measure their values simultaneously: the angular momentum components in the $xy$ and $zw$ directions for these four quantum states can only be $\pm\hbar/2$, similar to electrons in familiar 3D space.

Similar to discussing the angular quantum numbers of orbital angular momentum, let $\sigma^{+}=(\sigma_x\sigma_y+\sigma_z\sigma_w)/2$ and $\sigma^{-}=(\sigma_x\sigma_y-\sigma_z\sigma_w)/2$. These two operators correspond to measuring the left isoclinic rotation component $(e_{xy}+e_{zw})/2$ and right isoclinic rotation component $(e_{xy}-e_{zw})/2$ of the electron spin angular momentum operator. We find these two matrices are block-diagonal, indicating that electron spin can be further divided into left isoclinic “up”, “down” and right isoclinic “up”, “down” - four states. In the previous article, we drew tables showing that angular momentum components under various total angular quantum numbers can only take certain specific values. Now it’s time to add electron spin:

In the above figure, the grid center corresponds to states with all angular momentum components being 0. The gray grid’s vertical and horizontal directions correspond to angular momentum components on the $xy$ and $zw$ planes, with one grid representing one quantum number (angular momentum corresponding to one $\hbar$). The blue grid’s diagonal vertical and horizontal directions correspond to $(e_{xy}+e_{zw})/2$ and $(e_{xy}-e_{zw})/2$, the left and right isoclinic (Hodge self-dual and anti-self-dual) angular momentum components respectively, with one grid representing half a quantum number, i.e., angular momentum corresponding to $\hbar/2$.

Combining the two angular momentum bases just discussed, we can see that electron spin and orbital angular momentum have exactly opposite properties: orbital angular momentum is all simple rotation, while electron spin is all double rotation. If electron spin were simple rotation, it couldn’t be an eigenstate, only a superposition state. Such simple rotation states are unobservable because as soon as electron spin is measured, it “collapses” to a definite double rotation state.

Optional within Optional: Electron Spin in N-Dimensional Worlds

We just derived electron spin in the spatial part of the 4D world. In spacetime, it needs to follow the Dirac equation in 4+1 dimensional spacetime: the multiplication of the 5 coefficient $\gamma$ matrices should correspond to representing the geometric algebra in 4+1 dimensional spacetime.
$$i\hbar(\gamma_x\partial_x +\gamma_y\partial_y +\gamma_z\partial_z +\gamma_w\partial_w- \gamma_t\partial_t)\psi=mc\psi$$
What order are the current $\gamma$ matrices? Mathematically, it can be derived that for $m+n$ dimensional spacetime, the complex matrix representation of its geometric algebra must be at least of order $2^{\lfloor{m+n\over 2}\rfloor}$, where $\lfloor . \rfloor$ is the floor function. That is, the $\gamma$ matrices for 4+1 dimensional spacetime are also 4D.

For the 2D world, we can also apply the dimension formula above. The order of Pauli matrices in 2D space is $2^{\lfloor{2\over 2}\rfloor}=2$, exactly corresponding to electron spin having only clockwise and counterclockwise directions. Their Dirac equation corresponds to geometric algebra in 2+1 dimensional space, with matrix representation order $2^{\lfloor{(2+1)\over 2}\rfloor}$ still being 2 due to rounding. If there’s a five-dimensional world, we can calculate that electron spin still has 4 states, but in 6 dimensions it becomes 8 states: we group coordinate planes in pairs, forming three mutually independent absolutely perpendicular angular momentum components, each with “up” and “down” spin states, giving a total of 8 through permutation. The pattern for higher dimensions increasing with dimension is that electron spin states double every even dimension, remaining unchanged for odd dimensions. For more details, see the Wikipedia article Higher-dimensional gamma matrices.

Correction: Final Version of the 4D Periodic Table

Now we can conclude about electron spin in 4D atoms - it indeed has left isoclinic “up”, “down” and right isoclinic “up”, “down” four states, with spin still being 1/2, and electrons remain fermions. (2025.05 correction: Actually, the number of electron spin states in 4D atoms cannot be directly deduced and must be determined according to “experiments” in the 4D world: 4denthusiast proposed a worldview with only left isoclinic “up”, “down” two states. Although having only left-handed without right-handed is strange, our real world also has weird things like parity violation. This blog defaults to both left and right-handed electrons existing in nearly equal numbers.) According to the Pauli exclusion principle, fermions in the same state cannot have all quantum numbers identical, so one atomic orbital can hold 4 electrons. Compared to two and three dimensions where one orbital holds two electrons, the periodic table length will double:

1. Each shell’s s orbital has 1, holding 4 electrons;
2. Each shell’s p orbitals have 4, holding 16 electrons;
3. Each shell’s d orbitals have 9, holding 36 electrons;
4. Each shell’s f orbitals have 16, holding 64 electrons.

This periodic table is very large. Together with netizen Ningning, I created a complete 7-row table with 396 elements (finding so many Chinese characters with metal radicals was quite a challenge). Since the d transition series is already very long (36 columns), not to mention the actinides and lanthanides (64 columns), I initially thought of two layout methods: the first was directly similar to the 3D periodic table layout, the second was to list the d transition series separately like actinides and lanthanides, then also break each row of actinides and lanthanides in the middle. But later I found the second one too ugly and didn’t use it. Although the first is very long, it still looks beautiful when laid out:

Here are several formats of the 4D periodic table available:

• For desktop, recommended to view online in a separate browser tab (note that mobile default fonts may not display all characters fully);
• Download PDF document;
• Download png image;
• Download editable Excel version. for readers using Simplified Chinese, recommend also installing the Chemical4D font file.

Incidentally, here’s the design philosophy for the periodic table:

• Referencing the periodic table from the Higher Space forum, I doubled its length and multiplied element column numbers by two to fill even-numbered positions (with exceptions for alkali metals, halogens, and a few other elements). Odd-numbered elements are additionally added due to four spin states, generally named based on neighboring elements’ names or properties, or commemorating famous people (like “Eulerium” commemorating mathematician Euler), with some random or meme names. This also occurs in the name given from the Higher Space forum. (e.g. “Miegakurium” and “Mashpoenium”)
• All elements from the 3D world appear in corresponding positions in this table, and the Higher Space forum’s periodic table also follows this rule.
• When selecting Chinese names, I used Chinese characters included in Unicode. Some characters only have traditional versions, which I simplified by editing the font.
• 4D beings would draw these 4D periodic tables on 3D paper, so the table should also be 3D. Readers can think about how to specifically design this.

Lowest Energy Principle and Hund’s Rule Exceptions

In the 3D world, electrons filling orbitals first fill one by one in the same direction, then pair up in opposite directions. This is because electron energy is lowest when spin directions are consistent - imagine electrons as small magnets that spontaneously maintain consistent direction. When there are too many electrons and filling in the same direction would violate the Pauli exclusion principle, they squeeze into the same orbital with opposite spins.

In the 4D world, we use arrows in four directions to represent four spin directions. 《4D World (VIII): Geography and Navigation》 already analyzed that left-handed and right-handed isoclinic double rotation magnetic dipoles have no interaction with each other. Therefore our arrows are also 90 degrees apart, with interaction energy between consistent and opposite orientations. Electrons will preferentially fill all empty orbitals with the same chirality and orientation, then fill with another chirality same orientation, then fill the remaining two spin directions.(25.04.10 correction: Left-handed and right-handed magnetic dipoles do interact, but same-chirality magnetic dipoles have no interaction, so arrow directions won’t be forced to fill consistently. Therefore, orbital filling order might be very chaotic, with specific behavior beyond my predictive ability. For now, I’ll still assume electrons preferentially occupy as many cells as possible.)

Hund’s rule exceptions tell us that electron shells are most stable when fully filled, and half-filled is also relatively stable. We can assume that in 4D space, electron shells with 1/4 filled and 3/4 filled states still have some stability, but these two states are still not as stable as half-filled and fully filled. This causes some transition metal elements’ electron configurations to no longer strictly follow the energy level crossing order. For example, copper’s electron configuration is 3d³⁶4s² (3d fully filled, 4s half-filled), rather than 3d³⁴4s⁴, similar to the 3D world situation.

Properties of Common Elements

Since the number of electrons has doubled, we can naturally assume that under normal circumstances, covalent compounds no longer share 2 electrons to form bonds, but need 4 electrons instead. Taking the first row elements protium, deuterium, and tritium as examples, they can form the following compounds to achieve the noble gas helium’s electron configuration.

Here I borrowed the names of hydrogen isotopes to name the three elements in the first period - they’re all called “hydrogen elements” as their elemental densities are all lighter than air (In Chinese, “hydrogen”(氢) means “light weight”(轻)). Protium’s elemental form is H₄, because each protium atom has only one electron and needs four together to gather four electrons for a stable structure. We see that chemical bonds can now be formed between multiple atoms jointly, with bonding methods much richer than in three dimensions. Starting from the second period, valence electrons include one s orbital plus 4 p orbitals - 5 orbitals with 20 electrons total. Nonmetals generally tend to gain electrons to form neon’s outer electron structure.

Since the periodic table length has doubled, the variety of compounds these elements can form through permutation and combination is much greater than in the 3D world. Content that might take a small section in the 3D world would probably need a whole chapter for the 4D world. The next article will explore what chemistry in the hypothetical 4D world would be like, following explorers’ footsteps to 4D Earth-like planets, analyzing surface atmospheric composition and crystal structures of various 4D minerals.

Thought Questions

This article ends with some questions for readers to think about. Reference answers will be revealed in the next article. (Disclaimer: Since these are all forced assumptions, the answers are only for reference and entertainment, not representing correctness. Just don’t treat me as a crank…)

1. What molecules can protium (H: 1s¹) and oxygen (O: 1s⁴2s⁴2p¹²) form? What about deuterium (D: 1s²) and oxygen?
2. What are the possible structures for molecules similar to “water” in the 4D world?
3. What are the possible structures for molecules similar to “benzene” in the 4D world?
4. What is the most likely structure for elemental tritium (T: 1s³)?
5. What are the structures of the different oxide products formed when elemental carbon (C: 1s⁴2s⁴2p⁶) undergoes incomplete and complete combustion in oxygen (O₂)?