Four-Dimensional World Series

Four-Dimensional World (7): Electromagnetism

/** In this article, I plan to focus on physics in the four-dimensional world (four-dimensional space + one-dimensional time = five-dimensional spacetime) — specifically electromagnetism. These are theoretical derivations assuming this world also follows some of the physical laws from our world. Although electromagnetism is not as easily accepted as Newtonian mechanics, this analogy is flawless and very natural (or you can consider it all nonsense). We won't discuss quantum mechanics or other physics because their generalization to four-dimensional space has serious problems. **/

In our three-dimensional world, one of the most magical things is the electromagnetic field. Various electromagnetic induction phenomena are three-dimensional and require the right-hand rule in space. Can we analogize these things to four-dimensional space? Of course we can. Readers only need to have studied high school physics to read all content except the last section. If you know university physics and classical Maxwell’s equations without relativity, you can read the entire article (we only consider low-speed non-relativistic physical processes in four-dimensional space in this article, though relativity can actually be generalized to five-dimensional spacetime). Even if you’re not clear on these, it’s okay - I’ll guide you through a review first (physics review -_-). Let’s start with the simplest case: the force between two static charges separated by distance $r$.

Table of Contents

Electrostatic Fields

Electrostatic force is middle school knowledge: (Won’t half the readers disappear with multiple formulas? Well, there aren’t many readers anyway)

$$F={kQ_1Q_2\over r^2}$$
Like charges repel and opposite charges attract, and just like the law of universal gravitation, the electrostatic force between two point charges decreases with the inverse square of distance. However, in four-dimensional space, the inverse square law becomes an inverse cube law, which is a requirement of energy conservation. The reason starts with Gauss’s law. Electric field lines are actually similar to light rays: suppose we have a one-dimensional optical fiber with a light source at one end. If we don’t count energy loss, the other end can receive light signals of the same intensity, which is obvious. Now let’s make the optical fiber two-dimensional. Unlike the one-dimensional fiber, light from the source spreads in all directions. If we don’t count energy loss and we go around in a circle adding up all the light intensities, it equals the light source’s intensity. Since the light spreads out, the farther from the source, the sparser the light rays, and the lower the intensity. We consider concentric circles centered at the light source. Light rays pass through them sequentially, and the total flux of light rays is consistent, but larger circles have larger circumferences, which “dilute” the light rays. So light intensity is inversely proportional to circumference, and circumference is proportional to radius, so we can conclude that light intensity decreases with the inverse of distance.
Lossless optical cable (left) and sandwich plane with inverse distance attenuation (right)
In three-dimensional space, we consider concentric spheres centered at the light source. Similarly, we find that light intensity is inversely proportional to the sphere’s surface area, and surface area is proportional to the square of radius, so we can conclude that light intensity decreases with the inverse square of distance. Replacing light rays with electric fields gives us the attenuation law for electric fields. Naturally, in four-dimensional space, the light source can spread in even more directions. Considering concentric hyperspheres centered at the light source, we find that light intensity is inversely proportional to the hypersphere’s 3-volume, concluding that light intensity decreases with the inverse cube of distance. The electrostatic force formula between point charges becomes:
$$F={kQ_1Q_2\over r^3}$$
Actually, gravity follows the same pattern, as discussed when we talked about four-dimensional planetary orbits. Besides making orbits unstable in celestial mechanics, what else does the inverse cube law bring? It also makes electron orbits around atomic nuclei unstable. Although quantum mechanics doesn’t have classical orbits, the conclusion is the same. Using more “quantum” language, there are no stationary wave functions for electrons. So we can only assume that the microscopic theory of the four-dimensional world is completely different from ours and not discuss it to make our story consistent, otherwise the entire worldview of the four-dimensional world series would collapse. After all, my purpose is to construct a four-dimensional world as similar to our world as possible.

If we went to a four-dimensional world, what effect of the inverse cube law could we directly feel? Perhaps looking at the four-dimensional world’s sun or the streetlights in a four-dimensional city would be more dazzling, but not very bright… Also, sound propagation would be distorted, but I haven’t studied wave processes carefully yet.

/**Note that we assume Newton's three laws hold, meaning the unit of force is still $\mathrm{kg/(m/s^2)}$, this exponent doesn't become three. Do there exist worlds where the unit of force is $\mathrm{kg/(m/s^3)}$ or $\mathrm{kg/(m/s)}$? I've thought about it, those worlds are crazy! But they're unrelated to four dimensions so I'll discuss them separately later.**/

Electric Current

There’s actually not much to say about electric current because it doesn’t seem to be much affected by spatial dimensions. Current is the directional movement of charge, so it still equals the amount of charge passing through a unit cross-sectional cell (note that surfaces have upgraded to cells now) per unit time. It’s the flux of current density (note the units).

What we really care about is the magnetic effect of current. In three dimensions, the magnetic field of an infinite straight wire is concentric circles that decay inversely with distance. We can guess that the magnetic field of a four-dimensional wire should be concentric spheres decaying with inverse square, but it’s hard to imagine the direction of the magnetic field on the sphere surface. To know if we’re just guessing wildly, we first need to understand what a magnetic field is.

Steady Magnetic Fields

After learning about electric fields, it’s time to learn about magnetic fields. The simplest example we encounter in middle school is a bar magnet with north and south poles. We can also analogize to four-dimensional space, thinking that bar magnets also have magnetic field lines and north and south poles. But unfortunately, this conclusion is wrong. Because the origin of a magnet’s magnetic field is molecular current loops, i.e., current produces magnetic fields. But in the previous section, we only guessed that current’s magnetic field might have a spherical distribution. Let’s first recall the three-dimensional case: the relationship between the magnetic field direction at the center of a loop and the direction of the loop current follows the right-hand rule:

We should generalize this model to four dimensions. First ignoring what “right hand” means in four dimensions, the magnetic field direction at the center of the loop should be perpendicular to the plane of the loop current, but this direction is no longer unique in four-dimensional space (the normal space of a plane is also a plane, without a unique normal direction). This analogy leaves us unable to determine the magnetic field direction at the center of the loop, so this method doesn’t work. This is similar to our previous guess about the concentric spherical magnetic field of a current-carrying straight wire: the two-dimensional sphere surface also cannot give a specific direction.

Starting from Ampère Force and Lorentz Force

Let’s think differently about how magnetic fields are defined. High school physics defines the physical quantity “magnetic induction intensity” $B$, which is a vector, because current-carrying wires in magnetic fields experience a force we call “Ampère force”. Experiments show this force is perpendicular to both the magnetic field lines and the wire, and if the wire is parallel to the magnetic field lines, the Ampère force is zero. Mathematically, this relationship corresponds exactly to the cross product operation between vectors. For example, a wire along the x-axis in a y-axis magnetic field experiences a force along the z-axis.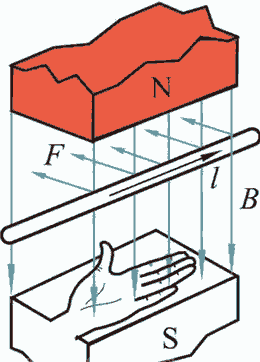

$$\boldsymbol{F}=I\boldsymbol{l}\times \boldsymbol{B}$$
If there were a two-dimensional world, would this world allow electromagnetic fields? If a current-carrying wire experiences a force perpendicular to both the current direction and magnetic field, that can only happen in at least three-dimensional space. But don’t we also say the rotation axis is perpendicular to a plane when we rotate a planar figure? This doesn’t mean only three-dimensional space can have rotation. Therefore, we should abandon specifying the so-called “perpendicular” direction, and instead specify the rotation axis as a rotation point and the magnetic field as a scalar, thus solving the problem.

Now in four dimensions, we assume the force is still perpendicular to both the magnetic field and the wire. What direction is the force on a wire along the x-axis in a y-axis magnetic field? It could be along the z-axis, w-axis, or a combination of both directions — we face the same problem as before. But we know that the direction of force must be definite, as is the direction of current, because they are both defined from object motion: force is related to the direction of object acceleration, and current is related to the motion of charges, so they must be vectors. On balance, we can only abandon the assumption that the magnetic field has a single direction. For example, if a wire placed along the x-axis experiences an induced force in the y direction, we directly consider the magnetic field to be in the zw direction. Another example: a wire in the x direction in a yz magnetic field experiences a force in the w direction. The inability to determine the magnetic field direction at the center of a loop current or around a current-carrying straight wire can all be explained: the magnetic field itself is two-dimensional, its direction is absolutely perpendicular to the plane of the coil. Perhaps you’ve already noticed, the magnetic field here is exactly the two-dimensional version of vectors I mentioned before — 2-vectors.

To be more specific: the magnetic field at the center of a loop current in the xy plane is in the zw direction. If you can’t imagine two-dimensional vectors, you can visualize the magnetic field as a vortex in the zw plane as shown below.
Uniform magnetic field in four-dimensional space
Note that 2-vectors (bivectors) here also have “positive and negative”, reflected in the direction of the vortex (although four dimensions cannot distinguish clockwise from counterclockwise, vortices still have direction), so the xy direction and yx direction are opposite (xy=-yx). The four-dimensional “right-hand” rule gives a coordinate arrangement order, and the specific operation is somewhat complex, involving even and odd permutations. This is the cross product operation between vectors and 2-vectors, so the high school Ampère force formula can be put into four-dimensional textbooks without any changes.

Let’s look at the essence: why do current-carrying wires experience Ampère force? High school physics tells us: charges moving in magnetic fields experience Lorentz force, which is the true source of Ampère force. Based on previous experience, we can directly write the expression for Lorentz force:$$\boldsymbol{F}=q\boldsymbol{v}\times \boldsymbol{B}$$

Since charges experience force in magnetic fields, our next step is to build a DC generator in four-dimensional space. Actually, its structure is the same as in three-dimensional space, just “thickened” in another direction, with magnetic field vectors also “thickened” into 2-vectors: like directly changing the x direction to the xw direction. Of course, are there better motor structures? For example, considering four-dimensional unique double rotation or Hopf fibration, would there be some special designs? I really can’t think of any now, it’s too abstract.

Magnetic Dipoles and Compasses

Torque on Current Loops

Now let’s analyze the deflection torque experienced by current loops in magnetic fields: In three-dimensional space, a magnetic dipole with magnetic moment $\boldsymbol{m}$ experiences torque $\boldsymbol{m}\times\boldsymbol{B}$ in magnetic field $\boldsymbol{B}$. What happens if we generalize this unchanged to four dimensions? First, the magnetic moment is defined as the normal to the plane of the loop current. This direction is two-dimensional in four dimensions, and the magnetic field is also two-dimensional. Cross-multiplying two 2-vectors will give a scalar, representing the volume of a parallel 8-cell (similar to the scalar triple product in three dimensions). But torque has direction and cannot be scalar, so the analogy fails. We’ll mention the reason for the failed analogy later. To analyze magnetic dipoles, we must work through current loops and cannot directly apply formulas.

We’ll only analyze a few special positions, then give the method for calculating torque without proof.

  • When the magnetic field is parallel to the coil, no point on the coil experiences force
  • When the magnetic field is absolutely perpendicular to the coil, the force on each point of the coil must be perpendicular to both the coil wire and magnetic field, so it can only be along the coil radius, causing the coil to tend to expand or contract but not rotate.
  • When the magnetic field is half parallel and half perpendicular to the coil (i.e., the dihedral angle is 90° as in three-dimensional space), the conclusion is that the coil experiences a net torque with a tendency to rotate in the direction of the magnetic field.

Let’s analyze the third case in detail: assume the coil is parallel to the xy plane and the magnetic field is parallel to the yz plane. The two A points in the diagram below have current parallel to the magnetic field and experience no force. Points B and C have opposite current directions, so one experiences force in the w direction, the other in the -w direction.

How does this force in the w direction make the coil rotate? Here are two methods to derive the rotation direction:

  1. Let’s calculate the torque: choosing the coil center as the point of action, B’s moment arm is along the y direction, B’s force is along the w direction. The three-dimensional torque is perpendicular to both, and generalizing to four dimensions, torque should also be perpendicular, so it’s in the xz direction. The torque direction is the axis of rotation, perpendicular to the rotation plane, so the effect of this torque is to make the coil rotate in the yw direction.
    If you’re careful, you’ll notice a problem: since B’s moment arm is along the y direction and B’s force is along the w direction, with the effect of making the coil rotate in the yw direction, why must we specify the torque as the xz direction perpendicular to them? Wouldn’t it be better to specify it directly as the yw direction? Indeed, this problem of flipping back and forth using perpendicular directions was also encountered when discussing magnetic fields in two-dimensional worlds. Three-dimensional space can represent planes with simpler normal vectors, so it uses the seemingly inexplicable direction perpendicular to the rotation plane as the torque direction. This also suggests that magnetic fields in three-dimensional space might be better defined as 2-vectors perpendicular to and of the same magnitude as the magnetic field vector, not only saving the tedious left and right-hand rules but also unifying the form of magnetic fields across different dimensions. For example, two-dimensional magnetic fields are not scalars but 2-vectors. This 2-vector can only be parallel to the plane of two-dimensional space, so it has only one component, feeling like a scalar. But to maintain consistency with high school physics knowledge, we still use the normal definition (actually a definition biased by three-dimensional thinking), using $\boldsymbol{B}^*$ to denote this better absolutely perpendicular definition.
  2. Directly draw the forces in xyw space and look with your eyes:
    Note that after replacing the z-axis with the w-axis, the magnetic field cannot be drawn
    Besides knowing that rotation occurs in the yw plane (or rotating around the xz-axis plane), we can also see that the coil tends to rotate toward the yw plane. As previously analyzed, the yw plane is absolutely perpendicular to the magnetic field, which is indeed an equilibrium position.

Cross Product Has More Than One Generalization

In summary, when the coil is parallel or absolutely perpendicular to the magnetic field, there is no torque; when half parallel and half perpendicular, there is torque. Although these are just a few special positions, according to the superposition principle, magnetic fields in any direction can be decomposed into six components in the coordinate system: $ae_{xy}+be_{xz}+ce_{xw}+de_{yz}+ee_{yw}+fe_{zw}$, where $e_{ij}$ represents unit 2-vectors. The inner product of two 2-vectors is non-zero only when components completely correspond, the outer product is non-zero only when components are completely different, and now there seems to be another operation that is non-zero only when components are not completely the same. This new operation feels between inner and outer products, which I’ll temporarily call the mixed product. Below I’ve organized a table:

Operation $e_{ij}*e_{ij}$ $e_{ij}*e_{jk}$ $e_{ij}*e_{kl}$
Inner product $\cdot$ 1 0 0
Outer product $\wedge$ 0 0 $e_{ijkl}$
Mixed product $\times$ 0 $e_{ik}$ 0

Note that the coil is parallel to the xy plane, the magnetic field is parallel to the yz plane, and the torque produces rotation in the yw plane. If we take the absolutely perpendicular direction xw of the magnetic field (the reason for taking this absolutely perpendicular direction is because of the previous description here) and do a mixed product with the coil plane xy, we get exactly the yw plane. Do you get a feeling: identical letters can merge and cancel, different letters are written together to form a multidimensional vector, and each dimension corresponds to a multiplication operation? Actually, they are all unified by something called Geometric Algebra! I’ll introduce it specifically when I have time.

Geomagnetic Field and Compasses

We’re now mainly concerned with what the geomagnetic field looks like and how compasses should work. The magnetic field of the three-dimensional Earth can be viewed as if there were giant current loops inside the Earth. The compass direction is actually just the component of the geomagnetic field on the horizontal plane; at the north and south poles, the geomagnetic field is almost vertical. We assume that four-dimensional planets also have internal current loops, but four-dimensional planets have double rotation. We have every reason to believe that there are two absolutely perpendicular current loops inside the planet, their directions roughly aligned with the two polar circles, but not completely coincident, just as the positions of magnetic poles on Earth deviate from geographic poles.

Let’s first assume there’s only a current loop in the xy plane. At this time, the magnetic field is strongest on the xy polar circle, completely horizontal. Its direction is the plane perpendicular to the polar circle direction (zw direction). Now we take a four-dimensional needle-shaped permanent magnet compass, with internal current loops producing magnetic fields. The compass experiences torque in the geomagnetic field and deflects. Can the needle deflect to point south? Of course, without considering resistance, the needle would oscillate back and forth due to energy conservation. Considering resistance, we also need to analyze the stability of equilibrium positions: for example, a three-dimensional compass pointing north is also an equilibrium position, but with a slight shake, it can return to the stable south-pointing equilibrium position.

For this, I wrote a program to calculate whether compasses at different initial angular positions can ultimately point south. What is the initial angular position here? Of course, it’s the angle between the current loop and the magnetic field. We already know that two planes need two angles to describe their positional relationship. But current loops and magnetic fields both have direction, suggesting that the range of angles can be larger than 0-90°. Analogous to how the angle between lines ranges from 0-90°, but the angle between vectors ranges from 0-180°. What’s the range of angles between two 2-vectors? The derivation is omitted here, just look at the conclusion below: The figure below marks the angles $\theta_1$ and $\theta_2$ between 2-vectors (taking $\theta_1\geq\theta_2$)

The origin O represents complete overlap with consistent direction, point D has one angle of 180°, representing overlap but opposite direction. Points A and B both have angles of 90°, both absolutely perpendicular, but point B has an angle of -90° because the directional order of the two 2-vectors is opposite to the right-hand rule (proper term: orientation). Line segment OA is left isoclinic planes with consistent direction, BD is left isoclinic planes with opposite direction, line segment OB is right isoclinic planes with consistent direction, AD is right isoclinic planes with opposite direction. The horizontal axis of the rhombus represents half-parallel, the vertical axis represents half-perpendicular. The center point C is half-parallel half-perpendicular.

This diagram shows all positional relationships, meaning each point corresponds to a relative orientation between the compass loop current and the geomagnetic field. Under magnetic torque, each point in the rhombus tends to move toward other points (i.e., we get a vector field). Programming can calculate the following figure:

We find that regardless of initial position, the final motion trend converges to the left vertex. Although the other three vertices are also equilibrium points, they are unstable - with slight disturbance, they move toward the left vertex. This demonstrates the stability of four-dimensional compasses.

But often four-dimensional planets have not just single rotation but also double rotation. The magnetic field might also be produced by two absolutely perpendicular current loops. This composite magnetic field has a characteristic: you can never determine the magnetic field direction by finding where wires don’t experience Ampère force. This magnetic field is similar to double rotation - it’s the superposition of two absolutely perpendicular vortices, therefore not a simple planar structure! You might say if multiple directional magnetic fields are superposed, wouldn’t the magnetic field structure be infinitely complex? Not so. It can be proven that any 2-vector can be decomposed into the sum of two absolutely perpendicular planar 2-vectors (for how to decompose specifically, see the orthogonal decomposition section in this article), so no matter how many magnetic fields are superposed, the complexity won’t exceed what we’re discussing here. When I set the magnetic field strength in the xy plane to be twice that in the zw plane, that vector field becomes:

You can clearly see that the absolutely perpendicular direction starts “stealing traffic”, but the zw plane magnetic field isn’t as strong as the xy plane’s, so it still can’t win, and ultimately the compass still points in the xy direction. What if the zw magnetic field were stronger or equal in strength? Below I’ve taken 0.9 times and equal cases respectively:
0.9 times (left); equal (right)
We find they become increasingly evenly matched, until finally when equal, the compass stops rotating once it reaches an isoclinic position. In this situation, the compass no longer has the function of pointing in a fixed direction. What’s going on? Actually, we’ve talked about the symmetry of isoclinic double rotation before: like the Hopf fibration, every great circle trajectory has the same status. On a planet with isoclinic double rotation, every point is no longer distinguishable, and the concept of north and south poles doesn’t exist. The failure of compasses on such planets is not surprising.

So what information can this compass give us on general non-isoclinic double-rotating planets? First, for Earth, magnetic fields are only parallel to the ground at the equator; elsewhere, the geomagnetic field is tilted, but as long as the compass is fixed horizontally, it can suppress the magnetic torque from the vertical component of the geomagnetic field. The four-dimensional case is the same, so the conclusion is: Four-dimensional compasses really are compasses that can point south like three-dimensional compasses, because the current loop will match the two-dimensional component obtained by projecting the magnetic field onto the three-dimensional ground. The normal to the current loop can be uniquely determined on the three-dimensional ground - this is south, but it doesn’t provide other additional information besides pointing south. (Update 2022.10.16) The previous conclusion is wrong. A compass constructed this way will point east, not south. Details will be in the next update. For the three-dimensional world, giving one direction is sufficient, but for four-dimensional people, it’s not enough. Remember that rotation method that can spin while maintaining forward direction? Four-dimensional people need one more direction to fully know their orientation on three-dimensional ground. (Think about how an airplane’s attitude includes not just horizontal direction but also roll angle) So navigation in the four-dimensional world is indeed very difficult. You can imagine the mortality rate of explorers in this world must be very high.

Four-Dimensional Maxwell’s Equations?

If you’re completely unfamiliar with university physics, please skip this section or come back after reading relevant books.

Ampère’s Circuital Law

Ampère’s circuital law describes how current produces magnetic fields. It’s generally given in the form of a path integral:
$$\oint_l\boldsymbol{B}\cdot \boldsymbol{dl}=\mu_0 (\boldsymbol{I}+\iint_D \epsilon_0\frac{\partial \boldsymbol{E}}{\partial t}\cdot \boldsymbol{dn}) $$
where the second term on the right is displacement current (changing electric fields look like a kind of current density because they also produce magnetic fields; the flux of changing electric fields through a cross-section is called displacement current). Its value is calculated by choosing any two-dimensional region $D$ with path $l$ as its boundary, where $n$ is the normal to area elements of region $D$. (i.e., $\boldsymbol{dn}=\boldsymbol{dS}^*$. Here the asterisk is the Hodge dual, which turns area elements into normals, i.e., a kind of flux.)

What about the two-dimensional case? We only need two points to “surround” a wire: (see the left side of the three figures below)
Note that you absolutely cannot interpret the dots and crosses in the figure as pointing out of or into the paper, because the two-dimensional world doesn’t have this direction. They only represent the positive and negative signs of the scalar magnetic field.
The so-called circulation simply becomes the difference between magnetic field values at two points, and the surface bounded by the loop becomes a curve:
$$\boldsymbol{B}(A)-\boldsymbol{B}(B)=\mu_0 (\boldsymbol{I}+\int_D \epsilon_0\frac{\partial \boldsymbol{E}}{\partial t}\cdot \boldsymbol{dn}) $$
This shows that the magnetic field of a two-dimensional infinite wire doesn’t decay! But infinite wires don’t exist anyway, so two-dimensional electromagnetism is still “well-behaved”.
Generalized Ampère's circuital law from two to three to four dimensions
Extending to four dimensions, one-dimensional loops can no longer wrap around one-dimensional wires (refer to the article Four-Dimensional Space (10): Knots and Links), so path integrals must be upgraded to surface integrals. Also, magnetic fields are two-dimensional, so surfaces can match with equally two-dimensional magnetic fields to compute inner products, because integrals ultimately calculate scalars. In surface integration, each area element is a small 2-vector that takes an inner product with the magnetic field to get a scalar. This scalar accumulates over the entire surface to get a kind of two-dimensional “circulation”, and the flux value is proportional to the current enclosed by the surface.
$$\oint_S\boldsymbol{B}\cdot \boldsymbol{dS}=\mu_0 (\boldsymbol{I}+\iiint_D \epsilon_0\frac{\partial \boldsymbol{E}}{\partial t}\cdot \boldsymbol{dn})$$

Faraday’s Law of Electromagnetic Induction

Faraday’s law of electromagnetic induction describes how changing magnetic flux induces electromotive force in loops:
$$\oint_l\boldsymbol{E}\cdot \boldsymbol{dl}=-\iint_D \frac{\partial \boldsymbol{B}}{\partial t}\cdot \boldsymbol{dn} $$
In the two-dimensional case, scalar magnetic fields have no concept of flux, but if understood as magnetic fields perpendicular to the two-dimensional plane, we should directly integrate the scalar to get flux:
$$\oint_l\boldsymbol{E}\cdot \boldsymbol{dl}=-\iint_D \frac{\partial B}{\partial t}\cdot dxdy $$
As we analyzed before, wires are one-dimensional, loop boundaries are also one-dimensional. In four dimensions, flux passes through 3-cells, and the boundary of a 3-cell is a closed surface, not a closed curve like a loop. This seems contradictory but actually isn’t.
In three-dimensional space: vectors pass perpendicularly through surfaces, 2-vectors pass perpendicularly through curves
Flux is for vector fields, but the conclusion is different when analogized to 2-vectors. The most intuitive feeling is: ordinary 1-vectors are one-dimensional, so in three-dimensional space they need to pass through two-dimensional surfaces, and in four-dimensional space through three-dimensional surfaces; 2-vectors are themselves two-dimensional, so they only need to pass through curves in three-dimensional space and through two-dimensional surfaces in four-dimensional space. Let’s directly use $\boldsymbol{B}^*$ to rewrite Faraday’s law of electromagnetic induction, saving the need to calculate flux and take another normal:
$$\oint_l\boldsymbol{E}\cdot \boldsymbol{dl}=-\iint_D \frac{\partial \boldsymbol{B}^*}{\partial t}\cdot \boldsymbol{dS} $$
Now this formula defined with $\boldsymbol{B}^*$ is already applicable to four dimensions, and even two dimensions.

Gauss’s Law

The other two equations in Maxwell’s equations are much simpler. First, magnetic fields have no divergence, meaning the flux integral over any closed surface is zero.
$$\oint_S\boldsymbol{B}\cdot\boldsymbol{dn}=0$$
First, two-dimensional magnetic fields are scalars, and scalars have no divergence, always zero, so no equation is needed.
In four dimensions, it should be the flux integral over any closed 3-cell equals zero, but as analyzed before, the flux of two-dimensional magnetic fields is measured by two-dimensional closed surfaces, so the equation should be:
$$\oint_S\boldsymbol{B}\cdot\boldsymbol{dS}^*=0$$
Note that $dS^*$ above should be understood as the normal (absolutely perpendicular) area element to the corresponding area element $dS$, so the calculation gives flux. Or we can directly consider the magnetic field $B$ uses the absolutely perpendicular new definition $\boldsymbol{B}^*$, then we don’t need normal area elements and it applies to spaces of all dimensions:
$$\oint_S\boldsymbol{B}^*\cdot\boldsymbol{dS}=0$$
But in two-dimensional space, it’s impossible to construct two-dimensional closed surfaces, so the Gauss’s law equation for two-dimensional magnetic fields doesn’t need to be written, consistent with the previous statement that scalars have no divergence.
For electric fields, it’s even simpler:
$$\epsilon_0\oint_S\boldsymbol{E}\cdot\boldsymbol{dn}=q$$
Electric fields are ordinary vectors, so just replace the closed surface $S$ with closed 3-cell $V$:
$$\epsilon_0\oint_V\boldsymbol{E}\cdot\boldsymbol{dn}=q$$

Four-Dimensional Electromagnetic Waves

Can four-dimensional electromagnetic fields mutually excite each other to form electromagnetic waves? We first need to write the above integral equations in differential form. First define the derivative operator $$\boldsymbol{d}=\frac{\partial}{\partial x}\boldsymbol{e}_x+\frac{\partial}{\partial y}\boldsymbol{e}_y+\frac{\partial}{\partial z}\boldsymbol{e}z+\frac{\partial}{\partial w}\boldsymbol{e}w$$ This is the gradient operator from calculus. If $f$ is a scalar field, then $\boldsymbol{d}f=\text{grad}(f)$. If $f$ is a vector field, then $(\boldsymbol{d}\wedge f)^*=\boldsymbol{d}\times f=\text{curl}(f)$, $(\boldsymbol{d}\cdot f)=(\boldsymbol{d}\wedge f^*)^*=\text{div}(f)$.
This way we’ve generalized gradient, divergence, and curl.
To eliminate the integral sign, we also need to use the Stokes formula on manifolds:
$$\oint{\partial} \omega=\int{i}\boldsymbol{d}\wedge \omega$$
where the left side integrates an n-vector over the n-dimensional closed surface of an (n+1)-dimensional region, equaling the right side’s direct integration in the (n+1)-dimensional region after applying the derivative operator. (For brevity, the formula omits dot products with corresponding area and volume elements under the integral sign)
How do we understand this formula? $\boldsymbol{d}\wedge$ is similar to cross product, so it’s a kind of generalized curl. The left side is the “circulation” of n-vectors on the boundary of a closed region, while the right side is the total contribution of all n-vector curls inside the region. Yes, those who’ve studied multivariable calculus can see this is a generalization of the three-dimensional Stokes formula.

  • First let’s write the differential form of Gauss’s law for electromagnetic fields:
  • $\boldsymbol{d}\boldsymbol{B}^*=(\boldsymbol{d}\boldsymbol{B}^*)^*=0$, the divergence of magnetic field $B$ is 0, making it a sourceless field.
  • $\epsilon_0(\boldsymbol{d}\boldsymbol{E}^*)^*=\rho$, electric field divergence equals charge density.
  • Then the mutual excitation of changing electromagnetic fields:
  • $(\boldsymbol{d}\wedge\boldsymbol{E})^*=-\frac{\partial \boldsymbol{B}}{\partial t}$
  • $(\boldsymbol{d}\wedge\boldsymbol{B})^*=\mu_0(\boldsymbol{j}+\epsilon_0\frac{\partial \boldsymbol{E}}{\partial t})$

Assuming there’s no current density $\boldsymbol{j}$ or charge density $\rho$ in space, we apply $(\boldsymbol{d}\wedge)^*$ to both sides of the equation $(\boldsymbol{d}\wedge\boldsymbol{E})^*=-\frac{\partial \boldsymbol{B}}{\partial t}$ to eliminate the magnetic field, getting:
$$(\boldsymbol{d}\wedge(\boldsymbol{d}\wedge\boldsymbol{E})^*)^*=-\mu_0\epsilon_0\frac{\partial^2 \boldsymbol{E}}{\partial t^2}$$
What’s that chunk on the left? We can expand it directly in coordinates. After lengthy calculation, we have
$$(\boldsymbol{d}\wedge(\boldsymbol{d}\wedge \boldsymbol{E})^*)^*= -\boldsymbol{\Delta E}+\text{grad}(\text{div}(\boldsymbol{E}))$$, exactly the same as the three-dimensional case. Since there’s no charge $\rho$, the right term is 0, and we finally get the standard wave equation:
$$\boldsymbol{\Delta E}-\mu_0\epsilon_0\frac{\partial^2 \boldsymbol{E}}{\partial t^2}=0$$
Similarly eliminating the electric field and using zero magnetic field divergence gives:
$$\boldsymbol{\Delta B}-\mu_0\epsilon_0\frac{\partial^2 \boldsymbol{B}}{\partial t^2}=0$$
where $\boldsymbol{\Delta B}$ is the 2-vector Laplace operator, which like vectors acts directly on each component of the 2-vector.

It’s easy to see the vacuum speed of light $c={1 \over \sqrt{\mu_0\epsilon_0}}$. Since the speed of light doesn’t change with reference frame, can this open the door to five-dimensional spacetime special relativity?

Four-Dimensional Wave Optics

Let’s assume there’s a uniform hyper-cell electromagnetic wave (upgrade of plane wave!) propagating in the x-axis direction and see what happens.

  • Assume the electric field has only an $x$ component. Then the electric field curl is zero, and no magnetic field can excite this kind of electric field.
  • Assume the electric field has only a $y$ component. Then the electric field curl vortex direction is xy, and if there’s a zw-direction magnetic field changing sinusoidally, it might excite this electric field, also changing at the same frequency and phase.
  • Assume the magnetic field has only an $xy$ component. Then the magnetic field curl is zero, and no electric field can excite this magnetic field.
  • Assume the magnetic field has only a $yz$ component. Then the magnetic field curl is w, and if there’s an electric field in the w direction changing sinusoidally, it can excite this magnetic field, also changing at the same frequency and phase.

From the somewhat informal description above, we can see that in four-dimensional space, the propagation direction and electromagnetic fields are still mutually perpendicular. So we can look at polarized light in four-dimensional space. We know polarized light can be classified as linear polarization, elliptical polarization, circular polarization, etc. Although three directions of same-frequency sinusoidal electric fields can all participate in synthesis, they won’t produce more three-dimensional figures. In the three-dimensional wave front cell, they can still only synthesize lines, ellipses, and circles. Since determining the electric field also determines the magnetic field, there aren’t many polarization modes for four-dimensional electromagnetic waves. We can also calculate reflection/refraction coefficients for different polarized light like in three dimensions, i.e., the 4D version of Fresnel formulas! Based on whether electric and magnetic fields are parallel to the interface, there are still two Fresnel formulas. I don’t want to calculate the specifics unless I need to develop a 4D physical ray-tracing rendering engine in the future.