// Note: This article involves 4D planetary direction positioning based on Hopf polar coordinates. Please first read Four-Dimensional World (I): Day, Night and Seasons on Planets to understand the most basic directional terminology on 4D planets.
Previously in “Four-Dimensional World (VII): Electromagnetism,” I mentioned how to use the geomagnetic field of a 4D planet for navigation, but didn’t specifically analyze how to design and use compasses. This article will supplement this content, providing a correct directional identification guide for explorers on 4D planets using magnetic fields, Coriolis force, and the starry sky.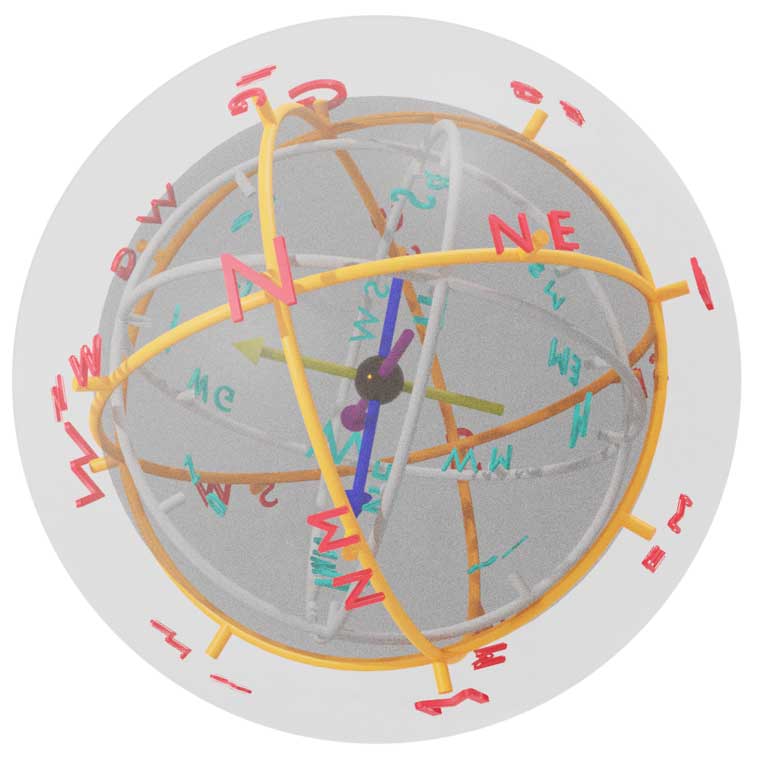
How to Design a Compass
Navigation shouldn’t really be a problem for modern 4D people. They should have long mastered the technology to manufacture gyroscopes - these devices that maintain their orientation based on conservation of angular momentum won’t fail on isoclinic double-rotating planets that lack distinct north and south poles. Gyroscopes can even be analogized for use on planets in arbitrarily high-dimensional universes. However, manufacturing such precision instruments isn’t something a primitive civilization can do right away, so let’s look at how to make a compass using magnets and the geomagnetic field. To design a properly functioning compass, we need to consider at least these issues:
- Determine the mechanical structure of the compass, including magnetization direction, installation method, and how to fix it in the 3D dial;
- Since the compass rotation is restricted by the dial to a 3D subspace parallel to the ground, we need to understand which components of the external magnetic field contribute to the compass deflection;
- What is the direction of the geomagnetic field at various locations on the planet;
- Under what circumstances will the compass fail
First, we need to determine the mechanical structure of the needle and dial. Since the needle needs to point to any position on the 3D ground, this symmetry requires the dial to be a kind of “spherical disk,” i.e., a very thin spherical cylinder shape, which should also have a transparent shell layer to enclose the needle. How is the needle fixed on the dial? Like in the 3D world, we can leave a spherical hole in the middle of the magnetic needle and thread it onto a 1D axis in the center of the dial. After using some techniques to reduce shaft friction, this compass can approximately rotate completely freely in 3D space.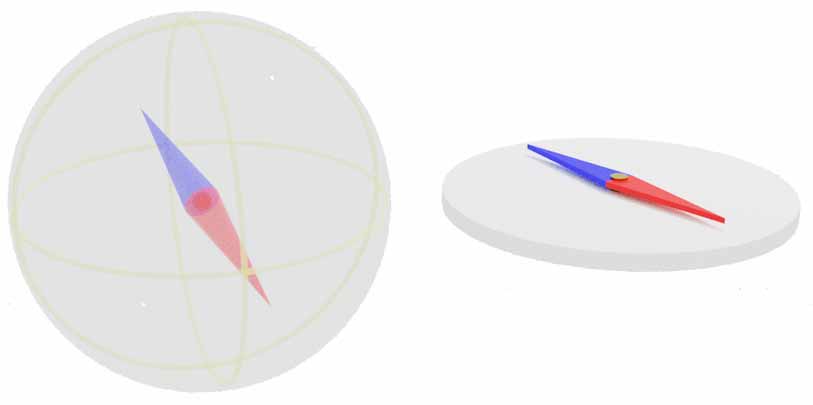
Magnetization Methods for Compasses
Next, we need to magnetize the needle so it can be deflected by force in the geomagnetic field. Since in 4D space, the traditional concept of magnetic poles must be abandoned, we can only speak of the vortex direction of loop currents, rather than continuing to use familiar concepts like “north and south poles” or “magnetic field lines.” In 3D space, these two methods of representing magnetic fields are perpendicular to each other, with specific directions determined by the right-hand rule. For example, the following figure shows the magnetic field distributions of a current-carrying straight wire and a loop current coil.
We see that the magnetic field vortex direction around a current element is like the vortex direction of surrounding fluid driven by a charge moving through it. The magnetic field vortex inside the loop current is in the same direction as the loop current, while outside it’s opposite. How does a compass work in 3D space? The distribution of Earth’s internal geomagnetic field is actually very complex, generally replaced by an idealized magnetic dipole (i.e., a small-sized loop current) model located at the Earth’s center (red circle in the figure below). The loop current vortex direction of the compass needle is perpendicular to the needle direction. Under the action of an external magnetic field, the needle experiences a torque and deflects, eventually rotating to an equilibrium position—where the needle aligns with the magnetic field lines, or where the loop current aligns with the magnetic field vortex. When the magnetic needle points north-south at equilibrium, the current vortex direction is parallel to the equatorial plane, i.e., the plane spanned by the east-west direction and the vertical direction. Note that at the north and south poles, the magnetic field lines are perpendicular to the ground, and the magnetic field vortex is completely parallel to the ground, causing the compass to fail (without horizontal dial restriction, it would point up or down).
(Side note: The N/S marked in the figure are the geomagnetic south and north poles, which are opposite to the geographic poles. Why are they opposite? We define the magnetic pole on a magnet that points north (geographically) as the north pole. However, like poles repel and opposite poles attract, so for Earth as a large magnet, the magnetic pole that can attract the north pole should be the south pole (geomagnetically).)
How do we magnetize a 4D compass? Following the 3D analogy, we can construct such a compass: Just like the analysis in 3D space, the magnetic needle will deflect to a direction where its loop current vortex orientation is consistent with the external magnetic field vortex (we’ll analyze the effect of dial and axis restrictions later). For simplicity, assume the explorer is on the east-west equator (remember there’s also a yin-yang equator on the other side of the 4D planet!). Here the magnetic field vortex direction is parallel to the equatorial plane, and the explorer experiences a geomagnetic field vortex in the plane spanned by the east-west direction and vertical direction. The side of the magnetic needle naturally aligns with the east-west direction. After alignment, unlike the 3D case where the needle always points south, the needle can rotate freely in the plane perpendicular to the east-west direction on the ground, because it’s absolutely perpendicular to the equatorial plane, and rotation doesn’t affect the magnetic field alignment. That is, after this compass’s side points east, it doesn’t matter where the needle actually points—it’s more like a “point-east compass”! Why did our analogized south-pointing compass become east-pointing? Looking at the figure below reveals: There’s actually no essential difference between south-pointing and east-pointing compasses on Earth, just different needle shapes during manufacturing. Their difference only becomes apparent in 4D! Since that’s the case, let’s directly align the loop current with the needle to make a point-east compass.
Are there other magnetization methods? By symmetry, there’s no difference in status between the east-west direction and the yin-yang direction (i.e., the directions of two absolutely perpendicular loop currents). Perhaps we can make a “point-yang compass,” and with both east-west and yin-yang directions determined, the remaining south-north direction perpendicular to them can also be determined! How do we make a point-yang compass? We see that the loop current of the point-east compass lies in a 2D plane perpendicular to the 3D ground, so naturally another approach would be to have the loop current completely within the ground plane. The figure below shows both magnetization methods. Note that these two magnetization directions are absolutely perpendicular, so they cannot be drawn in the same 3D view. (The point-east compass is shown in side view while the point-yang compass is shown in top view)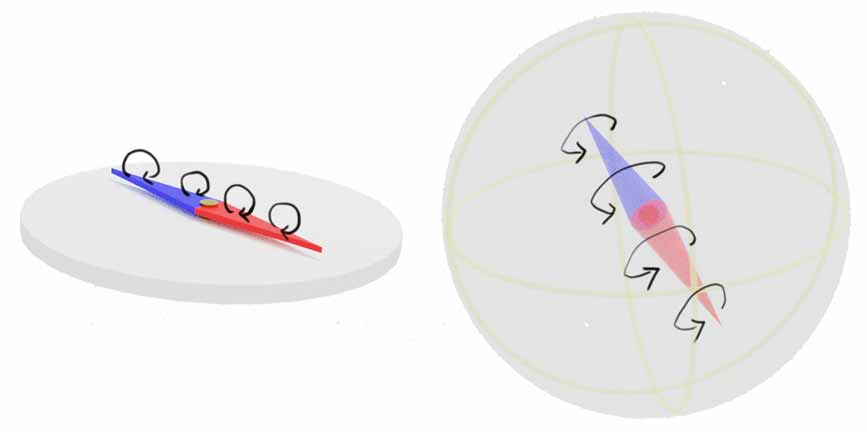
Will these two types of needles really point to the east-west and yin-yang directions respectively everywhere on the planet? Hold on, let’s first look at the forces and deflection of the two types of compasses in magnetic fields. The point-east compass has a vertical vortex magnetic field; it will rotate horizontally to match the vertical component of the geomagnetic field, ignoring the horizontal component. Similarly, the point-yang compass has a vortex magnetic field parallel to the ground; it will rotate horizontally to match the horizontal component of the geomagnetic field, ignoring the vertical component.
Is the matching theory really true in “fact”? Readers who aren’t interested please skip to the next section. Previously when introducing 4D electromagnetism, I analyzed through computational simulation the stability of equilibrium positions when a 4D magnetic dipole deflects in an external magnetic field. I found that only when the magnetic dipole orientation is consistent with the external magnetic field vortex is it a stable equilibrium position. Therefore, the vortex matching theory is reliable. However, at that time I didn’t consider the dial’s restriction on vertical rotation, so we still need to orthogonally decompose the magnetic field for force analysis: In 4D space, torque is a 2-vector, such as $e_{xy}$ representing a unit-sized torque with rotation direction from the positive x-axis to the positive y-axis. Decomposing any 2-vector in a Cartesian coordinate system gives us 6 components: $e_{xy},e_{xz},e_{xw},e_{yz},e_{yw},e_{zw}$. Let the w-axis be the vertical direction, then torques containing w direction like $e_{xw},e_{yw},e_{zw}$ will make the needle deflect up and down, but due to the central axis fixation, the needle cannot rotate; the remaining three directions $e_{xy},e_{xz},e_{yz}$ all fall within the 3D ground space, exactly the degrees of freedom for the compass’s free rotation. Next, let’s look at the magnetic field that produces torque. Due to dial restrictions, not all magnetic field components contribute to the torque that can cause needle deflection. Here we need to discuss the two magnetization directions separately. I analyzed here the calculation method for the torque experienced by a magnetic dipole in a magnetic field, which is a cross product operation between inner and outer products.
- “Point-east compass”: The needle is always restricted to the horizontal direction, and the loop current vortex direction must be in a plane spanned by some ground direction and the vertical direction, i.e., the needle’s magnetic moment orientation can only be a combination of $e_{xw},e_{yw},e_{zw}$. According to cross product rules, when they cross with horizontal magnetic field components $e_{xy},e_{xz},e_{yz}$, the non-zero components obtained must contain the letter w, i.e., they’re all the kind of up-down rotation restricted by the central axis, so only the magnetic field vortex component perpendicular to the ground can make this compass deflect.
- “Point-yang compass”: The magnetization direction is absolutely perpendicular, exactly opposite to the above. The needle’s loop current magnetic dipole moment orientation can only be a combination of $e_{xy},e_{xz},e_{yz}$. When they cross with magnetic fields in the $e_{xw},e_{yw},e_{zw}$ directions, they all produce the kind of up-down rotation restricted by the central axis. Therefore, for this type of compass, we only need to care about the magnetic field components on the horizontal ground.
Distribution Pattern of the Geomagnetic Field
Now we’ve figured out the compass’s magnetization direction and how it deflects in an external magnetic field, but what should the direction of the external magnetic field (i.e., geomagnetic field) be? This article ignores the error between magnetic poles and rotational geographic poles, assuming geographic south-north poles coincide with geomagnetic south-north poles, so the following text doesn’t distinguish between geographic and geomagnetic poles. From the Earth’s magnetic field distribution earlier, we can find that the distribution pattern of magnetic field components parallel to the ground on a spherical surface is strong at the equator and weak at the poles, while components perpendicular to the ground are weak at the equator and strong at the poles. Note that vortices are perpendicular to the usual magnetic field direction (i.e., magnetic field lines), so when describing vortices, the horizontal and vertical variation patterns are exactly swapped: The distribution pattern of magnetic field vortex components perpendicular to the ground on a spherical surface is strong at the equator and weak at the poles, while components parallel to the ground are weak at the equator and strong at the poles. Analogizing to 4D, if the magnetic dipole current direction is still east-west, then going from the east-west equator toward high latitudes of the south-north equator, the component perpendicular to the ground gradually weakens to zero, while the component parallel to the ground does the opposite, gradually strengthening from zero; if the magnetic dipole current direction is yin-yang, then the entire pattern reverses: going from the east-west equator toward high latitudes of the south-north equator, the component perpendicular to the ground gradually strengthens from zero, while the component parallel to the ground gradually weakens to zero. Let’s summarize with a table:
| Field Source Direction | Component | East-West Equator | Mid-latitude | Yin-Yang Equator |
|---|---|---|---|---|
| East-West | Vertical | Strongest | Weakening | Zero |
| East-West | Horizontal | Zero | Strengthening | Strongest |
| Yin-Yang | Vertical | Zero | Strengthening | Strongest |
| Yin-Yang | Horizontal | Strongest | Weakening | Zero |
Assuming this planet only has loop currents in the east-west direction internally, let’s see how these two compasses point at various latitudes on the planet. First, our explorer starts from the south pole—on the east-west equator, heading to the north pole—the yin-yang equator. On the east-west equator, the point-east compass senses the vortex spanned by the vertical direction and east-west direction, thus deflecting to point east. At this time, the point-yang compass doesn’t experience any horizontal torque and is in a failed state, which is actually the same as a compass failing at the north and south poles on Earth. Near the east-west equator, the yin-yang direction forms increasingly smaller circles (yellow in the figure below, analogous to latitude circles near the north pole), so it’s quite normal for the point-yang compass to fail here.
The explorer departs in any direction perpendicular to the east-west equator heading north (the equator is already the southernmost point) and arrives at mid-latitude regions. Here the geomagnetic field is tilted, having both horizontal and vertical components. At this time, both the point-east and point-yang compasses work properly, and the explorer can completely determine their orientation through them. Finally, they arrive at the north pole—the yin-yang equator. Here the point-east compass fails, while the point-yang compass works normally.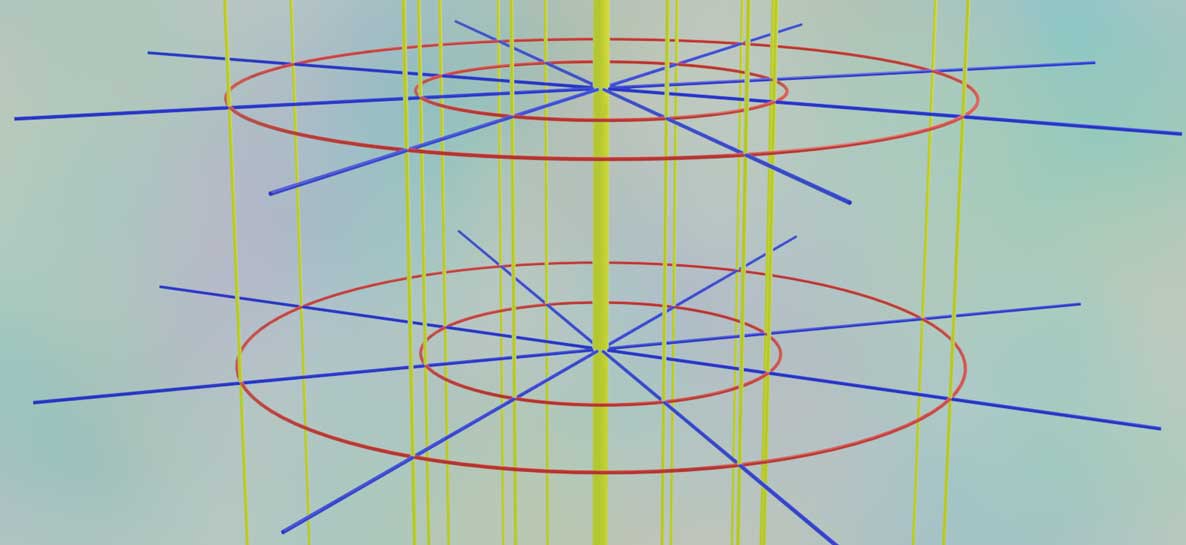
As long as you’re not exactly on the equator, the east-west, yin-yang, and south-north directions are definitely perpendicular. This inspires us to directly weld the two types of compasses together to rotate as one, or simply make a spherical compass with both magnetization directions, directly marking all six directions—east, west, south, north, yin, and yang! Note that originally if two needles point in the same direction, their magnetization directions are absolutely perpendicular. However, now they’re at a 90-degree angle, so the two magnetic fields the compass possesses are actually semi-parallel and semi-perpendicular. Therefore, after superposition, the compass’s magnetic moment isn’t a compound magnetic field, but a simple vortex magnetic field at a 45-degree angle to the horizontal plane—we can better understand this superposition through normal vectors. (Note: In 4D space, only 2-vector vortices of two co-3D spaces (semi-parallel) can be marked with normals and added to get a new simple vortex with a single direction. Non-semi-parallel 2-vector superposition results in compound 2-vector vortices—these 2-vectors can be represented by the superposition of at most two absolutely perpendicular vortices no matter how many times they’re superposed)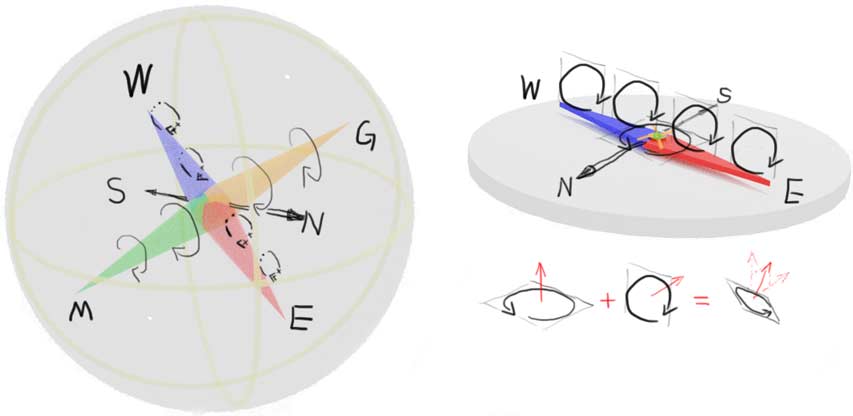
Thus, we’ve combined two compasses into one. The analogized compass is very perfect! Except at the south-north pole equators, explorers can precisely align east-west-south-north-yin-yang with just one 3D compass!
Simulation of 4D Planetary Geomagnetic Field and Compass
I’ve created an interactive 4D planetary scene where you can dynamically observe the sun’s movement patterns on this planet while navigating with a compass:
- Click here to run
- If it doesn’t open, please refer to this tutorial.
This planet only has a loop current geomagnetic field in the short-day equator direction. According to “Four-Dimensional World (I): Day, Night and Seasons on Planets,” on the two equators you’ll only experience long-day and short-day time variations respectively, while mid-latitude regions experience a superposition of both periods. Therefore, we can first judge whether we’ve reached the polar regions through the solar altitude curve, and second, we can judge based on the compass orientation. If you’re clear on all concepts and operations, you’ll find these two criteria are consistent in the simulation—the compass indeed works completely correctly as we expected!
4D Planet Feature: Compound Geomagnetic Fields
However, as the old saying goes, there’s no such thing as perfection in the world. We can guess that the magnetic dipole at the center of a 4D planet might have more or less some compound magnetic moment—i.e., loop currents not only in the east-west equator direction, but also weaker loop currents in the absolutely perpendicular yin-yang equator direction. Can our point-east compass, point-yang compass, or this compound dual compass work as expected under a compound geomagnetic field? Spoiler alert: Unfortunately, no.
A simple (non-compound) geomagnetic dipole can be considered directly analogized from 3D. However, if the magnetic field is compound, the equilibrium position of the needle here isn’t so intuitive. But we can decompose the compound field into the superposition of two absolutely perpendicular simple magnetic fields, and the force experienced by the needle can also be decomposed into the forces experienced in these two magnetic fields separately.
Our explorer comes to another 4D planet where the geomagnetic dipole’s loop current in the yin-yang direction is one-third that in the east-west direction. The explorer now stands on the south pole equator. The east-west direction loop current only produces magnetic field perpendicular to the ground here, while the yin-yang direction loop current only produces magnetic field parallel to the ground. Therefore, both the point-east and point-yang compasses in their hands can work simultaneously! Where will the previously failing point-yang compass in a simple magnetic field now point? The answer is it will also point to the east-west direction! This is actually easy to understand: It’s not hard to see that regardless of the geomagnetic loop current direction, a needle made with the point-east magnetization method will tend to point in the direction of the loop current, while a needle made with the point-yang magnetization method points perpendicular to the loop current and perpendicular to south-north. Unlike the east-west direction, the yin-yang direction’s “point-east compass” now becomes a “point-yang compass,” and the “point-yang compass” becomes a “point-east compass,” so they both point east! We summarize a table listing the force situations in all cases at all locations:
| Needle Type | Geomagnetic Direction | East-West Equator | Mid-latitude | Yin-Yang Equator |
|---|---|---|---|---|
| Point-East | East-West | Strongest | Weakening | Failed |
| Point-East | Yin-Yang | Failed | Strengthening | Strongest |
| Point-Yang | East-West | Failed | Strengthening | Strongest |
| Point-Yang | Yin-Yang | Strongest | Weakening | Failed |
Actually, without analyzing any specific deflection direction, we can reach a conclusion through symmetry—the magnetic field is completely symmetric along directions perpendicular to the equator. Apart from pointing east, you can’t expect any geomagnetic sensing instrument to distinguish other directions, because just like at Earth’s south pole, every direction is north. At the pole, the east-west direction has lost its meaning.
The explorer continues north. As they go north, the two needles in their hands start from both pointing east-west, then the angle between them slowly increases. Continuing north, the angle slowly decreases again. When they reach the yin-yang equator at the north pole, the two needles have completely overlapped, both pointing in the yin-yang direction. You can see the complexity of compass navigation on a planet with compound magnetic fields! Why is this? For compound fields, each type of needle will point to a new equilibrium position under the superposition of two forces. This position often doesn’t coincide with either magnetic field—it’s the result of balanced competition between both sides. This vector addition following the parallelogram rule isn’t friendly to maintaining angles. Computer calculations show that while they’ll still be perpendicular to the south-north direction, the angle between these two types of needles isn’t perpendicular, and they both have angles with the east-west and yin-yang directions. Moreover, the angles continuously change with latitude, which is very troublesome: Imagine 4D explorers having to recalibrate their compasses at different latitudes, and they also need to know how to calculate these deviation angles or look them up in pre-calculated tables!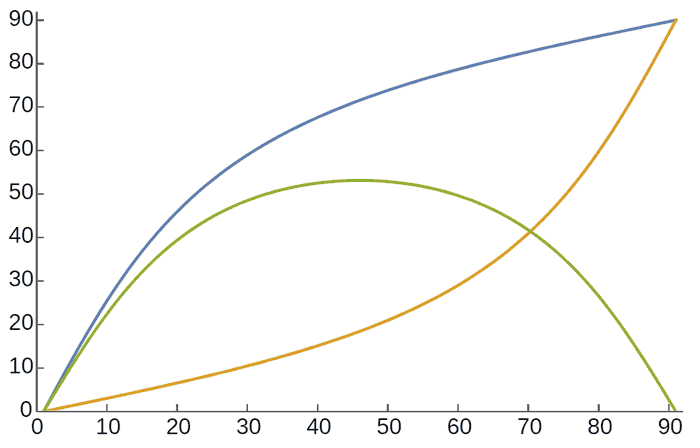
Looking at two compasses simultaneously is too troublesome. If we still make both magnetization directions into one spherical compass like the single-rotation planet’s compass, carefully controlling the ratio of horizontal to vertical magnetization strength, we might be able to give explorers the correct orientation. Calculations show that carefully controlling the magnetization strength ratio can indeed correct the deviation, allowing the spherical compass to realign with the east-west and yin-yang directions. However, the ratio for controlling magnetization strength needs to change at different latitudes, so you might need to buy some “local compasses” that can only be used near regions of the same latitude. If explorers want to travel around the world, the universal compass they need would still be two needles. First, the direction perpendicular to both needles is south-north, and according to the right-hand rule, you can determine which is south and which is north. Knowing the east-west and yin-yang directions is more troublesome: First read the angle between the two needles, look up the table to get your latitude. There’s another difficulty in this step—from the curve earlier, we know that generally one angle corresponds to two latitudes. At this time, explorers need to judge high or low latitude themselves, which is both difficult near curve extrema and has large errors in latitude determination. Finally, use the latitude to look up the table to correct your compass deviation. You can imagine that “local compasses” are convenient to use, suitable for non-professionals exploring in small areas; universal compasses require looking at two needles and table corrections, have a high learning curve, but are the best choice for experienced explorers. If 4D planetary civilization’s technology advances, it’s not impossible to automatically adjust the compass’s magnetization ratio based on the angle between two needles through mechanical/electronic devices, thus having a foolproof universal compass (provided the difficulty of determining latitude is solved). (Since technology is advanced, why not just use gyroscopes and satellite positioning navigation?)
If the yin-yang direction loop current is very small compared to the east-west direction, then we can predict that a compass integrating point-east and point-yang needles should barely work. The figure below shows the needle angle variation curve when the geomagnetic dipole’s yin-yang direction loop current is one percent of the east-west direction: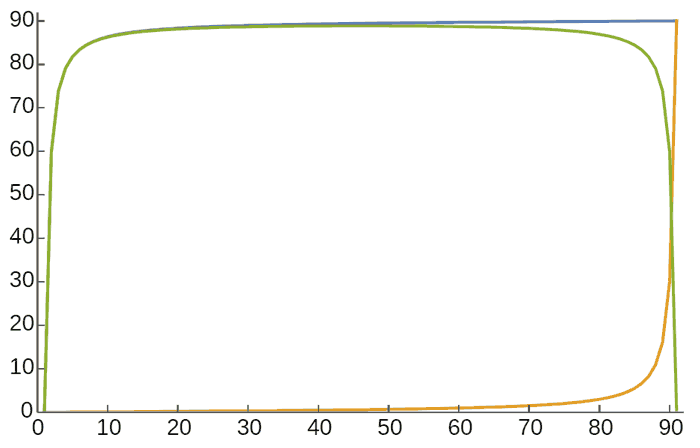
Now let’s look at an extreme case: self-dual magnetic dipole—a dipole similar to isoclinic double rotation with equal east-west and yin-yang loop current strengths. Like isoclinic double rotation, this type of dipole is highly symmetric and can have many ways of decomposing loop currents (refer to orthogonal decomposition in “Four-Dimensional Space (VII): N-Dimensional Vectors”): You can treat any place as the south pole, the direction along the Hopf fibration from there is the equator, and perpendicular to it is the north pole. On such a planet, both types of needles will point in the direction of Hopf fibers. If the current flow is the same as the planet’s rotation, then the planet performs isoclinic double rotation, and the needles point in the direction of the planet’s motion at that point. That is, the needles on an isoclinic double-rotating planet haven’t completely failed! They still preserve one direction to give explorers orientation hints! If the planet’s two loop currents are very close but still slightly different (99%), then east-west-south-north-yin-yang still have meaning, and the compass angle curve variation with latitude looks like this: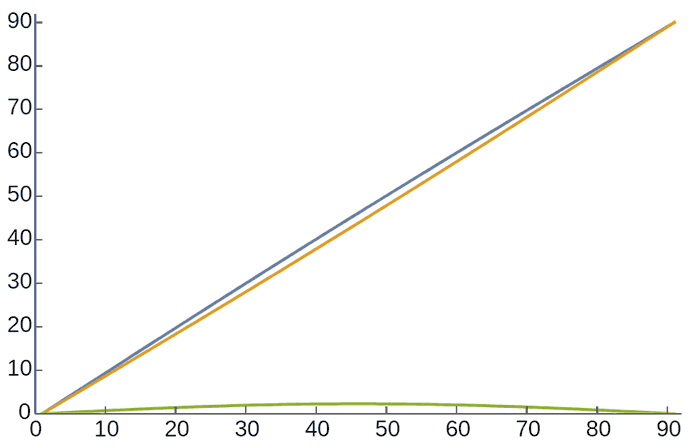
Self-Dual and Anti-Self-Dual Magnetic Dipoles
You might notice, why do we say point-south, point-east, point-yang compasses, not point-north, point-west, point-yin compasses? They’re just two ends of the needle anyway, so most of the time it doesn’t matter. However, when we weld the point-east and point-yang compasses together to evolve into a compound magnetic field compass, direction does matter, especially when the geomagnetic field is also compound. Let’s look at a more extreme example: a 4D planet’s geomagnetic field is a self-dual magnetic dipole. At this time, the magnetic field at any point on the planet is the same, and any point can be treated as the “south-north pole.” Due to the complete symmetry of the south-north poles, the horizontal component of the magnetic field at each point on this planet equals the vertical component. The point-east and point-yang compasses respectively sense the horizontal and vertical components, so the forces they experience are also the same. Explorers on such a planet would get the same result using either type of compass. This also explains from another angle why two needles would overlap on an isoclinic double-rotating planet. We can even bind the two compasses together completely overlapping with no angle between them (unlike the previously designed compass that required perpendicular welding). The resulting needle obviously points the same as individual point-yang or point-east compasses, but it has two absolutely perpendicular magnetization directions—the needle itself is also a self-dual-like magnetic dipole! But if we accidentally reverse the direction when binding the point-east and point-yang compasses (the point-yang compass becomes a point-yin compass), then the two components of the new needle experience equal and opposite torques at all times, resulting in zero net force and thus failure. This needle’s dipole and the magnetic dipole field from superposition in the same direction are mirror images of each other—you can understand self-dual as loop current from west to east plus from yin to yang, while anti-self-dual is loop current from west to east plus from yang to yin. There’s a classic conclusion in 4D magnetostatics: if we consider self-dual and anti-self-dual magnetic dipoles as two types of “magnetism,” then opposite types attract each other, but same types neither attract nor repel—there’s no interaction force between them at all!
Using Coriolis Force for Navigation
Are there other means to help explorers determine direction? We know that in Earth’s northern hemisphere, water draining from a sink swirls counterclockwise, and the opposite in the southern hemisphere. This is due to the deflection force produced by Earth’s rotation. What’s the situation on a 4D planet? Can it help us find direction?
To answer these questions, let’s first look at the inertial forces experienced by objects in a rotating reference frame in 3D space. Objects will experience two types of inertial forces: the first is centrifugal force, and the second is this deflection force (also called Coriolis force). We focus on the second type of force. The Coriolis force entry on Wikipedia has a gif animation that clearly shows the essence of this deflection force: Since uniform linear motion of an object not subject to forces is no longer straight in a rotating reference frame, a virtual inertial force needs to be introduced to make the object deviate from the straight direction.
Note that this force is perpendicular to the object’s direction of motion, so it doesn’t change the speed magnitude. Doesn’t it seem a bit like the Lorentz force in a magnetic field? Actually, the first type of inertial force is like electric field force, and the second type is like magnetic field force. In general relativity, there’s something called gravitoelectromagnetism as a linear approximation…
Back to the water vortex. Similar to the compass situation, water flow on the rotating equator experiences Coriolis force in the vertical direction, but this deflection force is very weak and cannot compete with gravity to produce observable effects. Therefore, only the components of Earth’s rotational angular velocity on the 3D ground surface $e_{xy},e_{xz},e_{yz}$ affect the fluid. Since 2-vectors in 3D space are all simple, we can always find an axis that doesn’t participate in rotation. Water flow in the axis direction won’t experience deflection force and will flow straight into the drain, while water around the axis will form a tornado-like structure under the deflection force.
Explorers can get a clear direction by applying the standard right-hand rule in 3D ground space through the tornado direction. If the geomagnetic field is completely consistent in size and direction proportionally with the rotational angular velocity field, then this water vortex direction “compass” is the same as the second type of yin-yang compass. However, this means it has all the disadvantages of the point-yang compass, including equator failure, double-rotation planet errors, etc. Note that planetary rotation can be viewed as a rigid body with a uniform angular velocity field, while the geomagnetic field is a dipole field. Although their horizontal and vertical component variation trends are similar, angle deviations and failures will occur, but the variation directions of horizontal and vertical components are opposite, and the specific deviation calculation and correction methods are completely different. However, based on Coriolis force, we can only make a point-yang compass, with no chance to compare angles with a non-existent point-east compass…
Finally, let’s see what our water vortex point-yang compass becomes when reduced to 3D Earth. Earth only rotates from west to east in a single rotation. Since there’s no yin-yang direction on a 2D sphere, the water vortex pointing yin-yang degenerates into two types of point vortices—counterclockwise and clockwise. Using it, we can only distinguish whether we’re in the northern or southern hemisphere.
Using the Starry Sky for Navigation
The ancient sages of the 4D world have long had deep research in astronomy. Although the stars in the sky are much sparser than on Earth (caused by the instability of orbits due to the inverse cube law), finding directions through star charts still has certain reference value. By observing the trajectories of specific stars in the sky, we can reflect the planet’s rotation and thus calculate the latitude. Are there stars on a 4D planet similar to Polaris that you can walk straight toward to reach a fixed position? The main problem with 4D planets is they don’t have a rotation axis, only a rotation plane. If it’s a single-rotation planet, we can find the non-rotating equator. All stars above that circle are stationary relative to the ground. Assuming single rotation from west to east, the non-rotating equator is the yin-yang equator. As long as we mark these stars in advance, by recognizing and walking toward a certain star, we can directly arrive at a given longitude position on the yin-yang equator. If your destination isn’t polar, you can’t navigate by just one star—the line connecting all stars on the yin-yang equator seen from anywhere must also be parallel to the yin-yang direction. Actually, this also applies to double-rotation planets: stars will move along this line without hindering navigation. The same applies to the east-west direction—just recognize the circle of stars above the east-west equator and find the connecting line. This method even works on highly symmetric isoclinic double-rotation planets! As long as you remember the stars above specific equators, star charts will break the terrifying Hopf fibration symmetry of double rotation, so you won’t get lost! It seems that identifying directions through the starry sky is very efficient (who needs compasses!). As long as you can recognize a bunch of stars directly above two absolutely perpendicular equators, and also, don’t encounter cloudy weather (seems like we still can’t throw away the compass…)
Having figured out navigation methods on 4D planets, the explorer has compiled compass deviation correction tables and is ready to set off on a round-the-world adventure! What scenery will they see along the way? Stay tuned for the next episode!