Build Digital Circuits with Hutton32 (II): Logic Components

The previous article introduced how to build AND, OR, and NOT gates in Hutton32. Now let’s use their combinations to do some interesting things. (Like a perfect square calculator!)

XOR, XNOR Gates

A XOR B means that the output is 1 if the inputs are different, and 0 if they are the same. The logical expression is (A & ~B) | (~A & B). But note that this requires two NOT gates, and NOT gates are large and have long delays, so we simplify the expression to get an XOR gate with only one NOT gate: (A | B) & ~(A & B); XNOR is similar: ~(A | B) | (A & B).

With basic logic gates, we can create various combinational logic and sequential logic circuits! Here are some components I’ve made:

Latch

A latch requires two NOT gates. To reduce delay, we use discrete signals directly inside, because NOT gates must have discrete signals.
RS Latch:

A storage unit composed of D latches: (R, W are read and write enable terminals)

Adder/Subtractor

The schematic for an adder is widely available online. Subtraction is done by inverting (using a NOT gate) and then adding one (by providing a carry-in signal to the lowest bit of the adder).

Since all internal signals are continuous, the NOT gate requires conversion, which takes up a lot of space. I was too lazy to do discrete optimization (dealing with phases is too troublesome).

Counter

The counter here is not the kind found in general digital circuits. This is a very important component in Hutton32 used for frequency division or delay. CFY’s article has a detailed description of its principle.
Frequency division:

Single signal delay or generating a long pulse:

The long pulse is output from the top, and the delayed signal is output from the right. Changing the counter period can change the delay time, but make sure the phase remains consistent after the change! Otherwise, the signal generator cannot be turned off correctly.

Binary to BCD Decoder

Digital circuits operate in binary, so to display in decimal, a binary to BCD decoder is necessary. I found a construction method in a redstone tutorial on a Minecraft forum. The core of the algorithm is the Double Dabble algorithm, which can be found in the link to the redstone tutorial above.
First, we need to create a basic component called a plus-three-when-greater-than-five adder (P3GT5 adder), which takes a 4-bit binary number as input. If the number is greater than or equal to 5, it adds three (and also outputs a 4-bit number, ignoring the carry); otherwise, it remains unchanged: y = ( x >= 5 ) ? x+3 : x;. To build this part, we first need to detect if it’s greater than 5 and also have an adder. I ended up using 5 NOT gates to implement the entire component.

Then we continuously copy this P3GT5 adder as a whole. In fact, this machine runs very slowly and is huge. We can optimize it by using all discrete signals, because NOT gates must have discrete signals, and we just need to convert the signals at the input and output. But this is very sensitive to phase. So we need to ensure the entire system works at the same phase, which is a test of wiring. If the phase is out of sync, we can use a one-in-one-out diamond delay to compensate for the phase.
I was originally lazy and didn’t want to use discrete signals because I would have to adjust the phase, but the P3GT5 adder is a basic unit, and to get the final decoder, we have to copy and paste these units, so improving its performance is necessary. The discrete version of the P3GT5 adder is as follows:

The final product after copying and pasting:

This is a 16-bit binary to BCD converter, using a total of 35 P3GT5 adders.

Perfect Square Display

Although with our current knowledge we still can’t build a prime number calculator, a perfect square calculator is now possible. Calculating perfect squares doesn’t require a multiplier, because the sequence 1, 4, 9, 16, 25… can be seen as the sum of the arithmetic sequence 1, 3, 5, 7, 9… The following is a block diagram of a perfect square calculator: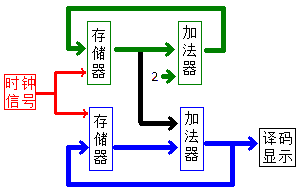
Here, the green memory unit has an initial value of 1, and the blue one has an initial value of 0. The clock controls the write operation. (The memory units are always in a readable state.) The final decoding part converts the binary to BCD using a binary to BCD converter, and then displays it using a 7-segment decoder.

The finished product I made:

Getting to this point means we’re not far from a calculator! To make a calculator, we still need one more component: a BCD to binary converter. We humans input decimal numbers, so we need a part that converts decimal to binary. We can do this in reverse: create an ‘’’inverse P3GT5 adder’’’:

Input	P3GT5 adder	Inverse P3GT5 adder
0	0	0/13
1	1	1/14
2	2	2/15
3	3	3
4	4	4
5	8	x
6	9	x
7	10	x
8	11	5
…	…	…
12	15	9
13	0	10
14	1	11
15	2	12

Doing it in reverse has a problem: the inverse P3GT5 adder has a one-to-many state (0/1/2 could correspond to 0/1/2 or to 13/14/15), which seems impossible to reverse. But fortunately, it has been proven that states like 13/14/15 will not appear, so we can boldly assume that 0/1/2 corresponds to 0/1/2. Thus, the inverse P3GT5 adder is a minus-three-when-greater-than-eight adder.
I have only made the continuous version of the minus-three-when-greater-than-eight adder. I haven’t done the discrete optimization yet. (Because I have my final exam for digital circuits tomorrow, I still need to review…).